Università degli Studi di Bergamo — Facoltà di Ingegneria
Matematica I — Appello del 2 Luglio 2007 – Tema A
Matr.
Cognome e Nome
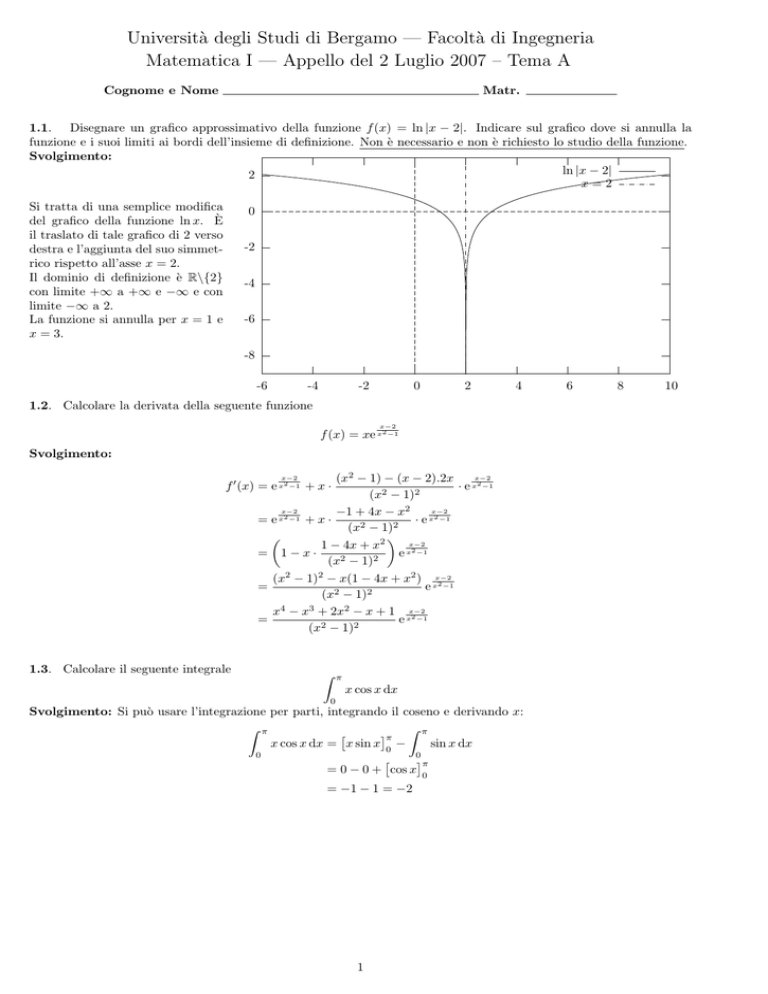
1.1. Disegnare un grafico approssimativo della funzione f (x) = ln |x − 2|. Indicare sul grafico dove si annulla la
funzione e i suoi limiti ai bordi dell’insieme di definizione. Non è necessario e non è richiesto lo studio della funzione.
Svolgimento:
ln |x − 2|
2
x=2
Si tratta di una semplice modifica
del grafico della funzione ln x. È
il traslato di tale grafico di 2 verso
destra e l’aggiunta del suo simmetrico rispetto all’asse x = 2.
Il dominio di definizione è R\{2}
con limite +∞ a +∞ e −∞ e con
limite −∞ a 2.
La funzione si annulla per x = 1 e
x = 3.
0
-2
-4
-6
-8
-6
-4
-2
0
2
4
1.2. Calcolare la derivata della seguente funzione
x−2
f (x) = xe x2 −1
Svolgimento:
(x2 − 1) − (x − 2).2x xx−2
· e 2 −1
(x2 − 1)2
x−2
−1 + 4x − x2 xx−2
= e x2 −1 + x ·
· e 2 −1
(x2 − 1)2
x−2
1 − 4x + x2
= 1−x·
e x2 −1
2
2
(x − 1)
2
2
(x − 1) − x(1 − 4x + x2 ) xx−2
=
e 2 −1
(x2 − 1)2
x4 − x3 + 2x2 − x + 1 xx−2
=
e 2 −1
(x2 − 1)2
x−2
f 0 (x) = e x2 −1 + x ·
1.3. Calcolare il seguente integrale
Z
π
x cos x dx
0
Svolgimento: Si può usare l’integrazione per parti, integrando il coseno e derivando x:
Z π
Z π
π
x cos x dx = x sin x 0 −
sin x dx
0
0
π
= 0 − 0 + cos x 0
= −1 − 1 = −2
1
6
8
10
1.4. Risolvere il seguente problema di Cauchy
(
y0
= 2x(1 − y 2 )
y(0) = 1
Svolgimento: Si tratta di un’equazione differenziale a variabili separabili. Le soluzioni costanti sono quelle per cui
y = ±1. In particolare, siccome il dato iniziale è y(0) = 1, la soluzione del problema di Cauchy è la soluzione costante
y = 1.
1.5. Stabilire il carattere della serie
+∞
X
(−1)n
√
n+ n
n=1
Svolgimento: Si tratta di una serie a termini alterni: n+1√n è positivo per ogni n ma (−1)n cambia segno (è positivo,
uguale a 1 per n pari e negativo,
uguale a −1 per n dispari).
√
√
Le due successioni n e n sono crescenti, quindi n + n è crescente e quindi n+1√n è una successione decrescente.
Il limite di questa successione è 0 (perché è il rapporto di una successione costante per una successione che tende
all’infinito). Dal criterio di Leibniz vediamo che la serie è convergente.
1.6. Risolvere la seguente disequazione:
√
x−26x+3
Svolgimento: Le soluzioni della disequazione devono verificare x > 2, se no la radice quadrata non è definita. Per
x > 2 il termine x + 3 è certamente positivo. Possiamo elevare al quadrato ottenendo
x − 2 6 (x + 3)2 = x2 + 6x + 9 ⇐⇒ 0 6 x2 + 5x + 11.
Il discriminante del polinomio è ∆ = 25 − 44 = −19 < 0, quindi l’ultima disuguaglianza è sempre verificata.
L’insieme delle soluzioni è {x|x > 2} = [2; +∞).
2
2.1. Studiare la funzione
f (x) = ln(5e2x − 4ex − 1) − 2x
e tracciarne un grafico qualitativo
Dominio, segno, eventuali simmetrie, limiti ai bordi del dominio ed eventuali asintoti: La funzione è
definita per ogni x tale che 5e2x − 4ex − 1 = 5(ex )2 − 4ex − 1 > 0. Il trinomio 5t2 − 4t − 1 è positivo per t < − 51 e t > 1
e quindi (siccome t = ex > 0), la funzione è definita per x > 0.
La funzione non presenta simmetrie.
2x
x
−1
= ln(5 − 4e−x − e−2x )
Siccome limx→0 5e2x − 4ex − 1 = 0, limx→0+ f (x) = −∞. Osserviamo che f (x) = ln 5e −4e
e2x
e quindi limx→+∞ f (x) = ln 5. Abbiamo quindi un asintoto verticale in x = 0 e uno orizontale verso +∞.
La funzione è √
positiva quando 5 − 4ex − e−2x > 1, √
cioè quando e−2x + 4ex √
− 4 < 0. Il trinomio t2 + 4t − 4 si√annulla
−x
per x > − ln(2 2 − 2).
in t = −2 ± 2 2. Quindi f è negativa per e > 2 2 − 2, cioè x < − ln(2 2 − 2) e positiva
√
√
√
√
1+
2
1
(Oss: − ln(2 2 − 2) = − ln( 2 − 1) − ln 2 = ln √2−1 − ln 2 = ln( 2 + 1) − ln 2 = ln 2 > 0).
Derivata prima:
10e2x − 4ex
10e2x − 4ex − 10e2x + 8ex + 2
−
2
=
5e2x − 4ex − 1
5e2x − 4ex − 1
4ex + 2
2ex + 1
= 2x
= 2 2x
5e − 4ex − 1
5e − 4ex − 1
Crescere e decrescere, massimi, minimi: Il numeratore di f 0 (x) è ovviamente positivo, abbiamo già visto che il
denominatore è positivo sull’insieme di definizione di f , quindi f 0 (x) è positiva sull’insieme di definizione di f e quindi
f è strettamente crescente. Non si sono quindi né massimi né minimi, né locali né globali.
f 0 (x) =
Derivata seconda:
10e3x − 8e2x − 2ex − 20e3x + 8e2x − 10e2x + 4ex
2ex (5e2x − 4ex − 1) − (2ex + 1)(10e2x − 4ex )
=2
2x
x
2
(5e − 4e − 1)
(5e2x − 4ex − 1)2
−10e3x − 10e2x + 2ex
5e2x + 5ex − 1
=2
= −4ex
2x
x
2
(5e − 4e − 1)
(5e2x − 4ex − 1)2
f 00 (x) = 2
Concavità e convessità:
Le radici di 5t2 + 5t − 1 sono
quindi ∀x > 0, f 00 (x) < 0. La funzione è concava.
√
−5 ± 3 5
e per t = ex > 1, abbiamo 5t2 + 5t − 1 > 0 e
10
Grafico:
2
ln(5e2x − 4ex − 1) − 2x
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-1
0
1
2
3
3
4
5
2.2. Stabilire per quali valori dei parametri reali a e b è possibile applicare nell’intervallo [−1, 1] il teorema di Lagrange
alla funzione
(
(x − 1)(x + a) per x 6 0
f (x) =
ln(1+bx)
per x > 0
x
Svolgimento: Per poter applicare il teorema di Lagrange, la funzione f deve essere continua su [−1, 1] e derivabile su
(−1, 1). Per x < 0 la funzione è ovviamente continua e derivabile. Per x > 0 è continua e derivabile, purché 1 + bx sia
positivo sur tutto l’intervallo considerato; perché questa condizione sia verificata sull’intervallo (0; 1], dobbiamo avere
b > −1. Il problema sta in 0: secondo i valori di a o di b, la funzione potrebbe essere discontinua o non derivabile.
Per x < 0, abbiamo f (x) = (x − 1)(x + a), quindi f 0 (x) = x + a + x − 1 = 2x + a − 1. Quindi
lim f (x) = −a
x→0−
Per x > 0, abbiamo f (x) =
lim f 0 (x) = a − 1 = f 0 (0− ).
x→0−
ln(1 + bx)
, quindi
x
lim f (x) = lim
x→0+
x→0+
ln(1 + bx)
ln(1 + bx)
= lim b
= b.1 = b.
+
x
bx
x→0
Invece
ln(1+bx)
x
f (x) − f (0)
f (0 ) = lim+
= lim+
x
x→0
x→0
0
+
−b
x
= lim+
x→0
ln(1 + bx) − bx
x2
(bx)2
2
+ (bx)2 ε(x) − bx
b2
b2
= lim+ − + b2 ε(x) = − .
2
x
2
2
x→0
x→0
√
2
Quindi dobbiamo avere −a = b e a − 1 = − b2 , cioè a2 + 2a − 2 = 0 che ammette a = −1 ± 2 e b = −a. Nei due casi
√
√
√
√
b > −1 quindi ci sono due soluzioni: a = −1 + 2, b = 1 − 2 e a = −1 − 2, b = 1 + 2.
= lim+
bx −
2.3. Risolvere il seguente problema di Cauchy:
(
y 0 − y cot x = 2x sin x
y( π2 ) = 1
Svolgimento: Si tratta di un’equazione differenziale lineare. Cominciamo dal risolvere l’equazione omogenea corx
rispondente, cioè y 0 − y cot x = 0 o y 0 = y cos
sin x . Questa equazione è un’equazione a variabili separabili, la cui unica
soluzione costante è y = 0. Per y 6= 0, abbiamo
y0
cos x
=
y
sin x
⇐⇒
dy
cos x dx
=
y
sin x
e quindi ln |y| = ln | sin x| + C con C ∈ R. Quindi |y| = eC | sin x|, cioè y = K sin x con K = ±eC (K = eC se y e sin x
hanno lo stesso segno e K = −eC se y e sin x hanno segni opposti). Si ritrova la soluzione costante per K = 0.
Per risolvere l’equazione completa, usiamo il metodo della variazione della costante arbitraria. Cerchiamo una funzione
(derivabile) k tale che y = k(x) sin x sia soluzione dell’equazione differenziale. Allora y 0 = k 0 (x) sin x + k(x) cos x e
quindi y 0 − y cot x = k 0 (x) sin x + k(x) cos(x) − k(x) cos x = k 0 (x) sin x. La funzione k deve quindi verificare k 0 (x) = 2x,
cioè k(x) = x2 + C, con C ∈ R.
Le soluzioni dell’equazione differenziale sono quindi della forma y(x) = (x2 + C) sin x, con C ∈ R. Nel nostro caso in
2
x = π2 abbiamo y = 1 e quindi C = 1 − π4 .
Soluzione: y = x2 + 1 −
π2
4
sin x.
4
Università degli Studi di Bergamo — Facoltà di Ingegneria
Matematica I — Appello del 2 Luglio 2007 – Tema B
Matr.
Cognome e Nome
p
1.1. Disegnare un grafico approssimativo della funzione f (x) = |x + 1|. Indicare sul grafico dove si annulla la
funzione e i valori massimi e minimi che raggiunge. Non è necessario e non è richiesto lo studio della funzione.
Svolgimento:
2
p
|x + 1|
x = −1
1.5
Si tratta di una semplice modifica
√
del grafico della funzione x. È
il traslato di tale grafico di 1 verso
1
sinistra e l’aggiunta del simmetrico
di tale grafico rispetto alla retta
x = −1.
0.5
La funzione si annulla per x = −1
e tende a +∞ a +∞ e −∞.
0
-0.5
-3
-2.5
-2
f (x) =
-1.5
-1
-0.5
1.2. Calcolare la derivata della seguente funzione
1
ln
x−1
x+1
Svolgimento:
x+1−(x−1)
(x+1)2
f 0 (x) = − ln
x−1
x+1
x+1
· x−1
2
2
(x+1)(x−1)
= − 2
ln x−1
x+1
2
=−
(x2 − 1) ln
1.3. Calcolare il seguente integrale
Z
0
Svolgimento:
Z
0
π
4
sin x
dx =
cos2 x
Z
0
π
4
x−1
x+1
π
4
2 =
2
(1 − x2 ) ln
x−1
x+1
2
sin x
dx
cos2 x
π4
1
1 √
− sin x
1
−
dx =
= 1 − = 2 − 1.
2
√
cos x
cos x 0
1
2
1
0
0.5
1
1.4. Risolvere il seguente problema di Cauchy
(
y0
= tan y
y(1) = π
Svolgimento: Si tratta di un’equazione a variabili separabili. Le soluzioni costanti sono della forma y = kπ, con
k ∈ Z. La soluzione del problema di Cauchy è quindi
y(x) = π.
+∞ 2
X
n +1
n!
n=1
Svolgimento: Si tratta di una serie a termini positivi. Possiamo usare il criterio del rapporto:
1.5. Stabilire il carattere della serie
(n+1)2 +1
(n+1)!
n2 +1
n!
=
1 + n2 + n22
n!
1
n2 + 2n + 2
1
(n + 1)2 + 1
·
=
·
=
·
2
2
n +1
(n + 1)!
n+1
n +1
n+1
1 + n12
Siccome il limite è 0 < 1, la serie converge.
1.6. Risolvere la seguente disequazione:
√
x+2>x−2
Svolgimento: Le soluzioni della disequazione devono verificare x > −2, se no la radice quadrata non è definita.
Se −2 6 x 6 2, x − 2 6 0 e quindi la disequazione è verificata.
Se x > 2, abbiamo x − 2 > 0 quindi la disequazione è verificata se e solo se x + 2√> (x − 2)2 = √
x2 − 4x + 4, cioè se e
5−
17
5+
solo se x2 − 5x + 2 6 0. L’equazione x2 − 5x + 2 = 0 ha due soluzioni: x1 = 2
e x2 = 2 17 . Abbiamo quindi
√
x2 − 5x + 2 6 0 per x1 6 x 6 x2 . Siccome 16 < 17, 4 < 17 e quindi x1 < 21 e x2 > 92 . Quindi abbiamo x > 2 e
x2 − 5x + 2 6 0 per 2 < x 6 x2 .
h
√
√ i
L’insieme delle soluzioni è {x| − 2 6 x 6 5+2 17 } = −2; 5+2 17 .
2
2.1. Studiare la funzione
√
f (x) = x 3 x − 2
e tracciarne un grafico qualitativo
Dominio, segno, eventuali simmetrie, limiti ai bordi del dominio ed eventuali asintoti: La funzione è
definita su tutto R, non ha simmetrie e il limite a ±∞ è +∞.
La funzione si annulla per x = 0 e x = 2, ha il segno di x(x − 2) e quindi è positiva su (−∞; 0) ∪ (2; +∞) e negativa
su (0; 2).
√
3
x − 2 per cui il limite di f (x)
Abbiamo f (x)
x =
x a ±∞ è infinito e quindi non ci sono asintoti.
√
Derivata prima: In x = 2 la funzione è asintotica a 2 3 x − 2 e quindi non è derivabile. Per x 6= 2, abbiamo
√
3
3(x − 2) + x
1
x
p
= p
3
2
3 (x − 2)
3 3 (x − 2)2
4x − 6
2(2x − 3)
= p
= p
3 3 (x − 2)2
3 3 (x − 2)2
f 0 (x) =
x−2+
Crescere e decrescere, massimi, minimi: La derivata di f ha il segno di 2x − 3, quindi è negativa per x < 32
e positiva per x > 23 . Quindi f è decrescente su (−∞; 32 ) e crescente su ( 32 ; +∞). In x = 32 , f raggiunge un minimo
3
uguale a − 2 √
3 .
2
Derivata seconda: Per x 6= 2,
p
2 3 (x − 2)2 − (2x − 3) 23 ·
2
p
f 00 (x) = ·
3
3
(x − 2)4
=
p
3 3 (x − 2)2 − (2x − 3) ·
4
p
= ·
3
9
(x − 2)4
x−3
1
1
1
(x−2) 3
(x−2) 3
1
4 3(x − 2) − (2x − 3)
4
p
= · p
·
3
5
9
9 3 (x − 2)5
(x − 2)
Concavità e convessità: La derivata seconda di f ha il segno di (x − 2)(x − 3), quindi è positiva per x < 2 e x > 3
e negativa per 2 < x < 3. La funzione è quindi convessa per x < 2 e x > 3 e concava per 2 < x < 3. (Il cambiamento
di concavità in x = 2 si fa tramite una tangente verticale).
Grafico:
6
√
x3x−2
5
4
3
2
1
0
-1
-2
-2
-1
0
1
2
3
3
4
2.2. Stabilire per quali valori dei parametri reali a e b è possibile applicare nell’intervallo [−1, 1] il teorema di Lagrange
alla funzione
(
(x + 21 )(x + a) per x 6 0
f (x) =
ln(1+bx)
per x > 0
x
Svolgimento: Per poter applicare il teorema di Lagrange, la funzione f deve essere continua su [−1, 1] e derivabile su
(−1, 1). Per x < 0 la funzione è ovviamente continua e derivabile. Per x > 0 è continua e derivabile, purché 1 + bx sia
positivo sur tutto l’intervallo considerato; perché questa condizione sia verificata sull’intervallo (0; 1], dobbiamo avere
b > −1. Il problema sta in 0: secondo i valori di a o di b, la funzione potrebbe essere discontinua o non derivabile.
Per x < 0, abbiamo f (x) = (x + 21 )(x + a), quindi f 0 (x) = x + a + x + 12 = 2x + a + 21 . Quindi
a
2
lim f (x) =
x→0−
Per x > 0, abbiamo f (x) =
lim f 0 (x) = a +
x→0−
1
= f 0 (0− ).
2
ln(1 + bx)
, quindi
x
lim f (x) = lim
x→0+
x→0+
ln(1 + bx)
ln(1 + bx)
= lim b
= b.1 = b.
x
bx
x→0+
Invece
f 0 (0+ ) = lim
x→0+
f (x) − f (0)
= lim
x
x→0+
(bx)2
2
ln(1+bx)
x
x
−b
= lim
x→0+
ln(1 + bx) − bx
x2
2
+ (bx) ε(x) − bx
b2
b2
2
=
lim
−
+
b
ε(x)
=
−
.
x2
2
2
x→0
x→0+
√
2
Dobbiamo quindi avere a2 = b e a + 12 = − b2 , quindi a2 + 8a + 4 = 0, cioè a = −4 ± 2 3. Nei due casi b > −1, quindi
√
√
√
√
le soluzioni sono a = −4 − 2 3, b = 2 + 3 e a = −4 + 2 3, b = 2 − 3.
= lim+
bx −
2.3. Risolvere il seguente problema di Cauchy:
(
y 0 − y tan x = 2x cos x
y(0) = 1
Svolgimento: Si tratta di un’equazione differenziale lineare. Cominciamo dal risolvere l’equazione omogenea corsin x
rispondente, cioè y 0 − y tan x = 0 o y 0 = y cos
x . Questa equazione è un’equazione a variabili separabili, la cui unica
soluzione costante è y = 0. Per y 6= 0, abbiamo
sin x
y0
=
y
cos x
⇐⇒
dy
sin x dx
=
y
cos x
C
e
K
C
C
e quindi ln |y| = − ln | cos x| + C con C ∈ R. Quindi |y| = | cos
x| , cioè y = cos x con K = ±e (K = e se y e cos x
hanno lo stesso segno e K = −eC se y e cos x hanno segni opposti). Si ritrova la soluzione costante per K = 0.
Per risolvere l’equazione completa, usiamo il metodo della variazione della costante arbitraria. Cerchiamo una funzione
k(x)
k0 (x)
k(x) sin x
0
(derivabile) k tale che y = cos
e quindi y 0 −
x sia soluzione dell’equazione differenziale. Allora y = cos x + cos2 x
0
0
k(x) sin x
k(x) sin x
k (x)
0
2
y tan x = kcos(x)
x + cos2 x − cos2 x = cos x . La funzione k deve quindi verificare k (x) = 2x cos x = x(cos 2x + 1), cioè
2
k(x) = x2 sin 2x + cos 2x + x2 + C, con C ∈ R.
Le soluzioni dell’equazione differenziale sono quindi della forma y(x) =
caso in x = 0 abbiamo y = 1 e quindi C = −1.
Soluzione: y(x) =
x
2
sin 2x + cos 2x +
cos x
x2
2
−1
.
4
x
2
2
sin 2x+cos 2x+ x2 +C
,
cos x
con C ∈ R. Nel nostro
Università degli Studi di Bergamo — Facoltà di Ingegneria
Matematica I — Appello del 2 Luglio 2007 – Tema C
Matr.
Cognome e Nome
1
1.1. Disegnare un grafico approssimativo della funzione f (x) = (x + 1) 3 . Indicare sul grafico dove si annulla la
funzione e i suoi limiti ai bordi dell’insieme di definizione. Non è necessario e non è richiesto lo studio della funzione.
Svolgimento:
1.5
1
(x + 1) 3
x = −1
1
Si tratta di una semplice modifica
√
del grafico della funzione 3 x. È
0.5
la traslazione di 1 verso sinistra di
tale grafico.
Il dominio di definizione è R e
0
la funzione ammette limite +∞ a
+∞ e −∞ a −∞.
-0.5
La funzione si annulla in x = −1
(e ha una tangente verticale in tal
punto).
-1
-1.5
-3
-2.5
-2
-1.5
-1
-0.5
0
1.2. Calcolare la derivata della seguente funzione
f (x) = arccos
x2 + x
x−1
2 √
√
+x Svolgimento: Per xx−1
< 1 (cioè, in pratica, per −1 − 2 < x < −1 + 2)
(2x+1)(x−1)−(x2 +x)
(x−1)2
0
f (x) = − r
1−
x2 +x
x−1
2
=−
(2x + 1)(x − 1) − (x2 + x)
2x2 + x − 2x − 1 − x2 − x
√
p
=−
|x − 1| x2 − 2x + 1 − x4 − 2x3 − x2
|x − 1| (x − 1)2 − (x2 + x)2
=−
x2 − 2x − 1
√
|x − 1| −x4 − 2x3 − 2x + 1
1.3. Calcolare il seguente integrale
Z
0
1
1
dx
ex + 1
Svolgimento:
Z
0
1
Z 1
1
1
e−x
dx
=
dx = − ln(1 + e−x ) 0
x
−x
e +1
0 1+e
= − ln(1 + e−1 ) + ln(1 + 1)
= ln 2 − ln(1 + e−1 )
1
0.5
1
1.4. Risolvere il seguente problema di Cauchy
(
y0
= (y + 1)2 cos x
y(0) = −1
Svolgimento: Si tratta di un’equazione a variabili separabili. L’unica soluzione costante è y = −1. La soluzione del
problema di Cauchy è quindi
y(x) = −1.
+∞
X
2n + 1
3n+1 − n
n=1
Svolgimento: Si tratta di una serie a termini positivi. Il termine generale è asintotico a
n
2n
1 2
.
=
3n+1
3 3
n
Siccome 23 < 1, la serie di termine generale 23
è una serie geometrica convergente, quindi la serie di termine generale
1.5. Stabilire il carattere della serie
1
3
2
3
n
converge e quindi, dal criterio del confonto asintotico, la serie proposta è convergente.
1.6. Risolvere la seguente disequazione:
√
2x + 3 6 x + 1
Svolgimento: Le soluzioni della disequazione devono verificare x > − 23 , se no la radice quadrata non è definita.
Per x < −1 abbiamo x + 1 < 0 e quindi la disequazione non è verificata.
Per x > −1 i due termini della disequazione sono non negativi e √
quindi essaÏ verificata se e solo se 2x + 3 6 (x + 1)2 =
2
2
x + 2x +
√1 cioè se e solo se x > 2. Questo e verificato per x 6 2 e x > 2, ma siccome siamo nel caso x > −1, solo
per x > 2.
√ √
L’insieme delle soluzioni è quindi: x|x > 2 =
2; +∞ .
2
2.1. Studiare la funzione
r
f (x) = −(x + 9)
1+
2
x
e tracciarne un grafico qualitativo
Dominio, segno, eventuali simmetrie, limiti ai bordi del dominio ed eventuali asintoti: Il domionio di
f è costituio dagli x tali che x 6= 0 e 1 + x2 > 0. Siccome 1 + x2 = x+2
x ha il segno di x(x + 2), il dominio di f è
(−∞; −2] ∪ (0; +∞).
Non ci sono simmetrie.
Siccome limx→±∞ 1 + x2 = 1, f (x) ∼ −x per x → ±∞ e quindi il limite di f a ±∞ è ∓∞.
q
q
q
1 − 1 − x2
2
2
q
=
−1
e
f
(x)
+
x
=
1
−
x
−
9
=
Abbiamo limx→±∞ f (x)
1
+
1
+
x
−
9
1 + x2 = − √2 2 −
x
x
x
1+ 1+ x
2
1+ 1+ x
q
9 1 + x2 e quindi limx→±∞ f (x) + x = −10. C’è quindi la retta y = −x − 10 come asintoto diagonale a ±∞.
Derivata prima:
r
− x22
2 x+9
2
x+9
f (x) = − 1 + −
=− 1+ + q
·q
x
2
x x2 1 + 2
1 + x2
x
x + 9 − x2 1 + x2
−x2 − x + 9
x2 + x − 9
x2 + x − 9
q
q
=
=
=− q
= −√
x4 + 2x3
x2 1 + x2
x2 1 + x2
x2 1 + x2
r
0
Crescere e decrescere,
massimi, minimi: La
derivata di f ha il segno
opposto di x2 + x − 9. Il trinomio x2 + x − 9
√
√
√
−1± 37
−1− 37
−1+ 37
si annulla per x =
. Siccome x1 =
< −2 e x2 =
> 0, la funzione è decrescente su (−∞; x1 ),
2
2
2
crescente su (x1 ; −2) e (0; x2 ) e decrescente su (x2 ; +∞).
Derivata seconda:
00
f (x) = −
=−
=−
√
2x3 +3x2
(2x + 1) x4 + 2x3 − (x2 + x − 9) √
x4 +2x3
x4 + 2x3
=−
(2x + 1)x3 (x + 2) − (x2 + x − 9)x2 (2x + 3)
3
(x4 + 2x3 ) 2
(2x + 1)(x4 + 2x3 ) − (x2 + x − 9)(2x3 + 3x2 )
=−
3
(x4 + 2x3 ) 2
x2 (2x + 1)(x2 + 2x) − (x2 + x − 9)(2x + 3)
3
(x4 + 2x3 ) 2
x2 2x3 + 4x2 + x2 + 2x − (2x3 + 3x2 + 2x2 + 3x − 18x − 27)
(x4 + 2x3 )
3
2
=−
x2 (27 + 17x)
3
(x4 + 2x3 ) 2
Concavità e convessità: Il segno di f 00 (x) è l’opposto di quello di 17x + 27. È quindi positiva per x <> −2 e
negativa per x > 0. La funzione è quindi convessa per x > −2 e concava per x > 0.
Grafico:
10
q
−(x + 9) 1 + x2
y = −x − 10
0
-10
-20
-30
-40
-50
-20
-10
0
10
3
20
30
2.2. Stabilire per quali valori dei parametri reali a e b è possibile applicare nell’intervallo [−1, 1] il teorema di Lagrange
alla funzione
(x + 1)(x + a) per x > 0
f (x) =
ebx − 1
per x < 0
x
Svolgimento: Per poter applicare il teorema di Lagrange, la funzione f deve essere continua su [−1, 1] e derivabile su
(−1, 1). Per x < 0 la funzione è ovviamente continua e derivabile. Per x > 0 è continua e derivabile, purché 1 + bx sia
positivo sur tutto l’intervallo considerato; perché questa condizione sia verificata sull’intervallo (0; 1], dobbiamo avere
b > −1. Il problema sta in 0: secondo i valori di a o di b, la funzione potrebbe essere discontinua o non derivabile.
Per x > 0, abbiamo f (x) = (x − 1)(x + a), quindi f 0 (x) = x + a + x − 1 = 2x + a − 1. Quindi
lim f (x) = −a
x→0−
Per x < 0, abbiamo f (x) =
lim f 0 (x) = a − 1 = f 0 (0− ).
x→0−
ebx − 1
, quindi
x
lim f (x) = lim
x→0+
x→0+
ebx − 1
ebx − 1
= lim b
= b.1 = b.
x
bx
x→0+
Invece
f (x) − f (0)
f (0 ) = lim
= lim
x
x→0+
x→0+
0
+
(bx)2
2
ebx −1
x
x
−b
= lim
x→0+
ebx − 1 − bx
x2
2
+ (bx) ε(x) − bx
b2
b2
= lim+ − + b2 ε(x) = − .
2
x
2
2
x→0
x→0
√
2
Quindi dobbiamo avere −a = b e a − 1 = − b2 , cioè a2 + 2a − 2 = 0 che ammette a = −1 ± 2 e b = −a. Nei due casi
√
√
√
√
b > −1 quindi ci sono due soluzioni: a = −1 + 2, b = 1 − 2 e a = −1 − 2, b = 1 + 2.
= lim+
bx −
2.3. Risolvere il seguente problema di Cauchy:
y 0 − 1 y = √ 4x
1−x2
1 − x2
y(0) = 3
Svolgimento: A causa della radice quadrata al denominatore, il valore di x è limitato all’intervallo (−1; 1).
Si tratta di un’equazione differenziale lineare. Cominciamo dal risolvere l’equazione omogenea corrispondente, cioè
1
1
0
y 0 − 1−x
2 y = 0 o y = 1−x2 y. Questa equazione è un’equazione a variabili separabili, la cui unica soluzione costante è
y = 0. Per y 6= 0, abbiamo
y0
1
1 1
1 1
dy
1 1
1 1
=
=
+
⇐⇒
=
+
dx
y
1 − x2
21−x 21+x
y
21−x 21+x
r
1+x e quindi ln |y| = − 21 ln |1 − x| + 12 ln |1 + x| + C = ln 1−x
+ C con C ∈ R. Siccome x ∈ (−1; 1), 1−x
1+x > 0 e quindi
q
q
q
1+x
1+x
1+x
+ C. Segue |y| = eC 1−x
, cioè y = K 1−x
con K = ±eC (K = eC se y è positivo e K = −eC se y
ln |y| = ln 1−x
è negativo). Si ritrova la soluzione costante per K = 0.
Per risolvere l’equazione completa, usiamo il metodo della variazione della costante arbitraria. Cerchiamo
una funzione
r
1
q
1
+
x
1−x2
0
1+x
0
q
(derivabile) k tale che y = k(x) 1−x sia soluzione dell’equazione differenziale. Allora y = k (x)
+ k(x)
1−x
1+x
1−x
q
1
1+x
4x
4
0
0
e quindi y 0 − 1−x
2 y = k (x)
1−x . La funzione k deve quindi verificare k (x) = 1+x = 4 − 1+x , cioè k(x) =
4x − 4 ln |1 + x| + C = 4x − 4 ln(1 + x) + C, con
qC ∈ R.
Nel nostro caso in x = 0 abbiamo y = 3 = k(0)
Soluzione: y(x) = (4x − ln(1 + x) + 3)
q
1+0
1−0
= k(0) e quindi k(0) = 3, che significa C = 3.
1+x
1−x .
4
Università degli Studi di Bergamo — Facoltà di Ingegneria
Matematica I — Appello del 2 Luglio 2007 – Tema D
Matr.
Cognome e Nome
1.1. Disegnare un grafico approssimativo della funzione f (x) = |ex − 1|. Indicare sul grafico dove si annulla la funzione
e i suoi limiti ai bordi dell’insieme di definizione. Non è necessario e non è richiesto lo studio della funzione.
Svolgimento:
4
|ex − 1|
3.5
Si tratta di una semplice modifica
del grafico della funzione ex . È il
traslato di tale grafico di 1 verso
il basso, e la simmetria della parte
sotto l’asse x rispetto a tale asse.
La funzione si annulla in x = 0.
Il dominio di definizione è R con
limite +∞ a +∞ e 1 a −∞.
3
2.5
2
1.5
1
0.5
0
-4
-3
-2
-1
0
1
1.2. Calcolare la derivata della seguente funzione
f (x) = tan
x+1
x2 − x
Svolgimento:
x2 − x − (2x − 1)(x + 1)
x+1
2
f (x) =
1 + tan
(x2 − x)2
x2 − x
2
2
x − x − 2x − 2x + x + 1
x+1
2
=
1 + tan
(x2 − x)2
x2 − x
2
−x − 2x + 1
x+1
=
1 + tan2
2
2
(x − x)
x2 − x
2
x + 2x − 1
x+1
2
=−
1 + tan
(x2 − x)2
x2 − x
0
1.3. Calcolare il seguente integrale
Z
1
0
1
dx
x2 + 2x + 2
Svolgimento:
Z
0
1
1
dx =
x2 + 2x + 2
Z
1
0
Z
1
dx
(x + 1)2 + 1
2
1
dt
2+1
t
1
2
= arctan t 1
=
= arctan 2 − arctan 1 = arctan 2 −
1
π
4
2
3
4
1.4. Risolvere il seguente problema di Cauchy
(
y0
= cos2 y sin x
y(1) =
π
2
Svolgimento: Si tratta di un’equazione a variabili separabili. Le soluzioni costanti sono della forma y =
k ∈ Z. Il dato iniziale è di questa forma (con k = 0) quindi la soluzione del problema di Cauchy è
y(x) =
π
2
+ kπ con
π
.
2
+∞
X
(−1)n (n + 1)
n
n n=1
Svolgimento: La successione (−1) n(n+1) non ha limite (in valore assoluto tende a 1 ma il segno è + per gli n pari e
− per gli n dispari). In particolare non tende a 0 e quindi la serie non è convergente.
1.5. Stabilire il carattere della serie
1.6. Risolvere la seguente disequazione:
p
x2 − 1 > x − 5
Svolgimento: Dobbiamo avere x > 1 o x 6 −1 perché la radice quadrata sia definita.
Se x 6 5, x − 5 6 0 e quindi la disequazione è verificata.
Se invece x > 5, i due lati della disequazione sono positivi e quindi la disequazione è verificata se e solo se x2 − 1 >
(x − 5)2 = x2 − 10x + 25, cioè se e solo se 10x > 24, cioè se e solo se x > 12
5 (quindi sempre perché siamo nel caso
x > 5).
L’insieme delle soluzioni è {x|x 6 −1 o x > 1} = (−∞; −1] ∪ [1; +∞).
2
2.1. Studiare la funzione
√
f (x) = (2 − x) 3 x
e tracciarne un grafico qualitativo
Dominio, segno, eventuali simmetrie, limiti ai bordi del dominio ed eventuali asintoti: Il dominio di f è
tutto R. Il segno di f (x) è quello di x(2 − x), cioè posiva per 0 < x < 2 e negativa per x < 0 o x > 2.
Non ci sono simmetrie.
√
2
3
x quindi limx→±∞ f (x)
Il limite di f (x) a ±∞ è −∞. Inoltre f (x)
x = x −1
x = ±∞ e quindi non ci sono asintoti a
±∞.
√
Derivata prima: In x = 0 abbiamo f (x) ∼ 2 3 x e quindi f non è derivabile in 0. Per x 6= 0, abbiamo
√
2−x
−3x + 2 − x
√
f 0 (x) = − 3 x + √
=
3
3
3 x2
3 x2
2(1 − 2x)
√
=
3
3 x2
Crescere e decrescere, massimi, minimi: Il segno di f 0 (x) è quello di 1 − 2x, cioè è positivo per x < 21 e negativo
per x > 12 , quindi la funzione è crescente su (−∞; 12 ) e decrescente su ( 12 ; +∞). La funzione raggiunge un massimo in
3
x = 12 , dove prende il valore 2 √
3 .
2
Derivata seconda: Per x 6= 0 abbiamo
√
3
−2 x2 − 32 ·
00
√
f (x) = 2
3
3 x4
1+x
= −4 √
3
9 x5
1−2x
1
x3
= −4
3x + (1 − 2x)
√
3
9 x5
Concavità e convessità: Il segno di f 00 (x) è quello opposto di x(1 + x), quindi è negativo per x < −1 e x > 0 e
positivo per −1 < x < 0. La funzione f è quindi concava per x < −1 e x > 0 e convessa per −1 < x < 0.
Grafico:
2
√
(2 − x) 3 x
0
-2
-4
-6
-8
-3
-2
-1
0
1
2
3
3
4
5
2.2. Stabilire per quali valori dei parametri reali a e b è possibile applicare nell’intervallo [−1, 1] il teorema di Lagrange
alla funzione
1
(x − 2 )(x + a) per x > 0
f (x) =
ebx − 1
per x < 0
x
Svolgimento: Per poter applicare il teorema di Lagrange, la funzione f deve essere continua su [−1, 1] e derivabile su
(−1, 1). Per x < 0 la funzione è ovviamente continua e derivabile. Per x > 0 è continua e derivabile, purché 1 + bx sia
positivo sur tutto l’intervallo considerato; perché questa condizione sia verificata sull’intervallo (0; 1], dobbiamo avere
b > −1. Il problema sta in 0: secondo i valori di a o di b, la funzione potrebbe essere discontinua o non derivabile.
Per x < 0, abbiamo f (x) = (x − 21 )(x + a), quindi f 0 (x) = x + a + x − 12 = 2x + a − 21 . Quindi
lim f (x) = −
x→0−
Per x > 0, abbiamo f (x) =
a
2
lim f 0 (x) = a −
x→0−
1
= f 0 (0− ).
2
ebx − 1
, quindi
x
lim+ f (x) = lim+
x→0
x→0
ebx − 1
ebx − 1
= lim+ b
= b.1 = b.
x
bx
x→0
Invece
f (x) − f (0)
f (0 ) = lim+
= lim+
x
x→0
x→0
0
+
(bx)2
2
ebx −1
x
x
−b
= lim+
x→0
ebx − 1 − bx
x2
2
+ (bx) ε(x) − bx
b2
b2
2
ε(x)
=
−
+
b
.
=
lim
−
x2
2
2
x→0
x→0+
√
√
2
Dobbiamo quindi avere − a2 = b e a − 21 = − b2 e quindi a2 + 8a − 4 = 0, cioè a = −4 ± 20 = −4 ± 2 5. Le due
√
√
√
√
soluzioni sono quindi a = −4 − 2 5, b = 2 + 5 e a = −4 + 2 5, b = 2 − 5.
= lim+
bx −
2.3. Risolvere il seguente problema di Cauchy:
y 0 − 2x y = 1
1 + x2
y(0) = 3
Svolgimento: Si tratta di un’equazione differenziale lineare. Cominciamo dal risolvere l’equazione omogenea cor2x
2x
0
rispondente, cioè y 0 − 1+x
2 y = 0 o y = 1+x2 y. Questa equazione è un’equazione a variabili separabili, la cui unica
soluzione costante è y = 0. Per y 6= 0, abbiamo
2x
y0
=
y
1 + x2
⇐⇒
dy
2x dx
=
y
1 + x2
e quindi ln |y| = ln |1 + x2 | + C = ln(1 + x2 ) + C con C ∈ R. Abbiamo quindi |y| = eC (1 + x2 ), cioè y = K(1 + x2 ) con
K = eC se y > 0 e K = −eC se y < 0. Ritroviamo la soluzione costante per K = 0.
Per risolvere l’equazione completa, usiamo il metodo della variazione della costante arbitraria. Cerchiamo una funzione
(derivabile) k tale che y = k(x)(1 + x2 ) sia soluzione dell’equazione differenziale. Allora y 0 = k 0 (x)(1 + x2 ) + 2xk(x) e
2x
0
2
0
2
0
2
quindi y 0 − 1+x
2 y = k (x)(1+x )+2xk(x)−2xk(x) = k (x)(1+x ). La funzione k deve quindi verificare k (x)(1+x ) = 1,
1
3
cioè k 0 (x) = 1+x
2 ovvero k(x) = arctan x + C, con C ∈ R. Siccome y(0) = 3, abbiamo k(0) = 1+02 = 3 e quindi C = 3.
Soluzione: y = (arctan x + 3)(1 + x2 ).
4