Esame di Stato Liceo Scientifico PNI
Prova di Matematica - Corso sperimentale PNI - 19 giugno 2014
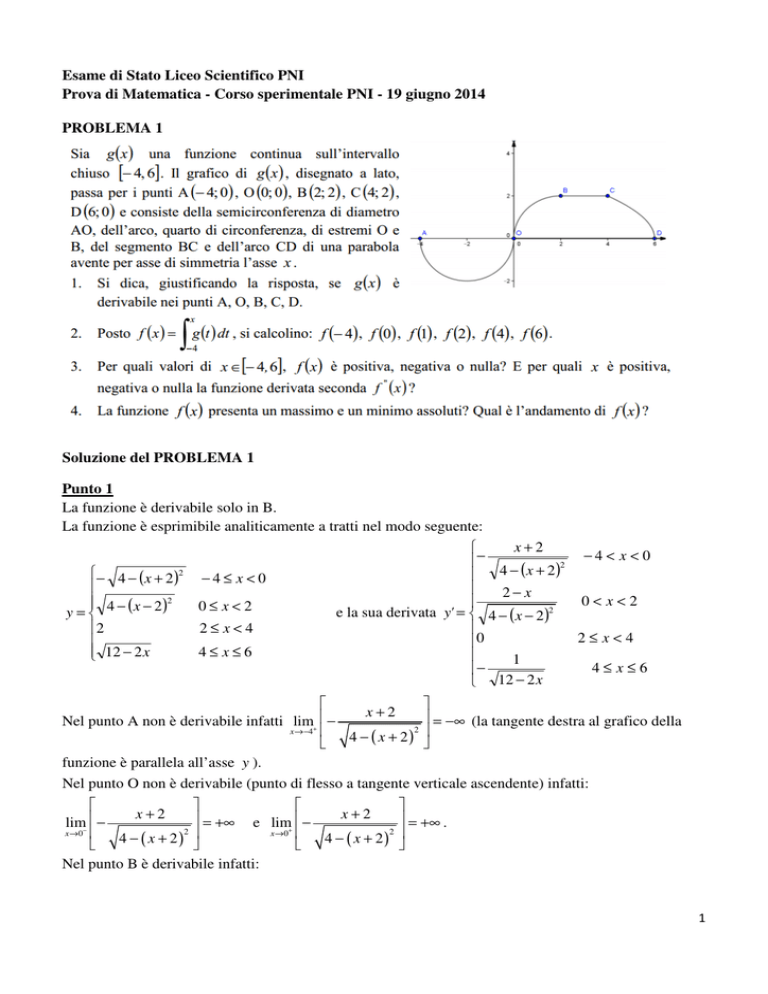
PROBLEMA 1
Soluzione del PROBLEMA 1
Punto 1
La funzione è derivabile solo in B.
La funzione è esprimibile analiticamente a tratti nel modo seguente:
− 4 − (x + 2 )2 − 4 ≤ x < 0
2
0≤ x<2
y = 4 − (x − 2)
2
2≤ x<4
4≤ x≤6
12 − 2 x
x+2
−4 < x < 0
−
2
(
)
4
−
x
+
2
2− x
0<x<2
e la sua derivata y' = 4 − ( x − 2 )2
2≤x<4
0
1
4≤ x≤6
−
12 − 2 x
x+2
= −∞ (la tangente destra al grafico della
Nel punto A non è derivabile infatti lim+ −
2
x →−4
4 − ( x + 2)
funzione è parallela all’asse y ).
Nel punto O non è derivabile (punto di flesso a tangente verticale ascendente) infatti:
x+2
x+2
lim− −
= +∞ e lim+ −
2
2
x →0
x →0
4 − ( x + 2)
4 − ( x + 2)
Nel punto B è derivabile infatti:
= +∞ .
1
2− x
= 0 e lim 0 = 0 .
lim
2
x→2+
x → 2−
4 − ( x − 2)
Nel punto C non è derivabile (punto angoloso) infatti:
1
1
e lim+ −
=−
x→4
2
12 − 2 x
lim− 0 = 0
x→4
1
Nel punto D non è derivabile infatti lim− −
= −∞ (la tangente sinistra al grafico della
x →6
12 − 2 x
funzione è parallela all’asse y ).
Punto 2
−4
f (− 4 ) =
∫ g (t )dt = 0
−4
0
f (0 ) = ∫ g (t )dt = −2π (opposto dell’area del semicerchio
−4
di centro (-2,0) e raggio 2)
1
2
3
4
3
=− π −
f (1) = ∫ g (t )dt = −2π + π −
2
3
2
−4
3
( f (0) + area settore circolare di angolo 60° privato del
triangolo rettangolo di cateti 1 e
(1, 3 )
3)
60°
1
2
f (2 ) = ∫ g (t )dt = −π
−4
( f (0) + area quarto di cerchio di centro (2,0) e raggio 2)
2
4
f (4 ) = ∫ g (t )dt = −π + 4
−4
( f (2) + area quadrato lato 2)
6
f (6 ) = ∫ g (t )dt = −π + 4 +
−4
8 20
=
−π
3 3
( f (4) + area metà segmento parabolico inscritto nel
rettangolo di dimensioni 4 e 2)
Punto 3
f (x ) = 0
per x = −4 ∨ x = 2 +
π
2
infatti per le considerazioni precedenti f (2) < 0 ∧ f (4) > 0 , f è continua, dunque f si annullerà in
corrispondenza di un valore α compreso tra 2 e 4 in modo tale che l’area del rettangolo di altezza 2 sia
pari a π essendo f (2) = −π ; tale rettangolo deve avere base
π
f (x ) > 0
per 2 +
f (x ) < 0
per − 4 < x < 2 +
2
π
2
, dunque α = 2 +
π
2
.
<x≤6
π
2
Per il teorema fondamentale del calcolo integrale f ' ( x ) = g ( x ) ∀x ∈ [− 4,6] , dal grafico di y = g ( x ) si
deduce che:
f ' ' ( x ) = 0 per x = −2 ∨ 2 ≤ x < 4
f ' ' (x ) > 0
per − 2 < x < 0 ∨ 0 < x < 2
f ' ' (x ) < 0
per − 4 < x < −2 ∨ 4 < x < 6
Punto 4
Riepilogando le considerazioni fatte in precedenza sulla funzione y = f ( x ) continua in [− 4,6] essa
ammette in tale intervallo massimo e minimo assoluti (per il Teorema di Weierstrass).
3
È decrescente in [− 4,0] , assume valore minimo assoluto in x = 0 e tale minimo vale − 2π ; poi è
crescente in [0,6] , si annulla in x = 2 +
π
ed è positiva in 2 + ,6 , assume valore massimo assoluto
2
2
π
20
−π .
3
Il grafico qualitativo della funzione f ( x ) è il seguente.
in x = 6 e tale massimo vale
Giudizio
Livello di difficoltà:
Basso
Medio
Alto
È in programma nel liceo
scientifico PNI?
Sì
No
Non si sa
Normalmente viene svolto?
Sì
No
Non sempre
È un argomento presente
nei libri di testo?
Mai
Non sempre
Sempre
Formulazione:
Scorretta
Controlla conoscenze/abilità/
competenze fondamentali?
Ambigua
Sì
Poco chiara
Corretta
Molto chiara
No
4












