Proposta programma delle PRIME e SECONDE SCIENZE

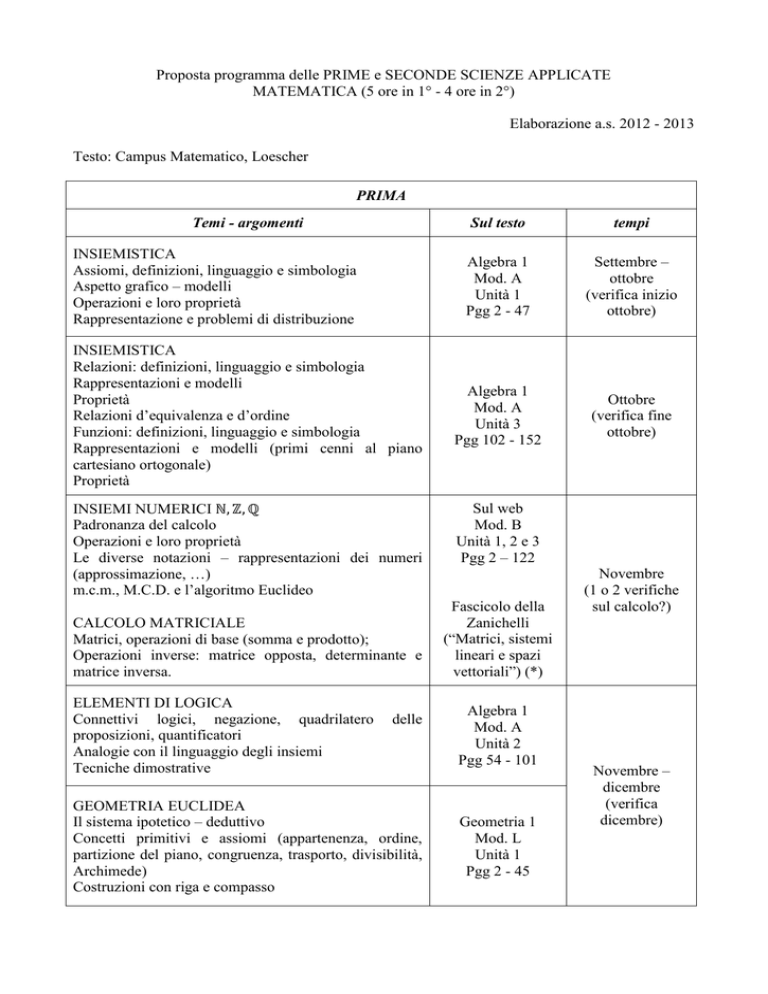
Proposta programma delle PRIME e SECONDE SCIENZE APPLICATE
MATEMATICA (5 ore in 1° - 4 ore in 2°)
Elaborazione a.s. 2012 - 2013
Testo: Campus Matematico, Loescher
PRIMA
Temi - argomenti
INSIEMISTICA
Assiomi, definizioni, linguaggio e simbologia
Aspetto grafico – modelli
Operazioni e loro proprietà
Rappresentazione e problemi di distribuzione
INSIEMISTICA
Relazioni: definizioni, linguaggio e simbologia
Rappresentazioni e modelli
Proprietà
Relazioni d’equivalenza e d’ordine
Funzioni: definizioni, linguaggio e simbologia
Rappresentazioni e modelli (primi cenni al piano
cartesiano ortogonale)
Proprietà
INSIEMI NUMERICI ℕ, ℤ, ℚ
Padronanza del calcolo
Operazioni e loro proprietà
Le diverse notazioni – rappresentazioni dei numeri
(approssimazione, …)
m.c.m., M.C.D. e l’algoritmo Euclideo
CALCOLO MATRICIALE
Matrici, operazioni di base (somma e prodotto);
Operazioni inverse: matrice opposta, determinante e
matrice inversa.
ELEMENTI DI LOGICA
Connettivi logici, negazione, quadrilatero
proposizioni, quantificatori
Analogie con il linguaggio degli insiemi
Tecniche dimostrative
delle
GEOMETRIA EUCLIDEA
Il sistema ipotetico – deduttivo
Concetti primitivi e assiomi (appartenenza, ordine,
partizione del piano, congruenza, trasporto, divisibilità,
Archimede)
Costruzioni con riga e compasso
Sul testo
tempi
Algebra 1
Mod. A
Unità 1
Pgg 2 - 47
Settembre –
ottobre
(verifica inizio
ottobre)
Algebra 1
Mod. A
Unità 3
Pgg 102 - 152
Ottobre
(verifica fine
ottobre)
Sul web
Mod. B
Unità 1, 2 e 3
Pgg 2 – 122
Fascicolo della
Zanichelli
(“Matrici, sistemi
lineari e spazi
vettoriali”) (*)
Algebra 1
Mod. A
Unità 2
Pgg 54 - 101
Geometria 1
Mod. L
Unità 1
Pgg 2 - 45
Novembre
(1 o 2 verifiche
sul calcolo?)
Novembre –
dicembre
(verifica
dicembre)
PRIMA
Temi - argomenti
Sul testo
tempi
CALCOLO LETTERALE
Monomi: definizioni, operazioni e proprietà
Polinomi: definizioni, operazioni e proprietà
Prodotti notevoli (con esercizi di applicazione “inversa”
tipo completamento o riconoscimento)
Divisione tra polinomi: regola generale, regola di
Ruffini, teorema del resto
Algebra 1
Mod. C
Unità 1 e 2
Pgg 160 - 254
Gennaio –
febbraio
(verifica inizio
febbraio)
EQUAZIONI e PROBLEMI di PRIMO GRADO
Definizioni, classificazione e soluzione delle equazioni
Impostazione di un problema
Problemi di primo grado
Algebra 1
Mod. D
Unità 1
Pgg 352 – 359
Pagg 366 – 377
Unità 2
Pgg 407 - 431
Febbraio
(verifica fine
febbraio)
GEOMETRIA EUCLIDEA
Triangoli e parallelismo – perpendicolarità
Criteri di congruenza dei triangoli, classificazione e
caratteristiche dei triangoli
Rette perpendicolari e triangoli rettangoli
Rette parallele, assioma di Euclide, criterio di
parallelismo
Geometria 1
Mod. L
Unità 2 e 3
Pgg 48 - 120
Marzo
(verifica)
CALCOLO LETTERALE
Scomposizione di polinomi (“semplici”)
Frazioni algebriche: semplificazione, operazioni ed
espressioni
Algebra 1
Mod. C
Unità 3 e 4
Pgg 258 - 350
EQUAZIONI (e problemi)
Equazioni di grado maggiore di 1 riconducibili a fattori
di primo grado
Equazioni fratte riconducibili a equazioni di primo
grado o a equazioni di grado maggiore di 1 riconducibili
a fattori di primo grado
Ampliamento conseguente della capacità di risolvere
problemi non lineari
Algebra 1
Mod. D
Unità1
Pgg 359 – 360
Pgg 363 – 365
Pgg 377 – 380
Pgg 402 - 406
GEOMETRIA EUCLIDEA
Quadrilateri e parallelogrammi
Corrispondenza e teorema di Talete
Luoghi geometrici e costruzioni con riga e compasso
Geometria 1
Mod. M
Unità 1 e 2
Pgg 122 - 175
Marzo - Aprile
(verifica fine
aprile oppure 2
verifiche separate)
Maggio
(verifica)
(*) Si può fare riferimento ad un fascicoletto della Zanichelli, “Matrici, sistemi lineari e spazi
vettoriali” di cui il Cavalleri possiede circa 200 copie, regalate dalla Zanichelli stessa, depositate in
Biblioteca nella sede di Parabiago. Il docente che intende svolgere tale argomento, si reca in
biblioteca (subito a sinistra entrando dalla porta che dà sul corridoio degli uffici), preleva il numero
di copie che gli servono, le distribuisce agli studenti (chiedendo di averne adeguata cura) e, finito
l’argomento (con relative verifiche e recuperi), riporta le copie dove le ha prese (trattenendo, se
interessato, una copia per sé). Predisporrò un apposito documento da compilare giusto per tenere un
minimo di controllo su questo materiale e per sapere chi l’ha prelevato. Il numero di copie dovrebbe
garantire la possibilità che si svolga tale argomento anche contemporaneamente in molte classi: se
non dovessero bastare, il documento su citato potrebbe servire per gestire ugualmente la situazione.
SECONDA
Temi - argomenti
Sul testo
tempi
RACCORDO col PROGRAMMA della PRIMA
 Ripasso
 Costruzioni con riga e compasso (magari virtuali)
 Luoghi geometrici (asse del segmento e bisettrice di
un angolo)
 Completamento – approfondimento di argomenti
parzialmente svolti nella prima
…
Geometria 1
Mod. M
Unità 2
Pgg 162 - 175
EQUAZIONI LINEARI LETTERALI
Equazioni lineari intere con un 1 parametro solo nei
coefficienti, con solo il parametro a denominatore, fratte
senza il parametro a denominatore, fratte con anche il
parametro a denominatore: discussione (1 solo
parametro) e scrittura del risultato in forma tabulare (?)
Algebra 1
Mod. D
Unità 1
Pgg 360 – 363
INTRODUZIONE AL PIANO CARTESIANO e
FUNZIONI NUMERICHE
Piano cartesiano per rappresentare funzioni numeriche
Proporzionalità diretta
Proporzionalità inversa
Proporzionalità affine (𝑓(𝑥) = 𝑎𝑥 + 𝑏)
Proporzionalità quadratica (cenni alla parabola)
Def. di valore assoluto e funzione valore assoluto
I vettori come coppia di punti sul piano cartesiano
[Excel potrebbe aiutare?]
Algebra 1
Mod. A
Unità 3
Pgg 118 – 121
Algebra 2
Mod. G
Unità 3
Pgg 357 – 363
Ottobre
(verifica)
SISTEMI LINEARI e PROBLEMI
Metodi risolutivi dei sistemi lineari numerici a due eq.
in due incognite, tre eq. in tre inc. e più
Problemi con più di una incognita
Modellizzazione
e
rappresentazione
grafica
(intersezione di rette, soluzione di equazioni, …)
Discussione di sistemi lineari a due eq. in due inc. con 1
parametro
Algebra 1
Mod. D
Unità 3
Pgg 432 – 497
Ottobre Novembre
(verifica)
GEOMETRIA
La circonferenza
I poligoni inscritti e circoscritti
Geometria 1
Mod. M
Unità 3 e 4
Pgg 176 - 227
Novembre –
Dicembre
(verifica per
Natale)
Settembre
(verifica)
SECONDA
Temi - argomenti
Sul testo
tempi
LE DISEQUAZIONI
Disequazioni lineari
Disequazioni scomponibili in fattori e disequazioni
fratte
Sistemi di disequazioni
Equazioni e disequazioni con valori assoluti (al
massimo 2)
Algebra 1
Mod. D
Unità 4 e 5
Pgg 498 – 561
Gennaio
(verifica)
I NUMERI REALI ed i RADICALI
Oltre ℚ: gli irrazionali
Notazioni ed approssimazioni
Irrazionalità di √2
Radice come operazione inversa della potenza
Radice come funzione (quindi dominio/C.E.)
Radice come espressione dell’esponente frazionario
Calcolo con i radicali
Razionalizzazione (1 rad. quadrata a denom. come
fattore, max. 2 radici quadrate a denom. come addendi,
una radice qualsiasi a denom. come fattore)
Semplici equazioni a coefficienti irrazionali
IL SECONDO GRADO
Equazioni
Disequazioni
Problemi
Discussione di equazioni letterali con 1 parametro
Equazioni parametriche
Algebra 2
Mod. E
Unità 1 e 2
Pgg 2 – 108
Geometria 2
Mod. N
Unità 1
Pgg 5 – 6
Algebra 2
Mod. F
Unità 1
Pgg 124 – 199
Febbraio
(verifica)
Marzo
(verifica)
Geometria 1
Mod. M
Unità 5
Pgg 228 – 255
GEOMETRIA
Equiscomponibilità ed equivalenza di figure piane
Il teorema di Pitagora
I due teoremi di Euclide
Problemi algebrici di applicazione dei tre teoremi sui
triangoli rettangoli
Algebra 1
Mod. D
Unità 2
Pgg 412 – 413
Geometria 2
Mod. N
Unità 4
Pgg 74 – 75
Aprile
(verifica)
SECONDA
Temi - argomenti
Sul testo
tempi
PROBABILITÀ e STATISTICA (*)
Definizione classica di probabilità, suoi limiti e cenni
alle definizioni alternative
Statistica descrittiva:
 Medie
 Moda
 Mediana
 Indici di variabilità dei dati
 Costruzione, lettura ed interpretazione di grafici
 Raccolta dati
Sul web
Mod. I
Unità 2, 3 e 4
Pgg 28 - 148
Prima parte di
Maggio
(verifica)
GEOMETRIA
Le trasformazioni geometriche:
 Isometrie
 Omotetie
 Similitudini con cenni ai criteri di similitudine dei
triangoli
Geometria 2
Mod. O
Unità 1
Pgg 102 – 171
Geometria 2
Mod. N
Unità 3
Pgg 35 – 69
Ultima parte di
Maggio
(verifica?)
(*) La presenza di questo argomento è determinata dal fatto che risulta presente nelle prove
INVALSI quindi potrebbe essere utile trattarlo. Però è vero anche che tale argomento viene ripreso
ed ampliato in terza, dove compare sul libro di testo (vol. 3). Si potrebbe allora saltarlo per avere
più possibilità di completare il resto del programma.
Alcuni argomenti non sono espressamente trattati nel testo (per fare un esempio, le omotetie e le
similitudini come trasformazioni) ma vi si trovano accenni in parti variamente distribuite. Inoltre,
sono segnati capitoli con ben più materiale di quanto nelle intenzioni sia richiesto (per fare un
esempio il calcolo combinatorio): regolarsi come meglio si ritiene.
Effettivamente il volume Geometria 2 risulta sottoutilizzato anche se, parecchio materiale, potrebbe
tornare utile nel proseguo della carriera scolastica.