Probabilità 2`016

Elementi di calcolo della probabilità
I concetti primitivi della teoria della probabilità sono:
- la prova;
- l’evento;
- la probabilità.
Si può dire che:
la prova genera l’evento con una certa probabilità.
La prova è un esperimento che ha due o più possibili risultati e in relazione al risultato che si
presenterà si avrà un certo grado di incertezza.Le diverse fasi in cui può essere suddivisa una
prova si definiscono sottoprove.
L’evento è uno dei possibili risultati di una prova.
La probabilità è un numero compreso tra 0 e 1 e misura il grado di incertezza del verificarsi di
un evento.
Definizione classica della probabilità:
La probabilità è data dal rapporto tra il numero dei casi favorevoli all’evento e il numero dei
casi possibili purchè tutti ugualmente possibili.
n.dicasifavorevoli
P E  
n.dicasiposs ibili
Le diverse concezioni della probabilità
Accanto al concetto classico si hanno diversi concetti di probabilità:
concezione frequentista legata alla ripetibilità della prova.Gli esiti della prova che di volta in
volta si presenteranno, non necessariamente saranno sempre uguali e allora potremo osservare la
frequenza con cui si presentano i singoli eventi elementari e dire che :
P E  
ni
n
si fa così ricorso all’analogia tra probabilità e frequenza relativa riferita a n prove ripetute sotto
le stesse condizioni.
A questo proposito occorre ricordare il postulato empirico del caso:
se si effettuano n prove sotto le stesse condizioni ciascuno degli eventi possibili compare
con una frequenza che si approssima alla sua probabilità. Questa approssimazione diventa
sempre più elevata al crescere n del numero delle prove.
Concezione soggettiva
In questa concezione la probabilità viene intesa coma la misura del grado di fiducia che un
individuo ha riguardo al possibile verificarsi di un certo evento
Due concetti sono molto importanti ai fini dello studio degli eventi e della loro probabilità: la
somma logica e il prodotto logico.
Per somma logica o unione si intende fare riferimento a tutti gli elementi che sono comuni ad A
e B: Tale somma si indica con :
A  B e si legge ‘A unione B’ o ‘A o b’ dove ’ o’ ha il significato di A, o B o entrambi.
Il prodotto logico o intersezione di due insiemi si indica con :
1
A  B e si legge A e B o A intersezione B cioè comprende l’insieme dei punti che sono comuni
ai due eventi. Nel linguaggio degli insiemi l’appartenenza a due insiemi diversi viene
sintetizzata dalla parola ‘e’.
Al simbolo di appartenenza A  B cioè A è una parte di B si collega il concetto di
implicazione per gli eventi. Si dirà infatti che l’evento A implica l’evento B quando si vuole
significare che l’evento A non può verificarsi se non si verifica anche l’evento B.
Due insiemi sono disgiunti quando non hanno alcun punto in comune, cioè non è possibile
calcolare la loro intersezione. Si dirà anche che i due eventi sono incompatibili.
Due eventi sono esaustivi quando non è possibile che non se ne verifichi nessuno e cioè l’uno,
l’altro o entrambi devono verificarsi.
Uno spazio campionario formato da un numero finito di eventi prende il nome di spazio
campionario discreto.
Probabilità condizionata
Se siamo interessati a conoscere la probabilità di un evento dato che si è in presenza di un
evento condizionante parliamo di probabilità condizionata. La simbologia usata per indicare tale
probabilità considerato per esempio due eventi A e B è P A / B che si legge probabilità di A
dato B.
La probabilità di A dato B è uguale alla probabilità intersezione tra i due eventi diviso la
probabilità dell’evento che condiziona l’esperimento :
P A  B 
con P (B )  0
P B 
da questa relazione segue che :
P A / B  
P A  B  P A / BPB  PB / AP A
Se P A / B  P A l’aver saputo che si è verificato l’evento B ha modificato la probabilità
dell’evento A e si dice che i due eventi sono dipendenti:
Se P A / B  P A invece il verificarsi dell’evento B non ha alcuna influenza sulla probabilità
dell’evento A e i due eventi sono indipendenti.In questo caso la probabilità intersezione sarà
uguale a :
P A  B  P A  PB
N.B. Se l’evento A è indipendente da B anche B è indipendente da A.
In conclusione consideriamo il seguente schema riferito a due eventi A e B :
eventi A e B
A e B si escludono a vicenda
P A  B  P A  PB
P A  B  Ǿ
A e B non si escludono a vicenda
P A  B  P A  PB  P A  B
P A  B
dipendenti
P A  B  P APB / A
indipendenti
P A  B  P APB
2
Esercizio
Un esperimento ha condotto ai seguenti risultati:
1
1
1
P  A  ; P B   ; P  A  B  
3
2
4
si chiede di calcolare:


 
  
  

P A  B ; P A  B ; P A  B ; P B  A ; P A / B ; PB / A

 
 

Risoluzione
In base ai dati a disposizione si consiglia, come prima operazione, di compilare una tabella 2 per
2 nel modo che segue:
B
A

B
1
4
1
3
1
2
1

A
Troviamo ora in base ai dati su esposti le probabilità incognite. Si avrà :


 1 1 43 1
P A  B    

12
12

 3 4
e ragionando allo stesso modo:
 
 1 1 2 1 1
P A  B    

4
4

 2 4
e ancora:

 
 1 1 6 1 5
P A  B   


12
12

 2 12
3
La tabella definitiva assumerà la seguente forma:
B
A
1
4

1
A
4
Totale 1
2

B
totale
1 1
12 3
5 2
12 3
1 1
2
Ora calcoliamo le probabilità richieste:
P  A  B   P  A  P  B   P  A  B  
1 1 1 463 7
  

3 2 4
12
12

 
 5
P A  B  

 12


 

  
  
 
 2 1 5 865 9
P A  B   P A   P B   P A  B    


12
12


 
 

 3 2 12
 
 1
P B  A  

 12
1
P A  B  4 1 2 1
P A / B  
   
1 4 1 2
P B 
2
La probabilità ottenuta è diversa dalla probabilità di A quindi i due eventi sono dipendenti.
1
P B  A 4 1 3 3
P B / A 
   
1 4 1 4
P  A
3
Come si può notare le due probabilità condizionate hanno lo stesso numeratore , possiamo
perciò scrivere che:
P  A / B   P  B   P  B / A  P  A 
1 1 3 1 1
   
2 2 4 3 4
4
e da questa relazione si ottiene che:
P  B / A 
P  A / B   P B 
P  A
che prende il nome di teorema di Bayes dal nome dello studioso che per primo si è interessato
del problema e l’importanza di questo teorema è che può essere generalizzato a più eventi e
verrà esaminato in maniera più approfondita più avanti.
Esercizio
Tra i 250 studenti che frequentano le lezioni di statistica 170 hanno superato l’esame di
matematica. Tra gli studenti che hanno superato l’esame 90 sono donne mentre sono 50 i maschi
che non lo hanno superrato.Dopo aver costruito la tabella con i dati rilevati si chiede di costruire
la corrispondente tabella di probabilità.
Risoluzione
La tabella ottenuta è la seguente:
S

S
M
80
50
F
90
30
totale
170
80
totale 130 120 250
E la corrispondente tabella di probabilità si otterrà dividendo ciascuna frequenza assoluta per il
totale delle osservazioni, ottenendo:
esito/ sesso M
F totale
S 0.32 0.36 0.68

0.2 0.12 0.32
S
totale 0.52 0.48
1
Ora calcoliamo le seguenti probabilità:
PS  D  PS   PD  PS  D  0.68  0.48  0.36  0.8
PS  M   PS   PM   PS  M   0.68  0.52  0.32  0.88
PS / F  
PS  F  0.36

 0.75
P F 
0.48
PS / M  
PS  M  0.32

 0.62
PM 
0.52
5
Esercizio
Una commissione è formata da 10 professori di Statistica e 8 professori di matematica. In
ognuno dei due gruppi 5 professori sono donne. Se si sceglie come relatore una donna qual è la
probabilità che sia professore in Statistica?
Risoluzione
Per prima cosa costruiamo la tabella relativa ai dati a disposizione:
Materie\Sesso Uomini Donne totale
Prof. Stat.
5
5
10
Prof. Matem.
3
5
8
totale
8
10
18
Posso calcolare la probabilità di estrazione di una donna che è pari a :
P D  
10
18
mentre la probabilità che la donna sia professore in statistica è pari a :
PD  P.S . 
5
18
allora la probabilità richiesta sarà uguale a :
5
5 1
PP.S . / D   18 

10 10 2
18
6
Esercizio
Costruire lo spazio campionario relativo al lancio di 4 monete.
Risoluzione
Ogni moneta ha due casi possibili testa o croce e in quattro lanci i casi possibili saranno 24=16,
quindi lo spazio campionario sarà composto da 16 eventi ognuno con probabilità pari a 1/16. Lo
spazio campionario , risultato dell’esperimento, è il seguente:
TTTT
TTTC
TTCT
TTCC
TCTT
TCTC
TCCT
TCCC
CTTT
CTTC
CTCT
CTCC
CCTT
CCTC
CCCT
CCCC
Partendo dallo spazio campionario ottenuto si chiede di:
-costruire la tabella a doppia entrata in cui la v.c. X rappresenta dal numero delle teste uscite,
mentre la variabile Y si riferisce al numero delle variazioni nella sequenza dei lanci;
- calcolare la media e la varianza delle due variabili;
- calcolare la covarianza;
- costruire la distribuzione somma e di calcolare la media e la varianza dimostrando le
relazioni studiate.
Costruiamo la tabella richiesta in cui per quanto riguarda la variabile X i casi di uscita di
numero di teste in quattro lanci sono rappresentate dai valori: 0,1,2,3,4,mentre con riferimento
alle variazioni che si possono verificare nella sequenza dei lanci si avranno i valori : 0 quando si
presenta sempre la stessa faccia, 1 se all’uscita di una testa o di una croce seguono o tutte croci
o tutte testa, 2 o 3 se si verificano due o tre variazioni nella sequenza dei lanci . La tabella che si
ottiene è la seguente:
x\y
0
1
2
3
0 1/16
/
/
/
1
/ 2/16 2/16
/
2
/ 2/16 2/16 2/16
3
/ 2/16 2/16
/
4 1/16
/
/
/
totale 2/16 6/16 6/16 2/16
totale
1/16
4/16
6/16
4/ 16
1/16
16/16=1
7
Calcoliamo la media aritmetica e la varianza delle due distribuzioni :
 x   x i p  xi  
i
1 4  2  6  3  4  4  1 32

2
16
16
 x2   xi2 pxi    x2 
i
 y   y j py j  
j
1 4  4  6  9  4  16  1 2 80
2 
 4  5 4 1
16
16
1  6  2  6  3  2 24

 1.5
16
16
 y2   y 2j p y j    y2 
j
1 6  4  6  9  2
48
 1.5 2 
 2.25  3  2.25  0.75
16
16
Per il calcolo della covarianza costruiamo la tabella che ci fornisce la sommatoria del prodotto
delle due variabili ponderate con le corrispondenti probabilità: Il prospetto che si ottiene è il
seguente:
x\y
0
0
/
1
/
2
/
3
/
4
/
totale 2/16
1
2
3
totale
/
/
/
/
2/16 4/16
/ 6/16
4/16 8/16 12/16 24/16
6/16 12/16
/ 18/ 16
/
/
/
/
6/16 6/16 2/16 48/16
cov xy    xi y j p xi y j    x   y 
48
 2  1.5  3  3  0
16
i
j
La covarianza è uguale a zero ma noi sappiamo che sicuramente tra le due variabili casuali c’è
una qualche relazione perché nella tabella che abbiamo costruito abbiamo diverse caselle vuote
quindi concludiamo dicendo che non è presente relazione di tipo lineare.
Distribuzione somma
La distribuzione che si ottiene sommando le due variabili è la seguente:
si
0
2
3
4
5
totale
p(si)
1/16
2/16
4/16
5/16
4/16
16/16=1
8
Nel prospetto che segue figurano i calcoli per la media e la varianza della distribuzione somma:
si
p(si)
1/16
2/16
4/16
5/16
4/16
16/16=1
0
2
3
4
5
totale
sip(si) si2 si2p(si)
/ /
/
4/16 4
8/16
12/16 9 36/16
20/16 16 80/16
20/16 25 100/16
56/16
224/16
 s   si psi  
i
56
 3.5
16
 s   x   y  2  1.5  3.5 c.v.d.
La media della distribuzione somma è anche uguale alla media della distribuzione x più la
media della distribuzione y.
 s2   si2 psi    s2 
i
224
 3.5 2  14  12.25  1.75
16
 s2   x2   y2  1  0.75  1.75 c.v.d.
La varianza della somma, nel caso che stiamo esaminando, è uguale alla varianza della
distribuzione x aumentata della varianza della distribuzione y. Infatti abbiamo osservato che tra
le due variabili non esiste relazione di tipo lineare e quindi il doppio della covarianza è uguale a
zero.
La distribuzione riferita alle diverse somme campionarie con le corrispondenti probabilità è
chiamata distribuzione stimatore e le singole si sono le stime della somma calcolate campione
pert campione
9
TEOREMA DI BAYES
Il teorema di Bayes è un’applicazione della probabilità condizionata che risulta molto
importante per gli sviluppi e l’interpretazione che consente di avere in termini di probabilità.
La probabilità intersezione abbiamo visto essere uguale a un prodotto:
PE  A  PE / AP A e ancora dal momento che :
PE  A  P A / E PE  possiamo scrivere che :
P A / E PE   PE / AP A che porta al seguente risultato :
P  E / A 
P A / E PE 
P  A
noto in letteratura come teorema di Bayes.
La probabilità condizionata PE / A può essere ottenuta sia attraverso l’applicazione della
formula della probabilità condizionata sia mediante il teorema di Bayes che a prima vista può
apparire più complicato ma che fornisce una interpretazione molto più dettagliata del risultato
ottenuto perché fa vedere come PE / A sia proporzionale al prodotto della probabilità
marginale PE  per la condizionale inversa P A / E  .
Questa interpretazione della probabilità condizionata può essere generalizzata a i eventi . Infatti
se gli eventi 1, 2, …n formano un sistema completo di eventi cioè una partizione finita la
probabilità di un qualunque evento A  I può essere definita facendo riferimento alle probabilità
dei singoli eventi Ei . Possiamo cioè scrivere :
N
P A   PEi P A / Ei 
i 1
Infatti se gli eventi formano una partizione si ha che :
N
P A   P A  Ei   P A / Ei PEi 
i 1
Tale risultato può essere illustrato attraverso questo diagramma:
E1
E2
………….
………………..
A
………………..
EN
10
che mostra una partizione completa e l’evento sovrapposto A .
L’interpretazione più immediata che risulta da questo diagramma è che gli eventi Ei possono
considerarsi come le cause che determinano A. Questo fa sorgere il problema di trovare una
relazione che permetta di calcolare la probabilità che sia stato Ei a determinare A dato che l’evento
A si è verificato.
Ritornando alla formula della probabilità condizionata abbiamo visto che :
P  E i / A 
P  E i  A
P  A
e ancora :
PEi  A  PEi P A / Ei  e possiamo quindi scrivere la formula di Bayes generalizzata a N
eventi tra loro incompatibili :
P E i / A 
P A / Ei PEi 
N
 P A / E PE 
i 1
i
i
Le probabilità degli eventi Ei che sono le cause che possono generare l’evento A sono chiamate
probabilità a priori , sono probabilità soggettive e non dipendono dall’esperimento ; le probabilità
condizionate P A / Ei  vengono definite probabilità probative o verosimiglianze e rappresentano le
probabilità con cui le singole cause Ei generano l’evento A. Esse sono determinate empiricamente
dall’esperimento. Le probabilità PEi / A sono le probabilità a posteriori delle cause Ei, sapendo
che l’evento A si è verificato indicano con quale probabilità Ei ha agito nel determinare A.Il
teorema di Bayes viene interpretato come un meccanismo che permette di correggere le
informazioni a priori sulla base delle informazioni sperimentali consentendo in tal modo di arrivare
alle probabilità a posteriori. Compaiono infatti in questa formula informazioni a priori non
verificate empiricamente e verosimiglianze risultato di un esperimento e quanto più la probabilità a
posteriori PEi / A sono diverse dalle probabilità a priori tanto più si dirà che le verosimiglianze
hanno modificato le informazioni a priori sulle cause Ei.
Esercizio
Nella sessione di luglio l’esame di Statistica è stato superato dal 40% degli studenti donne e dal
30% degli studenti uomini: Le donne rappresentano il 52% degli studenti.
Uno studente scelto a caso ha superato l’esame di Statistica, qual è la probabilità che sia una donna?
Risoluzione
Siamo in presenza di un problema la cui soluzione va ricercata applicando il teorema di Bayes: I
dati a nostra disposizione sono i seguenti:
PD   0.52
PU   0.48
PS / D   0.40
PS / U   0.30
11
Ora dal momento che lo studente estratto ha superato l’esame di Statistica si vuole sapere se si è
modificata la probabilità a priori relativa al fatto che lo studente sia uomo o donna: La probabilità
ricercata è pertanto una probabilità a posteriori e sarà data da:
P D / S  
PS / D   PD 
0.40  0.52
0.208
0.208



 0.59
PS / D   PD   PS / U   PU  0.40  0.52  0.30  0.48 0.208  0.144 0.352
Si è presentato l’evento ‘superato l’esame di statistica’ e la probabilità a priori è stata modificata da
0.52 è passata a 0.59. Lo stesso ragionamento lo possiamo fare con riferimento agli studenti uomini
e la probabilità a posteriori assumerà il valore:
PU / S  
PS / U   PU 
0.30  0.48
0.144
0.144



 0.41
PS / U   PU   PS / D   PD  0.30  0.48  0.40  0.52 0.144  0.208 0.352
Le probabilità a priori si sono così modificate:
sesso
p. a priori
p. a posteriori
Uomini
0.48
0.41
Donne
0.52
0.59
totale
1
1
Dal prospetto si vede immediatamente che dal momento che la maggior probabilità di superare
l’esame si aveva in corrispondenza degli studenti donne il fatto di sapere che lo studente estratto ha
superato l’esame modifica la probabilità di avere uno studente che ha superato l’esame di sesso
femminile facendo sì che la probabilità a posteriori sia più elevata mentre diminuisce la stessa
probabilità riferita agli studenti di sesso maschile.
12
Variabili casuali
Una variabile casuale solitamente indicata con v.c. è l’insieme di tutte le possibili determinazioni
della variabile casuale X : x1, x2,…xn ed è sempre accompagnata dalla corrispondente probabilità.
La v.c. è il risultato di un esperimento e a questo risultato si fa corrispondere un numero reale.Le
variabili casuali possono essere discrete o continue.
Variabili casuali continue
La curva normale
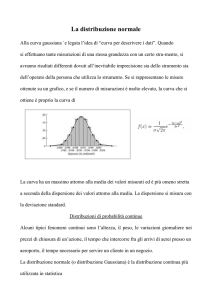
I fenomeni che, rappresentati graficamente, danno origine ad una curva normale sono molto
numerosi e si tratta di fenomeni quali il reddito, la statura, etc. Questi fenomeni infatti si presentano
con la stessa forma degli errori accidentali che rappresentati graficamente danno origine alla curva
normale o di Gauss.
La funzione di densità di una distribuzione normale può essere considerata o nella forma
completa oppure nella forma standardizzata che di seguito esamineremo.
LA DISTRIBUZIONE NORMALE COMPLETA
La funzione di densità di una curva normale è la seguente :
y= f  x  
1
2
2
e
1
 
2

xi  M 1 

2


quando le frequenze sono relative e quindi la loro somma è uguale all’unità.Se invece le frequenze
che
vengono
y  f x  
prese
N
2 2
e
in
1  x  M1 
 

2  
considerazione
sono
quelle
assolute
l’ordinata
sarà
:
2
Tale funzione è sempre positiva (per  > 0) e Quando una variabile ha una tale funzione di
densità si dice che è distribuita in modo normale.
Questa distribuzione dipende da due parametri M1 e , mentre π è il rapporto tra la
circonferenza e il diametro del cerchio ed “e” è la base dei logaritmi neperiani,2,71828.
1
è un fattore di scala che fa sì che l’area sottesa dalla curva sia pari all’unità mentre la parte
2
esponenziale,legata ad e ,è responsabile della forma campanulare e della simmetria della curva.
13
La curva presenta le seguenti caratteristiche:
1. è asintotica rispetto all’asse delle ascisse ;
2. è crescente nell’intervallo (- , M1) e decrescente nell’intervallo (M1, + )
3. media, moda e mediana sono coincidenti;.
4.
ha l’indice di asimmetria pari a zero e quindi la curva è simmetrica rispetto alla retta che
passa per il punto x= M1.Si ha cioè f(-x +M1) = f( x + M1 ) e, in relazione a questa proprietà, gli
errori negativi e positivi , uguali in valore assoluto, hanno la stessa probabilità di verificarsi.
5. ha curtosi pari a 3 dove per curtosi si intende il grado di appiattimento che una curva presenta
rispetto all’asse delle ascisse. Tale valore di curtosi è una caratteristica propria della normale.
Nel punto di massimo si ha che x= M1 e la funzione assume il valore:
f M1  
1
1
  0,3989
2  
e quindi l’altezza massima della curva è inversamente proporzionale al
.
Al variare di M1 con  costante, la forma delle curva rimane inalterata ed ha luogo solo una
traslazione della stessa sull’asse delle ascisse.
1 = 2 = 3
M 1 < M2 < M3
-
M1
M2
M3
+
Al variare di  invece la sua forma varia assumendo una forma allungata per bassi valori di  e
schiacciata per alti valori di .
Se la situazione che si presenta è:
 
1
2
 3
con M1 costante nelle tre distribuzioni, i grafici saranno relativi alle tre
curve saranno:
14
σ3
σ2
σ1
 = =
1 2 3
-
+
La curva presenta due punti di flesso in corrispondenza di M1+  e M1 -  .
L’area sottesa dalla curva vale 1, l’asse di simmetria la divide in due parti simmetriche di area 0,50.
LA CURVA NORMALE STANDARDIZZATA
La risoluzione dei problemi legati alla curva normale richiede la conoscenza delle frequenze
relative che cadono all’interno di un certo intervallo, e questa ottenuta per via analitica
comporterebbe dei calcoli troppo complicati e laboriosi. Infatti per calcolare la frequenza relativa
dei casi compresi nell’intervallo a, b si dovrebbe calcolare l’integrale :
 f xdx  
b
b
a
a
1
2 2
e
1  x  M1 
 

2  
2
dx
Per questo motivo si è costruito un modello tipico (o standard) di curva normale che fa ricorso
alla trasformazione della variabile x in z.
Ricordando che :
z
x  M1

la funzione di densità della curva normale si trasforma in:
f z  
1
 1 
exp  z 2 
2
 2 
che presenta media uguale a 0 e varianza pari a 1.
15
Questa curva presenta le seguenti caratteristiche:
1) ha il punto di massima ordinata in corrispondenza del valore 0, media della variabile
standardizzata z;
2) il valore massimo dell’ordinata della curva vale 0,3989;
3) presenta due punti di flesso in corrispondenza del valore  1.
Di questa curva sono stati tabulati i valori delle aree e delle ordinate e questo evita perciò di
volta in volta il calcolo degli integrali. Queste due tavole possono poi con opportuni adattamenti
riferirsi anche alla curva normale completa.
La tavola delle ordinate è quella sicuramente meno usata e fornisce in corrispondenza dei valori
di z le densità di frequenza corrispondenti. Anche in questo caso è opportuno notare che mentre il
campo di variazione dell’asse delle ascisse va da -
 +  i valori di z vanno da 0 a 3.99 perché
quando z è molto grande il valore dell’ordinata è vicinissimo allo zero.
La tavola delle aree è di gran lunga la più importante e fornisce il valore dell'area sottesa dalla
curva in corrispondenza di un determinato intervallo. Diverse sono le tipologie di tavole che
possono essere prese in considerazione e sono corrispondenti alle seguenti situazioni:
a) tavole che forniscono l’area relativa a un intervallo simmetrico  z :
b) tavole che forniscono l’area compresa tra l’asse di simmetria e l’ordinata corrispondente a
+z ;
c) tavole che forniscono l’area compresa tra -
 e l’ordinata corrispondente a +z..
Le tavole che solitamente verranno usate per la risoluzione degli esercizi sono quelle del tipo b)
nelle quali i valori di z figurano nelle colonna esterna mentre i valori delle aree relative
all’intervallo richiesto figurano all’interno della stessa .I valori tabulati all’interno
corrispondono all’integrale:
Area =
 z2 
exp  dz
2
 2
z1 1

0
I problemi che si possono presentare sono:
-
di tipo diretto se ,dati due valori di z ,vogliamo conoscere il valore della frequenza
corrispondente all’intervallo considerato;
-
di tipo inverso se , nota una certa frequenza, vogliamo risalire all’intervallo corrispondente.
L’utilizzo delle tavole, nelle quali in corrispondenza dei valori da zero a z troviamo il valore
dell’integrale, e le caratteristiche della curva permettono di risolvere ogni problema relativo alla
curva normale. Infatti, se un fenomeno ha una distribuzione f(x) normale, la probabilità (frequenza
16
relativa) che una osservazione abbia un valore compreso tra x 1 e x2 è pari all’area sottesa dalla
x  M1
x  M1
curva normale standardizzata tra i punti z1  1
e z2  2
equivalente all’integrale:


z2 1
 z2 
exp
 2   2 dz
z1
I valori di z tabulati vanno da 0 a 3,99 e, in corrispondenza di questo valore la frequenza dei casi
per una metà della curva è uguale a 0,49997. Questo significa che in un intervallo  3,99 è
compreso lo 0,9999 dei casi, cioè la quasi totalità.
Particolare interesse rivestono alcuni intervalli simmetrici intorno alla media e le ampiezze degli
area =
intervalli simmetrici in cui si comprendono talune particolari frequenze:
Fr (   0.5  x    0.5 )  Fr (0.5  z  0.5)  0.3829  38.3%
Fr (     x     )  Fr (1  z  1)  0.6826..  68.3%
Fr (   1.5  x    1.5 )  Fr (1.5  z  1.5)  0.86638  86.6%
Fr (   2  x    2 )  Fr (2  z  2)  0.95450  95.4%
Fr (   2.5  x    2.5 )  Fr (2.5  z  2.5)  0.98758  98.8%
Fr (   3  x    3 )  Fr (3  z  3)  0.99730  99.7%
Gli intervalli considerati sono stati esaminati con riferimento alla variabile x osservata e alla
variabile z standardizzata e sono chiamati anche limiti tipici di scarto .E’ immediato notare che,
come abbiamo precedentemente affermato, la quasi totalità dei casi cade nell’intervallo simmetrico
 3 o  3 .
Intervalli simmetrici relativi a particolari frequenze:
0.50  Fr (0.67  z  0.67)  Fr (   0.67  x    0.67 )
0.80= Fr (1.28  z  1.28)  Fr (   1.28  x    1.28)
0.90= Fr (1.64  x  1.64)  Fr (   1.64  x    1.64)
0.95= Fr (1.96  z  1.96)  Fr (   1.96  x    1.96 )
0.99= Fr (2.58  z  2.58)  Fr (   2.58  x    2.58)
ESERCIZIO
Trovare il valore di k in modo che la funzione:
f ( x) 
k
x 1
con (x= 2,4,5,6 ) sia una distribuzione di frequenze relative.
Se la distribuzione è di frequenze relative possiamo scrivere :
k

i 1
 k 
f x    

i 1  x  1 
k
17
k
 1 
1  k 

i 1  x  1 
dal momento che la somma delle frequenze relative è pari all’unità. Sostituendo i valori dati si avrà:
1
1
1 
 1
1  k




1 1 2 1 3 1 4 1
1 1 1 1
1  k    
 2 3 4 5
77
 30  20  15  12 
1  k
k
60
60


k=
60
77
ESERCIZIO
Sapendo che la statura di una popolazione di N = 5.000 unità si distribuisce secondo una normale
con media pari a 174 e  = 9, determinare:
1. la percentuale e il numero dei soggetti con statura compresa tra 165 e 172 cm;
2. il numero dei soggetti compreso tra 168 e 180 cm;
3. il numero dei soggetti con statura inferiore a 160 cm;
4. il numero delle unità con statura maggiore a 178 cm;
5. qual’è la statura massima del 5% dei soggetti più bassi ?
6. qual’è la statura minima del 3% dei soggetti più alti ?
Risoluzione
1) Il primo passo da fare per la risoluzione degli esercizi quando non abbiamo il valore di z, da
cercare sulle tavole, è quello di standardizzare i valori. In questo caso si avrà:
z1 
165  174
 1
9
z2 
172  174
 0,22
9
18
Si disegna la curva normale e si individuano i due valori di z:
-
-1 -0,22
0
+
Poiché le tavole forniscono i valori tabulati dell’area tra 0 e z, in questo caso dovremo fare la
differenza tra due aree.
L’area tra z = 0 e z = - 1 e l’area tra z = 0 e z = - 0,22.
Sarà quindi:
Fr (-1 < z < - 0,22) =
0,34134 – 0,08706 = 0, 26428
La frazione dei casi compresa nell’intervallo è quindi di circa il 26,43% ed il numero delle unità
sarà pari a 1321; cioè :
5000  0,2643  1321
2) z1 
168  174
 0,67
9
z2 
180  174
 0,67
9
Questa volta l’intervallo è simmetrico rispetto al punto di massima ordinata con media pari a 0
e nel grafico sarà:
19
-
- 0,67
0
+ 0,67
+

Si tratterà quindi di effettuare la somma di due aree:
l’area compresa tra 0 e – 0,67 e l’area tra 0 e + 0,67.
Quindi:
Fr (- 0,67 < z < + 0,67) =2Fr ( 0  z  0,67) = 0,24857 . 2 = 0,49719  49,7
ed il numero delle unità sarà di: 2486
3) frequenza dei casi con statura inferiore a 160 cm;
Fr = (z < 160) = Fr (z < (160 – 174) / 9 ) =
Fr = (z < - 14 / 9 ) = Fr (z < - 1,56) = 0,5 – Fr ( 0  z  1,56 ) = 0,5 – 0,44062  0,06
-
- 1,56
0
+

L’area si trova per differenza tra l’area compresa tra 0 e –  pari a 0,50 e,l’area tra 0 e 1,56:
Il numero dei soggetti sarà:
0,05938 . 5000 = 297
4) Fr ( X > 178) =
Fr ( Z > (178 – 174) / 9) =
= Fr (z > 0,44) = 0,5 –Fr ( 0  z  0,44)  0,5 – 0,17003= 0,32997
 33%
0,32997 . 5000 = 1650 soggetti
20
-
0
0,44
+
5) Individuiamo il 5% dei casi nella parte sinistra della curva normale perché stiamo parlando
di basse stature:
5%
-
-z
0
+
L’area da 0 a z vale 45% ovvero: 0,45 (0,50 – 0,05).
Leggendo sulle tavole ad un’area pari a 0,4495 corrisponde il valore z= 1,64, mentre l’area
0,4505 corrisponde a z=1,65. Per trovare il valore di z che corrisponde esattamente a un’area di
0,45 possiamo interpolare tra i due valori di z e le corrispondenti aree.
Abbiamo i seguenti valori:
z
area
1,64 0,4495
z
0,45
1,65 0,4505
Possiamo trovare il valore di z incognito con una interpolazione lineare ( assumiamo cioè che
nell’intervallo (1,64  z 1,65) la curva normale possa essere approssimata da una retta).
Si ha:
z  1,64
0,45  0,4495

1,65  1,64 0,4505  0,4495
e risolvendo rispetto a z :
21
z  (1,65  1,64) 
0,0005
 1,64  0,01  0,5  1,64  0,005  1,64  1,645
0,001
Ora dal valore standardizzato risaliamo al valore di x = statura ricordando che siamo nella parte
negativa
 1,645 
della
curva.
Scriveremo
perciò:
x  174
 1,645  9  174  x  14,805  174  159,195
9
Quindi la statura massima del 5% dei soggetti più bassi è di cm 159,195.
6) Lo stesso ragionamento adottato nel punto precedente si applica anche per risolvere questo
caso, con la differenza che questa volta siamo interessati alla coda destra, perchè parliamo di
alte stature.
3%
-
0
z
+
0,50 – 0,03 = 0,47
Per trovare il valore esatto di z dovrei interpolare tra i valori di z= 188 e z = 1,89 ma
ragionevolmente possiamo adottare z= 1,89 , quindi:
1,89 
x  174
 1,89  9  174  x  17,01  174  191,01
9
La statura massima del 3% dei soggetti più alti è pari a cm 191, 01.
Il teorema di Bienaymé – Tchebycheff
Quando la forma della distribuzione non è nota non è possibile l’utilizzo della normale e i problemi
relativi alla ricerca della frequenza relativa di un certo intervallo possono essere risolti solo con
l’ausilio della disuguaglianza di Tchebycheff che permette di trovare i limiti superiori e inferiori di
22
un certo intervallo conoscendo le costanti caratteristiche della distribuzione, media aritmetica e
deviazione standard.
Il modo più immediato per determinare i limiti dell’intervallo non conoscendo la forma della
distribuzione è il seguente:
-

M1-kσ
M1
M1+kσ
+

indichiamo con xj i valori della variabile che cadono esternamente all’intervallo di cui vogliamo
determinare i limiti, intervallo che verrà espresso sotto la forma:
M 1  k ; M 1  k con   0 e k > 1 , in simboli si avrà:
x j  M 1  k 
x j  M 1  k 
 x j  M 1   k
x j  M 1  k

x j  M 1   k
 fr X  M 1  k 

x j  M 1  k

1
k2
cioè la frazione dei casi che cadono esternamente all’intervallo considerato è inferiore al risultato
1
del rapporto 2 .
k
Uno dei modi per dimostrare quanto affermato è partire dalla varianza della distribuzione che sarà
sempre maggiore della sommatoria dei quadrati degli scarti che riguardano le code della
distribuzione.Si potrà perciò scrivere la seguente disuguaglianza:
 2   xi  M 1 2 f i   x j  M 1 2 f j   j k 2 2 f j  k 2 2  j f j
k
k
i 1
i j
 2  k 2 2  f j
ora ,dividendo i termini della disuguaglianza per k 2 2 , si
j
otterrà:
1
 fj
k 2 j
e quindi la somma delle frequenze della distribuzione che cadono nelle code
,ovvero esternamente all’intervallo considerato, è minore di
Infatti :  f j  fr X  M 1  k 
j
1
.
k2
1
k2
23
Se
f
j
rappresenta la frazione dei casi che cade nelle code , la frazione complementare cadrà
j
invece all’interno dell’intervallo considerato e dal momento che l’area sottesa dalla curva è uguale
all’unità potremo scrivere:
1- Fr  x  M 1  k   1 
Fr  x  M 1  k   1 
1
k2
o ancora :
1
k2
Se il valore di k=2 si può quindi stabilire che la frazione dei casi che cadono esternamente
1
all’intervallo è minore di
 0.25  25% mentre la restante parte 75% cadrà all’interno
4
dell’intervallo M 1  2 , M  2 .
1
 0.11  11% è la frazione dei casi esterna all’intervallo mentre
9
l’89% è la frazione compresa nell’intervallo M1  3 , M1  3  .
Se nell’espressione del teorema eliminiamo il simbolo di valore assoluto si potrà scrivere che :
Per k=3 il teorema stabilisce che
Fr  k  x  M 1  k   1 
1
k2
Fr M 1  k  x  M 1  k   1 
1
k2
e quindi il teorema stabilisce che la frazione dei casi che in una distribuzione con media e varianza
1
finite cadono all’interno di un certo intervallo con k >1 è superiore a 1  2 .
k
Gli intervalli che abbiamo or ora definito sono una funzione crescente di  dal momento che in
corrispondenza del suo aumentare si avranno intervalli via via crescenti. Se invece il valore di  è
piccolo gli intervalli saranno concentrati intorno al valore della media che risulta così essere
veramente rappresentativa della distribuzione.
Distribuzione uniforme
Si è in presenza di una distribuzione uniforme discreta quando la variabile xi assume i valori: 1,2, N
1
ciascuno accompagnato da una frequenza una frequenza costante pari a :
la cui somma è
N
naturalmente pari all’unità.
Il diagramma a ordinate corrispondente a una distribuzione di questo tipo assumerà la forma:
fi
24
0
1
2
3
4
5
xi
in cui tutte le ordinate presentano la stessa altezza legata al fatto che nella distribuzione non esiste
moda.
Calcoliamo la media e la varianza di questa distribuzione:
Media aritmetica
1
1
1
1
 2   3   .....  N 
N
N
N
N  1 1  2  3  ...  N 
M1 
1
N
Ricordando che:
1
1  2  3  ..  N 
M1 
1 N
N si avrà:
2
1 1 N
1 N

N
N
2
2
Varianza
Calcoliamo la varianza con la formula:
 2  M 22  M 12
M 22 
12 
1
1
1
1
 2 2   3 2   .....  N 2 
N
N
N
N  1 12  2 2  3 2  ...  N 2
1
N


La somma :
12  2 2  3 2  ...  N 2  N
M 22 
12 
N  12 N  1
6
e sostituendo questo valore nella formula si ha che:
1
1
1
1
 2 2   3 2   .....  N 2 
N
N
N
N  1  N   N  12 N  1  N  12 N  1
1
N
6
6
25
Ora calcoliamo la varianza:

2
2

N  12 N  1  1  N 




6
 
2 
dopo aver svolto i prodotti,effettuato il quadrato del binomio, ricondotto la differenza allo stesso
denominatore ed effettuato tutte le possibili semplificazioni , si avrà:

2 N 2  N  2 N  1  1  N 2  2 N  4 N 2  2 N  4 N  2  3  3N 2  6 N N 2  1
 
 

6
4
12
12


La distribuzione rettangolare
La distribuzione rettangolare è l’equivalente della distribuzione uniforme nel continuo ed è
caratterizzata dal fatto di avere la funzione di densità sempre costante e pari a :
f x  
1
 
con  x
Il grafico corrispondente sarà:
f(x)
0


x
Calcoliamo la media e la varianza.
26
Media
Dal momento che siamo in presenza di una distribuzione continua dobbiamo far ricorso al calcolo
del seguente integrale:

M x    x 

1
1
dx 
 
 

1
1 2
1
1
 
1 2 
2



x















 2 
  2
2  
2



Varianza
Calcoliamo il quadrato della media quadratica:

M 22   x 2 



1
1
1
1
1
1
1 
dx 
  x 3    3   3 
  2     2    

 
   3  3
  3
 
 2     2
3
Ora possiamo applicare la formula per il calcolo della varianza:
 
2

 2     2
3
 2     2   2   2  2 
   
 

 
 
3
4
 2 


2
4 2  4  4 2  3 2  3 2  6    

12
12
2
Variabili casuali discrete- La distribuzione binomiale
Una variabile casuale X viene definita binomiale quando permette di ottenere il numero di successi
in n prove, con reintroduzione, tra loro indipendenti e con probabilità costante  di
verificarsi.Questo significa che la probabilità del verificarsi dell’evento E in ogni prova non
presenta alcuna variazione. Tale distribuzione viene indicata con il seguente simbolo :
X  Bn,  
dove n indica il numero delle prove nell’esperimento e  è la probabilità riferita al successo. In n
prove la probabilità riferita a x successi, prescindendo dall’ordine di estrazione, è data dalla
permutazione di x elementi uguali tra loro e dei restanti ( n-x) ancora uguali ma distinti dai
precedenti e per il teorema delle probabilità totali, si ha che :
 n
n x
PX  x    x 1   
con x = 1,2,…….,n
x
 
n
Il valore   è chiamato coefficiente binomiale e rappresenta l’insieme dei casi che presentano x
 x
come successo, mentre  x 1    è la probabilità di avere in n prove x successi e(n-x) insuccessi.
Nel caso in cui il numero delle prove è n =1 si dice che la variabile esaminata è di tipo Bernoulli di
parametro  e la sua distribuzione è del tipo :
27
n x
xi
0
1
totale
p(xi)
1 

1
Questa variabile si dice di tipo dicotomico perché presenta due sole possibilità ,il successo
rappresentato da 1 e l’insuccesso rappresentato da 0. La media di tale distribuzione sarà pertanto :
 x  xi pxi   0  1     1   
e la varianza :
 x2  xi2 pxi    2  0 2 1     12     2   1   
Se il numero delle prove è n, la media e la varianza assumeranno la forma :
 x2  n 1   
in quanto la distribuzione binomiale si può considerare come la somma di n v.c.di tipo bernoulliano
indipendenti tra loro.
Per valori di  vicini a 0.5 la distribuzione binomiale , al crescere del numero delle prove, si
approssima sempre più alla distribuzione normale.
Per dati valori di n e  i valori delle corrispondenti probabilità si trovano già tabulati in apposite
tavole.
 x  n ;
Esercizio
Nel processo produttivo di una fabbrica si è riscontrato che il 10% dei pezzi sono difettosi. Si
calcoli la probabilità che in un gruppo di 5 pezzi scelti a caso :
1) si trovino 2 pezzi difettosi ;
2) nessun pezzo sia difettoso ;
3) non più di due pezzi siano difettosi.
Risoluzione
Nel processo di fabbricazione dei pezzi si possono presentare due casi: i pezzi sono difettosi oppure
non lo sono.Poiché i pezzi scelti a caso sono 5, n= 5 in base a questo valore possiamo costruire la
distribuzione binomiale e trovare le probabilità relative ai casi richiesti. Il numero delle variabili che
dobbiamo prendere in considerazione sono in numero di n+1 cioè in questo caso 6 dal momento che
dobbiamo prendere in considerazione anche la variabile 0 che equivale al caso in cui nei 5 pezzi
esaminati nessuno sia difettoso.Nella produzione si è accertato che la percentuale dei pezzi difettosi
è del 10% e quindi   0.1 mentre 1     0.9 è equivalente alla percentuale dei pezzi non
difettosi.Poiché siamo interessati a conoscere la percentuale dei pezzi difettosi e il numero dei pezzi
scelti è pari a 5 si potranno presentare 0,1,2,3,4,5 pezzi difettosi e la corrispondente probabilità la si
ricava dalla tabella che segue :
Distribuzione binomiale : X  B5,0.1
xi
p (xi )
28
0
1
2
3
4
5
totale
 5 0
 0.1  0.9 5 =1  0.59049=0.59049
 0
 5 1
 0.1  0.9 4 =5  0.06561=0.32805
1
 5 2
 0.1  0.9 3 =10  0.00729=0.0729
 2
 5 3
 0.1  0.9 2 =10  0.00081=0.0081
 3
 5 4
 0.1  0.91  5  0.00009  0.00045
 4
 5 5
 0.1  1  0.00001  0.00001
 5
1
I coefficienti binomiali 1,5,10,10,5,1, si possono ricavare dallo sviluppo del triangolo di Tartaglia
costruito per un esponente n=5:
1 5 10 10 5 1
1 4 6 4 1
1 3 3 1
1 2 1
1 1
coefficienti che compaiono all’interno della tabella corrispondenti a
n=5
Ancora se prendiamo in considerazione lo sviluppo del binomio :
 p  p 5  p 5  5 p 4 q1  10 p 3 q 2  10 p 2 q 3  5 pq 4  q 5
vediamo che in esso compaiono esattamente i valori pi e qi che figurano all’interno della tabella.
Questo spiega perché la distribuzione si chiama binomiale.
Ora possiamo calcolare le probabilità richieste :
P X  x  2  0.0729
P X  x  0  0.59049
P X  x  2  P X  x  0  P X  x  1  P X  x  2  0.59049  0.32805  0.0729  0.99144
La probabilità di trovare non più di due pezzi difettosi è del 99%.
Calcoliamo ora la media e la varianza della distribuzione binomiale precedentemente ottenuta. A
questo scopo predisponiamo la tabella nella quale figurano i calcoli necessari :
xi
p(xi)
xip(xi)
xi2
xi2p(xi)
29
0
1
2
3
4
5
totale
0.59049
0.32805
0.0729
0.0081
0.00045
0.00001
1
 x  xi pxi   0.5 ;
/
0.32805
0.1458
0.0243
0.0018
0.00005
0.5
0
1
4
9
16
25
/
0.32805
0.2916
0.0729
0.0072
0.00025
0.7
 x2  xi2 pxi    x2  0.7  0.5 2  0.7  0.25  0.45
Gli stessi valori potevano essere ottenuti , in modo immediato, usando le formule precedentemente
esaminate :
 x  n  5  0.1  0.5 ;
 x2  n (1   )  5  0.1  0.9  0.45
Variabili casuali discrete – La variabile casuale di Poisson
Quando eventi di tipo discreto vengono considerati in un intervallo continuo ( spazio, distanza etc.),
se si verificano le seguenti condizioni:
l’intervallo di tempo può essere suddiviso in piccoli sottointervalli all’interno dei quali la
probabilità del manifestarsi di un evento è piccola e il verificarsi di due p più eventi è
praticamente nulla ;
- la probabilità del manifestarsi di un evento non subisce modifiche per tutta la durata
dell’esperimento ;
- le probabilità degli eventi nei diversi sottointervallo sono indipendenti tra loro;
allora si dice che siamo di fronte a una variabile del tipo Poisson che è la variabile che viene usata
quando ci si riferisce a eventi che hanno una piccola probabilità di verificarsi.
Questa distribuzione è caratterizzata da un unico parametro :  ( lambda ) che è una costante e
rappresenta il numero medio di osservazioni che si manifesterà in ogni sottointervallo. Tale
parametro costituisce anche la varianza di tale distribuzione.
La funzione di densità di tale variabile è rappresentata da :
-
f x  
x
x!
exp    con x = 0, 1, 2 ….
All’aumentare del valore del parametro  che caratterizza la distribuzione la curva tende a
diventare simmetrica e inoltre tale distribuzione è una distribuzione di frequenze relative o di
probabilità perché la sommatoria è uguale a 1 . Infatti :

x
x 0
x!


x
x 0
x!
exp     exp    
 exp    exp    1

x
 exp  
x!
In presenza di certe condizioni la variabile di Poisson può essere approssimata a una distribuzione
di tipo binomiale e questo risulta di grande utilità perché, in presenza di un numero di prove molto
dal momento che lo sviluppo in serie di

x 0
30
elevato, il calcolo delle probabilità della binomiale diventa molto laborioso.La funzione di densità
della binomiale è data da :
n
n x
P X  x     x 1   
 x
e, se per un valore x fissato e n sufficientemente elevato vale la relazione   n dalla quale si

ricava che :   , la legge di Poisson può servire come approssimazione della binomiale espressa
n
sotto la forma :
 n      
P X  x      1  
 x  n   n 
x
n x

x
x!
exp   
Esercizio
A uno sportello delle ASL vengono serviti in media 2 utenti ogni 3 minuti . Assumendo che il
numero degli utenti che si presentano allo sportello segua una distribuzione di Poisson determinare
la probabilità che sempre nel periodo di tre minuti :
- 1) non si presenti più di un cliente ;
- 2) si presentino 2 clienti ;
- 3) non si presenti nessuno.
Risoluzione
L’evento arrivo dei clienti è di tipo discreto ma si inquadra in un lasso di tempo che è un carattere di
tipo continuo quindi siamo di fronte a una distribuzione di tipo Poisson. Le probabilità richieste
sono le seguenti :
20
21
1) P X  x  1 
exp  2  exp  2  0.1353  0.2706  0.4059
0!
1!
2
2
2) P X  x  2 
exp  2  2  0.1353  0.2706
2!
20
3) P X  x  0 
exp  2  0.1353
0!
Esercizio
Il numero dei neonati ricoverati nel reparto di pediatria di un certo ospedale è pari a 12. Il numero
dei bambini dimessi settimanalmente segue una distribuzione di Poisson con tasso medio di uscita
pari a 2. Trovare la probabilità che vengano dimessi dopo 3 giorni :
1) nessun bambino ;
2) da 2 a 4 bambini ;
3) non più di tre bambini.
31
Risoluzione
Il tasso medio che conosciamo pari a 2 è riferito all’intera settimana. Poiché il problema fa
riferimento alla possibilità di uscita dopo 3 giorni occorre trovare il valore di  che si troverà
utilizzando il seguente rapporto :
3
 0.86
7
Ora possiamo calcolare le probabilità richieste :
  2
1) Px  0 
0.86 0
exp  0.86  0.423
0!
P2  x  4  Px  2  Px  3  Px  4 
0.86 2
0.86 3
0.86 4
 0.86 
exp  0.86 
exp  0.86 
2!
3!
4!
=0.1564+0.0448+0.0030=0.2042
3) Px  3  Px  0  Px  1  Px  2  Px  3 

0.86 0
0.861
0.86 2
0.86 3
exp  0.86 
exp  0.86 
exp  0.86 
exp  0.86 
0!
1!
2!
3!
32