118
PAG G260
Sia AB il diametro di una circonferenza di centro O e sia CD una corda
perpendicolare ad AB che interseca AB nel punto H. Sulla tangente
passante per A scegli un punto E in modo che AE sia congruente a BH.
Da E traccia la parallela ad AB fino a incontrare il prolungamento di CD
in F. Dimostra che il quadrato costruito su CH è equivalente al rettangolo
AEFH.
Costruzione.
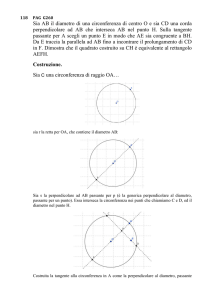
Sia C una circonferenza di raggio OA…
sia r la retta per OA, che contiene il diametro AB:
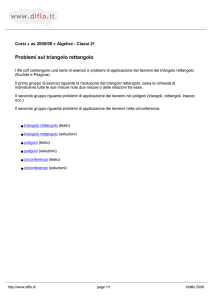
Sia s la perpendicolare ad AB passante per p (è la generica perpendicolare al diametro,
passante per un punto). Essa interseca la circonferenza nei punti che chiamiamo C e D, ed il
diametro nel punto H.
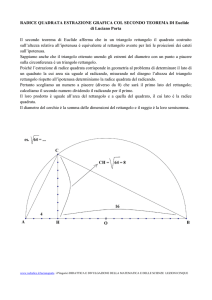
Costruita la tangente alla circonferenza in A come la perpendicolare al diametro, passante
per il punto A, tracciamo sulla retta t il segmento AE avente la stessa misura di BH (E è dato
dall’intersezione tra la circonferenza di centro A e raggio BH e la retta t).
Tracciamo per E la parallela ad AD: essa interseca la retta per CD nel punto F:
IPOTESI: C circonferenza di centro O e raggio OA; AB diametro di C ; AE≅BH
(per costruzione) .
TESI: SHCGI ≗ SAEFH
DIMOSTRAZIONE: Consideriamo il triangolo ABC: esso è un triangolo rettangolo,
Dimostriamo che il rettangolo AEFH è equivalente al quadrato di lato CH. Allo scopo,
consideriamo il triangolo rettangolo ABC, rettangolo in C (è rettangolo in C perché l’angolo
𝐴𝐵̂ 𝐶 sottende il diametro: poiché l’angolo al centro 𝐴𝑂̂𝐵 che sottende il diametro è un
angolo piatto, l’angolo alla circonferenza, che è la sua metà, è retto)
Rispetto al triangolo in esame, il quadrato HCGI è il quadrato costruito sull’altezza relativa
all’ipotenusa mentre il rettangolo AEFH ha lati dati dalle proiezioni dei cateti sull’ipotenusa
(AH è proiezione di AC, 𝐴𝐸 ≅ 𝐵𝐻 -per ipotesi- è congruente alla proiezione del cateto BC
sull’ipotenusa).
Il quadrato ed il rettangolo sono quindi equivalenti per il secondo teorema di Euclide: “In un
triangolo rettangolo (nel nostro caso ABC), il quadrato costruito sull’altezza (nel nostro caso
CH) relativa all’ipotenusa(AB) è equivalente al rettangolo (HCGI) che ha come lati le
proiezioni dei cateti sull’ipotenusa (AH e AE) ”.
Resta così dimostrato che SHCGI ≗ SAEFH