Applnc*xroNr
-§rm$o{s»rNAMscA
mtlL&
m.ffi
Conoscenze
§
Le grandezze
fondamentali di
pressione, temperatu ra
volume massico
e
ll comportamento dei
gas ideali e dei gas reali
Le trasformazioni
Termodinamica dei gas
w Sistemi termodinamici
La Termodinamica è la scienza che studia il comportamento della maè sottoposta a flussi di calore e a variazioni di temperatura,
spesso accompagnate dall'erogazione di una certa quantità di lavoro.
teria quando
: Per sistema termodinamico si intende una definita quantità di mate; ria geometricamente determinata, contenuta allinterno di una superi ficie chiusa.
fondamentali dei
Le trasformazioni termodinamiche dei gas sono riferite all'unità di mas-
gas ideali
sa,
per cui il volume considerato
lJequazione di stato
dei gas perfetti
l=-
ll primo e il secondo
principio della
Termodinamica
Abilità
§
Descrivere le leggi
e le trasformazioni
termodinamiche dei gas,
svolgendo i calcoli relativi
Saper interpretare
i principidella
Termodinamica
Descrivere e saper
interpretare i cicli
termodinamici di Carnot,
Otto, Diesel e Sabathè
Valutare le caratteristiche
e le proprietà del vapore
acqueo
02.1 Termodinamica dei gas
0?.] Trasformazioni
fondamentali dei gas
ideali
02.3 Princìpi della
Termodinamica
02.4 Cicli termodinamici
02.5 llvapore
In pratica il volume massico
minati valori di temperatura
w
Le
è
quello massico:
v [-'l
l-:-
m Lte-l
I
è
il volume occupato da 1 kg di gas a deter-
e
pressione.
coordinate termodinamiche
Lo stato di un qualunque sistema termodinamico, riferito ai gas, è completamente caratterizzato dalla conoscenza dei valori ditre grandezze
fondamentali: pressione .p, temperatura f e volume massico v. Tali
grandezze sono dette coordinate termodinamiche (o variabili di sta-
to) e la relazione che le lega è chiamata equazione di stato.
Lesistenza di uriequazione di stato fa sì che, note due grandezze,laterza
sia univocamente determinata.
w
Gas ideale e gas reale
GIi aeriformi non possiedono né forma né volume proprio, poiché
le loro molecole tendono a diffondersi e a occupare spontaneamente
1o spazio circostante, pertanto possiedono volumi massici superiori a
quelli dei liquidi e dei solidi.
Lo studio teorico della Termodinamica prevede una tipologia di
gas,
cosiddetto ideale, che si basa su alcune ipotesi teoriche riguardanti le
molecole e il loro comportamento.
Il gas ideale o perfetto è un modello di gas che ha le seguenti proprietà:
r
le molecole sono considerate di forma sferica, tutte uguali fra di loro
come massa e occupano un volume puntiforme, quindi trascurabile;
I
L
u
v
li
P
n
f(
p
Applicazioni della Termodinamica
r
gli urti molecolari sono perfettamente elastici, per
r
1e
cui non si hanno dissipazioni di energia;
forze d'attrito fra le molecole e con le pareti del
contenitore sono nulle;
segue perfettamente le leggi della Termodinamica:
le costanti caratteristiche non mutano al variare di
pressione e temperatura.
.
.
11
o
.
Manometro
Termometro
gas reale presenta invece càratteristiche diverse:
o
.
unità 02
le molecole hanno un volume proprio e si scambiano forze di coesione e d attrito;
durante il movimento delle molecole vi sono fenomeni di urto che comportano dissipazione di energia;
il gas reale segue le leggi della Termodinamica in
modo non rigoroso, tuttavia con buona approssimazione, soprattutto se rarefatto;
le costanti caratteristiche variano al variare della
pressione e della temperatura., ma, per semplicità, in
questatrattazione saranno considerate costanti.
(a)
[Il.
Trasformazionifondamentali
dei gas ideali
I
gas subiscono trasformazioni, sia in natura in modo
spontaneo sia nelle macchine a fluido in modo forzato.
(b)
[|tm
a) Sistema term0dinamico a \iolume costante.
b) diagmmma della trasformazione isocora (p,
r).
Particolare importanza è rivestita da alcune trasfor-
mazioni fondamentali la cui formulazione è espressa mediante semplici relazioni tra pressione assoluta,
temperatura e volume massico, e che costituiscono la
base per descrivere ogni comportamento dei gas.
Le trasformazioni fondamentali sono caratterizzate
dal fatto che una delle grandezze termodinamiche che
definiscono lo stato del sistema (principalmente pressione, temperatura, volume e calore) rimane costante
Xintroduzione de1 calore Q provoca llaumento della
pressione e della temperatura iniziali p1 e f1 ai valori
finali p2 e f2. Poiché i.l volume non cambia, si deduce
che 11= ttr.
Per calcolare la temperatura finale si utilizza la seguente relazione:
LT = LT
durante lo svolgimento della trasformazione. I gas che
le compiono sono gas ideali ed esse awengono:
a
a
a
o
a
in cui
volume costante;
pressione costante;
temperatura costante;
senza scambio di calore con llambiente esterno.
a
c,,
=Tz-7,=tr-tr=
Q
mc,
rappresenta la capacita termica massica del
volume costante.
gas nella trasformazione a
a
§§* Trasformazione a volume (ostante iso(ora
La trasformazione isocora, o isovolumica, awiene in
un ambiente chius o in
il gas non può yariare il suo
volume.
ai
Nella figura O2.Ia è rappresentato un contenitore
w
Trasformazione a pressi0ne costante
La figura O2,2a rappresenta un contenitore indeformabile ma dotato di una parete mobile costituita da
uno stantu{fo a tenuta. Anche questo secondo contenitore cilindrico è riempito con la massa z di gas ed è
dotato di termometro e manometro.
pieno di gas ideale con massa m [kg], alla temperatura iniziale f1 ['C] e alla pressionepl [bar]. Se al gas è
fornita la quantità di calore Q [J],la temperatura e la
Lintroduzione della quantità di calore Q provoca un
aumento di tempe ratrra Lt = tz - h= T2- 71, ma non
di pressione allinterno del gas, perché Io stantuffo
mobile consente al gas di espandere per far scendere
pressione nel contenitore aumenteranno.
la pressione allo stesso valore della pressione esterna.
modulo O Termodinamica
Utilizzando.
il
concefl.o di capacità termica massica
sl pxo calcolare la,temperahtra
,2 raggiunta dalla mas_
sa ol gas alla conclusione della
trasfoimazione
termo_
dinamica;
Tr-Tr=tr_ 7r=.9ffico
in cui c, rappresenta la capacita termica
massica [tab.
02.11
delgas nella trasformazione a pressione
costante.
A parità di condizioni di partenza
e di calore intro_
ootto, la temperatura f2 risulla
maggiore nel caso de[_
ra ffaslormazione a volume
costante, minore nel caso
a pressione costante; da questa
consrderazione si deduce che c, >
cr.
j:l:*:9:--l"le.
Dai due
valori di capacità termica massica
derivano
aue grandezze di rilevante significato
nella Termodi_
namrca. La coslante R rappresenta
la diferenza fra le
aue capacitò cpe c, ed è defta costante
"
del gas:
R=co_c,
il rappor to tra le d.ue capaci_
fè d.et1a
fta cp"."^.,:1,:
l* resenta
e cv
costante di poisson:
(b)
ed,
lilDl
c
a) Sisrema termodinami(0
a p.essione costante.
Dl Dragramma derla rrado,maziole
is0bara (r, y).
TABELLA O2.r
_
-
_
Gas e
c
.:
-Capacità termiche n
_
_ , nassiche(p--e.y/ (ostante f,e rapporto *pe, ipi,iirpotii ga5
vapori
Capacità termica massica
a pressione (ostante rp
Capacità termica massica
tk/(ks l0l
IU(kg K)l
Acetilene
CtHt
1,64A
Ammoniaca (vapore)
NH:
2,060
a
volume costante ry
1,330
R=tp-cv
cv
tkJ(ks
Argon
Azoto
Biossido di carbonio
Biossido dizolfo
(loro
0oruro diidrogeno
0oruro di metile
Etano
Etilene
Ar
N2
co2
0,520
1,034
0,842
l:11
t,560
0,s00
0,716
0,87
0,314
0,206
al37
ili
0,50
[1
0,8',I
0,57
cH3ct
0,74
0,5t
(rH+
1,548
1:!"1
0,297
l:l:9
0,653
0,64
1,66
lil
l:1"9
l9i
QHe
0I
0,310
Aria
1,003
,_ (o
4,46
0,37
0,r89
9ll
):le:,1:?
a:1..1.
l:11
1,36
1)s2
9tt
0,17
1:!
l:i9
0,30
l:ll
0,296
1,24
..
Applicazioni della Termodinamica
TA
BEL
LA o2.1
-
(apa(ità termiche massiche r,
ldrogeno
e
rr, (ostante
f
e
unità O2
rapporto ft per i più importanti gas
|17
14,24
10,10
4,14
1,41
À,4etano
(ll+
),253
1,735
0,5r 8
1,30
It,4onossldo di carbonio
t0
1,04r
4,744
4297
1,40
Neon
Ne
1,03
0,618
4,41)
1,61
0,908
0,649
026
1,40
0ssigeno
Protossldo diazoto
Nt)
0,879
0,67
0,209
t,ll
5olfuro dì ìdrogeno
|]rS
0,96t
4,111
4244
1,14
2,A1
1,5)
Vapore
'
aqueo a 100 "C
HrO
Trasformazione a temperatura costante
Una trasformazione che ar,wiene a temperatura cos/a,1re è detta isoterma.
La legge di Boyle - Mariotte afferma che, a temperatura costante,la pressione esercitata da un gas ideale varia
in ragione inversa al volume unitario, pertanto, durante
la trasformazione il prodotto della pressione per il volume massico rimane costante:
?/=cost a
T=cost
-1,32
Trasformazione adiabatica
Una trasformazione che al.viene senza scambiare ca
lore con llambiente esterno è detta adiabatica. Nel cor
so di questa trasformazione, i flussi entranti e uscenti
di calore sono nulli, mentre variano pressione, volume
e temperatura.
Il
sistema è termicamente isolato. Gli scambi dènergia
con l'ambiente sono costituiti solo dal lavoro che può
essere positivo se eseguito dal gas (come nel caso di unèspansione) oppure negativo se subito dal gas (come nel
caso di una compressione). La formula delladiabatica è:
Da tale formula si può ricavare la seguente uguaglianza:
Plyt=
p2y2 = P3y3...
p
fesponente k è
r.,r
= cost
il rapporto tra crlc, riportato
nella
tabella O2.1. Nel piano (p,y) la Iinea termica delLa-
Il
grafico dell'isoterma riportato nel diagramma
(p,v) della figura O2.3 ha la forma di un iperbole
equilatera.
diabatica è una curva decrescente, asintotica agli
assi coordinati e simile a quella della famiglia delle
iperboli [fig. 02.4].
IEE
DE
Gmfco de l'isoterma su plano(p,y): ailasf0rmazi0ne
ha l2ndamento di un'lperbo e eqLll atera riferÌta agll assl.
Diagramma della linea di trasformazione adiabatica
" ' ontono
.
o- e
ree de le a tre trasformal 0n
modulo O Termodinamica
Il lavoro del
ew Trasformazione politropi(a
gas è:
positivo (l > 0), se 1a linea è percorsa nel senso dei
volumi crescenti; in questo caso il gas esegue una
espansione e si ha lavoro motore;
negativo (I < 0), se la linea è percorsa nel senso
dei volumi decrescenti; in questo caso il gas subisce una compressione e si ha lavoro resistente.
Le quattro trasformazioni fondamentali possono essere considerate casi particolari di una generica trasformazione politropica, la cui espressione è:
p v. = cost
infatti:
.
.
o
penn = I si ottiene la relazione delf isoterma;
pet m=O (v0 = 1) si ottiene la formula delfisobara;
per m = /c si ottiene l'adiabatica.
ffi
Equazione di stato dei gas
*
La prima legge di Gay - Lussac dichiara che riscaldando o rafreddando una massa di gas ideale a pressione costante, il suo yolume aumenta o diminuisce
linearmente al yariare della temperatura t ["C] secon-
perfetti
do la seguente formula:
Le variabfi che definiscono lo stato di un gas ideale
sono legate dalla seguente relazione, detta equazione
di stato dei gas perfetti:
y=%(1+0r)
dove:
pv=RT
r
o
o
in cui:
r T è espressa in K;
o v è espresso in m3/kg;
r p è espressa in N/m2;
o À = (c, - c,) è espresso in J/(kg K).
ffi
LeggidiGay-Lussac
Vs è il volume della massa di gas a 0 [oC];
Vè il volume a f ['C];
cr è
il
coe{ficiente termico di dilatazione volume-
trica dei
gas.
La seconda legge di Gay - Lussac afferma che r!
scaldando o rafreddando una tnassa di gas ideale a
volume costante,la sua pressione aumenta o diminuisce linearmente al variare della temperatura t ["C]
secondo la seguente
Lavoro compiuto da un gas
Nella figura O2.5 è rappresentata una trasformazione politropica fra i punti I e 2.larea compresa fra
la linea termica della trasformazione (dal punto 1 al
punto 2) e la linea delle ascisse rappresenta il lavoro
compiuto dal gas.
formula:
p= po$+at)
dove:
r
r
.
ps è il volume della massa di gas a 0
pèilvolumeaf ['C];
0 è il coefficiente termico di
trica dei
'C;
dilatazione volume-
gas.
Il coefficiente termico di dilatazione volumetrica assume valore o = 0,0366 [1/'C] per tutti i gas e rimane
pressoché costante al lzriare di pressione e temperatura.
m.ffi
m
Principi della Termodinamica
Primo principio della Termodinamica
i Il primo principio della Termodinamica afferma
: che lbnergia non può essere creata o distrutta, ma so= lo trasformata.
Esso può essere enunciato ne1 seguente modo:
0E
[area sottes alla linea termica rappresenta
fraipumile2.
il
avoro del
gm
in un si-
stema termodinamico che scambia energia con lbsterno,la somma algebrica del calore, del layoro e dellbnergia interna è pari a 0.
Applicazioni della Termodinamica
lespressione analitica
è
la seguente:
AQ=AI+^LI
in Termodinamica poiché è assunto come termine di
riferimento per ogni altro ciclo. Carnot, ideando questo ciclo, si era posto i due obiettivi seguenti:
in cui:
.
r AQ rappresenta il calore scambiato dal gas;
o Al è il lavoro fornito (Al > 0) o assorbito (Al, < 0);
o A U è la variazione di energia interna:
LU = c, lT6,o1" - T;,;,;o1"\
o
quindi,la conf".-u.h" luro.o a aalore sono forme
di energia che possono trasformarsi luna nelllaltra. Se si
I1 ciclo
Si ha,
ottiene dal sistema una quantità di lavoro l, introducendo iÌ calore Q, si possono avere tre casi di seguito esposti.
r
o
o
1 = Q: l'energia termica è stata completamente trasformata dal gas in energia meccanica; i valori della
pressione e della temperatura sono invariati.
Q > I: a pari entità di lavoro I richiesto, lèsubero
di energia termica fa sì che il termometro segnali
Iaumento di temperatura; una certa quntità di ca
lore resta immagazzinata all'interno del gas e diventa parte del suo patrimonio energetico;
Q < I: il gas esegue il lavoro richiesto ma a prezzo
di un suo raffreddamento; le molecole hanno doiuto attingere calore dalle loro riserve energetiche
interne per poter syolgere il lavoro richiesto.
r Secondo prin(ipio della Termodinamica
I vari enunciati, fra loro equivalenti, del secondo
principio della Termodinamica, afermano che non
è possibile trasformare tutto il calore Q in lavoro poiché se cosi Josse, si realizzerebbe il moto perpetuo.
Un possibile enunciato è il seguente: non è possibile
eseguire una trasformazione ciclica chiusa la quale re'
alizzi come unico risultato la totale trasformazione in
lavoro di tutto il calore proveniente da una sola sorgente di calorc a temperatura costante.
La trasformazione ciclica awiene attraverso una
successione di trasformazioni compiute dal gas per
raggiungere Io stato finale. Nelle macchine termiche
comuni 1o stato finale coincide con quello iniziale e il
ciclo si definisce chiuso.
note Ie temperature 72 e 71 delle due sorgenti di
calore che fungono rispettivamente da alimentatore e da scarico, individuare il ciclo di trasformazione che consente di raggiungere il massimo rendimento possibile;
scoprire se il valore del rendimento del ciclo è influenzato dalla natura del gas ideale impiegato.
di Carnot consiste in quattro trasformazioni,
due adiabatiche e due isoterme tflg. 02.61.
ffi
[iclo termodlnamlco diCatnot.
Nel tratto 1-2 il gas è compresso adiabaticamente dalIa temperatura 11 fino a raggiungere la temPeratura 72;
nel tratto 2-3 alviene un espansione isoterma con fintroduzione della quantità di calore Q2; poiché ?, = T,
tutto il calore fornito si è trasformato in lavoro (AU= 0).
Nel tratto 3-4, finita Ia somministrazione di calore,l'espansione prosegue adiabaticamente e Ia temperatura
si abbassa fino al valore ?4; nel tratto 4 1 avviene una
compressione isoterma che riporta il gas alle condi-
zioni iniziali del punto 1, poiché 7+ = Tt deve essere
sottratta la quantità di calore Q1 che è uguale al lavoro
fornito dallèsterno per compiere la compressione.
Si ricorda che
.,
Ciclo
Cicli termodinamici
il primo principio della Termodinami
ca si esprime con la relazione:
aQ=
-
ar+nu
= Tini"iol" come ar.viene nella trasformazione isoterma (^U = 0),
il secondo principio della Termodinamica diventa:
e che LU =
[Il.''i,
unità O2
cu
(Tfro1"
T ini"1o6); se T7not"
diCarnot
Lo studioso Sadi Carnot presentò nel 1824 lbmonimo
ciclo, scegliendo fra le tante le due trasformazioni che
offrivano i1 miglior rendimento, f adiabatica e l' isoter'
ma.ll ciclo di Carnot riveste una speciale importanza
t
^Q=Ar
Tutto il lavoro fornito durante un isoterma si trasforma in calore che deve essere sottratto, mentre tutto
calore fornito si trasforma in lavoro.
il
modulo O Termodinamica
Rendimento del ciclo di (arnot
II rendimento di un ciclo può essere
espresso con la
seguente relazione:
n=
,Q,!=Q,-Q, =1-Q,
Q,Q,
Nel caso del ciclo di Carnot si ha:
lì=l-l
,7.
T.
da cui si deduce che il rendimento del ciclo teorico
di Carnot, che impiega un gas perfetto, dipende solo
dal rapporto fra le temperature, inferiore e superiore,
e non dal gas impiegato.
Da quanto appreso nello studio del ciclo di Carnot, si
possono indicare i due principali metodi per aumen
tare il rendimento di un ciclo e, di conseguenza,
durre i consumi e limpatto ambientale:
.
.
continua di lavoro queste macchine ripetono i1 ciclo
in rapida successione, rinnovando il fluido al termine
di ogni ciclo.
Tutti i motori, sia alternativi sia rotanti, realizzano come prima trasformazione :una compressione che, con
buona approssimazione, è assimilabile a un adiabatica. La compressione preventiva dei gas è decisiva per
raggiungere rendimenti elevati.
La seconda trasformazione è la combustione che avviene a volume costante o a pressione costante o con
soluzione mista, a seconda dei cicli e del tipo di combustibile adoperato. La trasformazione successiva è
7'espansione, dtrante la quale si genera il trasferimento di energia dai gas caldi e compressi allbrgano mobile, collegato con l'albero motore uscente. fultima
trasformazione èla sottrazione di calore ottenuta mediante espulsione dei gas esausti.
ri-
raggiungere la massima temperatura interna
compatibilmente con le sollecitazioni termiche
ammissibili dagli organi delle macchine (infatti il
rendimento cresce con l'innalzamento della temperatura T2);
rilasciare i fluidi di scarico alla più bassa temperatura possibile, trasformando in lavoro una sempre
piir alta percentuale del calore posseduto dal gas;
Ìa presenza del calore residuo e1 negli scarichi è
a tutti gli effetti uno spreco di energia; il secondo principio della Termodinamica insegna che il
calore residuo non può essere annullato del tutto,
d altra parte conferma che llabbassamento della
temperatura I dei fluidi di scarico e il riutilizzo
del loro calore Q1 possono dare concreti migliora,
menti al rendimento delle macchine termiche.
:r.,..:
Ciclo
0tto - Beau de Rochas
È il ciclo utilizzato nei motori alternatiyi ad accensione comandata e porta i nomi dellideatore, Alphonse
Beau de Rochas, e del costruttore del primo motore,
Nikolaus Otto.
I motori ad accensione
comandata sono detti comunemente a scoppio, hanno laccensione innescata
mediante scintilla e sono alimentati principalmente
a
benzina.
Il ciclo Otto - Beau de Rochas è composto da quattro
trasformazioni, come riportato nella ftgura O2.7:
a
o
.
o
una compressione adiabatica fra i punti 1 e 2;
Q1 a volume costante fra
Ì'introduzione del calore
un espansione adiabatica fra i punti 3 e 4;
lèspulsione del calore residuo Q1 avolume costante fra i punti 4 e 1.
... Principali cicli termici utilizzati nei m0t0ri
a
combustione interna
I motori a combustione interna producono
lavoro
meccanico trasformando lènergia chimica posseduta
dal combustibile in calore. Nei motori alternativi la
combustione awiene in una camera a diretto contatto
con lbrgano mobile (pistone).
La composizione chimica del gas presente internamente al motore cambia: infatti, all'ingresso si ha la
miscela di aria e combustibile; in uscita si hanno fumi
costituiti dai gas combusti. Dato che la miscela aria combustibile può cedere 1a propria energia chimica
una volta sola, il fluido è espulso al termine di ogni
ciclo per essere sostituito. Per ottenere I'erogazione
ffi
i
punti 2 e 3;
Ciclo Otto teorko.
Applicazioni della Termodinamica
unità 02
ffi (ido Diesel teorico
Ciclo Otto reale
Nella realtà il ciclo si diferenzia da quello ideale poiché la combustione non può essere istantanea e 1e valvole di aspirazione e scarico non si aprono e chiudono
esattamente nelle posizioni limite del pistone. Ino1tre,
per aspirare l'aria fresca e per espellere i fumi, occorre
fornire energia.
Il ciclo reale è tracciato sperimentalmente mediante
un indicatore che rileva l'andamento della pressione
ne1 cilindro a1 variare della corsa del pistone. Il ciclo
reale è comunemente detto diagramma indicato o
ciclo indicato [fig. O2.8], proprio perché rilevato grazie alliapparecchiatura nota come indicatore.
il ciclo impiegato nei grandi motori marini alternativi ad accensione spontanea alimentati a nafta. Esso
È
porta il nome
de1 suo inventore, Rudolf Diesel. Nei motori ad accensione spontanea Ia combustione s'innesca
da sola, senza bisogno delia scintill4 grazie agli elelati
valori di pressione e temperatura raggiunti in camera
di combustione. Il ciclo Diesel è composto da quattro
trasformazioni, come riportato nella figura O2.9:
.
.
r
r
una compressione adiabatica fta i punti 1 e 2;
l'introduzione del calore Q2 a pressione costante
fraipunti2e3;
uriespansione adiabatica fra i punti 3 e 4;
l'espulsione del calore residuo Q1 a volume costan-
tefraipunti4el.
Perdite dspetto al ciclo teorìco
Perdite all'aspirazione e allo sca co
Ciclo reale
PMS
ftm
PI\,II
funfronto fra (iclo 0tt0 teori(0 e indicato.
Dalllosservazione dei due cicli sowapposti emergono
m
Cklo DÌeselteoriro.
le seguenti indicazioni:
o
e
l'area del ciclo reale risulta inferiore a quella del ciclo ideale;
nel ciclo reale compaiono due aree orizzontali
adiacenti disposte, rispettivamente, al disotto e al
disopra della quota indicante Ia pressione atmosÈrica, che rappresentano i lavori di pompaggio in
aspirazione
e
in scarico.
Ciclo Diesel reale
Anche in questo caso il ciclo reale occupa un'area inferiore rispetto a quella occupata dal ciclo ideale e riporta le due aree inferiori a sviluppo orizzontale relative ai lavori di pompaggio in aspirazione e in scarico
lfi9. 02.10].
Oltre a occupare una superficie minore, il ciclo reale presenta anche delle diferenze di forma rispetto a1
ciclo ideale da cui deriva, dovute principalmente alle
f
Perdite rkpetto al ciclo teorico
Ciclo indicato
seguenti cause:
r
lniezione del carburante
Perditealì'aspirazioneealloscarico
le trasformazioni di compressione e di aspirazione
sono politropiche anziché adiabatiche;
a la
combustione non awiene istantaneamente,
.
quindi non è rigorosamente isovolumica;
fistante di inizio della combustione alwiene prima
.
vi sono perdite di pressione dolrrte al prolungamen-
che il pistone abbia raggiunto
il PMS;
to del tempo di apertura della valvola di scarico.
In linea di massima, nel ciclo Otto si raggiungono
pressioni di 35 -;-40 bar.
PMs
[ffi
PMI
Confronto fra il cic 0 Diesel ideale e indicato.
v
modulo O Termodinamica
La diferenza tra i cicli ideale
e reale in termini di forma e di valori numerici sono allincirca le stesse giàr
incontrate per il ciclo Otto. Le caratteristiche specifi-
che del ciclo Diesel reale sono
o
.
1e
seguenti:
la combustione non è rigorosamente isobara
a
causa del moto dello stantuffo che determina variazioni di pressione;
le perdite per pompaggio in aspirazione hanno
un incidenza minore dato che, a diferenza del ciclo
Otto, nei cicli Diesel e Sabathè la valvola a farfalla
nel condotto di aspirazione non regola la portata,
ma crea un efetto di strozzamento.
0rf,l
Ci(lo Sabathè reale (o indicato); nella zona superiore si ri(onoscon0
le due fasi della combustione isovolumlca e isobara.
s+ry
È
(iclo Sabathè teorico
il ciclo impiegato nei motori alternativi di piccola
e
media dimensione a combustione spontanea alimentati
a gasolio. Esso porta il nome delllideatore, Sabathè. È un
ciclo intermedio fia il ciclo Otto e il ciclo Diesel; llintroduzione di calore è sdoppiata in due fasi successive.
Il ciclo Sabathè è anche chiamato ciclo Diesel veloce,
ed è composto da cinque trasformazioni, come riportato nella figura O2.I'l:
r
.
.
r
r
una compressione adiabatica fra i punti
1e
a
m.ffi
volume costan-
tefraipunti5el.
llvapore
I vapori sono aeriformi che si trovano in configu-
2;
una prima introduzione di calore a volume costante Q2' fra i punti 2 e 3;
una seconda introduzione di calore a pressione costante Q2" fra i punti 3 e 4;
uriespansione adiabatica fra i punti 4 e 5;
fespulsione del calore residuo Q,
Nei cicli Diesel e Sabathè si raggiungono pressioni di
60 -70 bar e anche superiori, se il motore dispone
dei piìr moderni apparati di iniezione. In alcuni casi
il picco può raggiungere, per brevi istanti, valori anche doppi.
razioni termodinamiche non lontane dal punto di
liq uefazione.
Il
vapore piu importante in natura, come nel campo
industriale, è il vapore acqueo. Tuttayia esistono altre
sostanze che ricoprono notevole importanza merceologica sia allo stato liquido sia allo stato aeriforme: ammoniaca, anilina, vari tipi di alcoli, eteri, idrocarburi,
cloruri e diverse sostanze gassose. Molti sono presenti
sul mercato anche in fase liquida, come l'aria, il biossido di carbonio, lbssigeno, Iazoto e i GPL, per cui è
fondamentale conoscerne il comportamento nel mo-
mento del passaggio di stato.
In questa sede lo studio verte esclusivamente sul vapore acqueo, tenendo comunque presente che tutti i
vapori seguono gli stessi procedimenti di generazione
a partire dallo stato liquido e rispettano le stesse regole fisiche generali.
liIIIl
ffi
(iclo Sabathèteorico.
Ciclo Sabathè reale
Il
ciclo Sabathè reale assume una forma intermedia
fra quelle dei cicli Otto e Diesel, come riportato nella
figura 02.12.
vapore a(queo
La generazione del vapore a partire dallo stato liquido
può awenire secondo due diverse modalità.:
a
c
evaporazione;
ebollizione.
Levaporazione è il lento fenomeno di passaggio
di stato da liquido ad aeriforme riguardante solo la
Appìicazioni della Termodinamica
superficie libera del liquido. È una trasformazione
che awiene solitamente a bassa temperatura.
I-evaporazione consiste nel passaggio delle molecole
d acqua allo stato di vapore in modo graduale e invi
sibile ad occhio nudo, fin da11e piìr basse temperature,
anche prossime allo zero; è per questo motivo che anche in inverno una pozzangheru dacqua si asciuga in
tempi piìl o meno lunghi, in funzione della temperatura e dell umidità atmosferica.
Lebollizione è il passaggio di stato da liquido ad aeriforme e ar.viene in tutta la massa liquida in modo
tumultuoso. Per ogni valore di pressione essa s'innesca al raggiungimento di una particolare temperatura
detta temperatura di ebollizione o di saturazione.
Riscaldando Jiacqua contenuta in una pentola aperta,
TABELLA 42.2
- Pressioni,
e
massr(l
lèvaporazione s'intensif,ca man mano che Ìa temperatura cresce, finché il liquido raggiunge la temperatura di ebollizione; alla pressione atmosferica essa vale 100 "C. Da tale momento lèvaporazione evolve in
ebollizione, la massa entra in uno stato di agitazione
e la trasformazione awiene in tempi molto più brevi,
con 1a formazione di bolle di vapore alllinterno della
massa liquida.
Temperatura di ebollizione
La temperatura di ebollizione dellacqua dipende
dalla pressione cui è sottoposta la massa liquida. Nella
tabella 02.2, riferita all'acqua distillata, sono riportati
i valori di temperatura di ebollizione in funzione della
pressione assoluta nel circuito.
e del
Volume massico
Ptessione
Iemperatura
Ibarl
rc1
Volume massiro
lm:/kgl
Liquido saturo
unità O2
Presione
Temperatura
tbarl
rc1
Vapore saturo
Im:/kg]
Liquido saturo
Vapore saturo
0,10
x'10-l
14,7
20
)12
1,17
x
10-3
1,02,(
l0 r
1,65
)5
224
1,20
x
I
0-3
80
x
1,02
x
10-r
s)3
30
234
1,21
x
1
0-3
67
x 10-l
76
1,03
x
10-3
3,99
35
)43
1,23
\
I0-l
57
x
10-r
0,5
81
1,03
x
1
0-3
1qq
40
250
1,25
x l0-r
50
x
10-3
1
99
1,04
x 0-l
1,69
50
)64
1,29
x
10-3
39
x
I
1,16
60
)76
1,32
x 10-l
32
x 0-l
0,89
70
286
1,35
x 0-l
27
x
0,1
46
1,01
0,2
60
0,3
69
0,4
1
1
0-r
0-3
1,5
1ì1
1,05
x
'10-3
)
124
1,06
x
10
2,5
127
1,07
x
10-3
0,72
80
295
1,38
x
0-3
24
x 10-l
j
134
1,07
x
I
0-r
0,61
90
301
1,42
x I0-r
20
x
10-3
139
r,08
x 0-l
0,52
100
311
1
n-t
18
x
10-3
x 0-r
3,s
3
1
x
,45
1
^
1
1
1
0-3
144
1,08
0-3
4,46
110
318
1,49
x 10-l
16
4,5
148
1,09 x 10-l
0,41
120
,5
1,53
x 10-l
14x 10-l
5
1s2
1,09
x 10-l
0,37
130
331
1,58
x
10-r
13
x
10-r
159
1,10
x
0,32
140
337
1,61
x
10-3
1'l
x
1
7
lb5
l,l0 r l0-l
0,21
342
1,66
x 0-l
1
10
x 0-l
I
170
1,11r I 0-l
0,24
160
347
1,71
x
10-3
9l
x
'10-4
9
115
1,12
x l0-r
4,21
110
352
1,77
xrc-3
84
x
10-4
t0
180
l,l3 x l0-r
0,19
357
1,84
x l0
r
/5
x 10+
4
6
I
10-r
1)
188
1l4x
'10-3
14
195
1,15
x
10-3
T5
198
1,1 5
'1,17
17,5
)06
'r50
'180
1
0-3
1
0,
t6
190
36)
1,92
x 10-l
67
x 10+
0,
t4
200
366
2,04
x 10-l
58
x 10r
x 10-l
0,13
210
370
2,21
x 10-l
50
x
x 10-l
0,11
1
0-4
modulo O Termodinamica
(alori di vaporizazione
Si definisce vapore saturo secco quello che si trova nella condizione limite quando anche liultima
goccia di liquido si è appena trasformata in vapore:
e dicondensazione
Le trasformazioni di vapoizzazione e di condensazione sono di tipo isotermobarico, dato che si svolgono interamente a pressione e temperatura costanti.
In pratica, fornendo calore alliacqua, la temperatura
aumenta fino al yalore di ebollizione; da questo punto
in poi liacqua si trasforma in vapore e il calore Q" fornito non aumenta la temperatura e la pressione, ma
serve unicamente al passaggio liquido-vapore.
entrambi hanno le condizioni di pressione
liquido saturo quel1o che si troya nella
condizione limite quando sta per iniziare l'ebollizione con la formazione delle prime bol1e di vapore.
Si definisce vapore surriscaldato quello non saturo
che si trova a una temperatura superiore alla tempe-
ratura di ebollizione corrispondente
La trasformazione si svolge a pressione e temperatura
costanti e il calore totale sottratto è pari esattamente
cui
è
modifica pres-
pore diventa surriscaldato.
sione e temperafura del vapore.
Alla temperatura di 100 'C, il calore latente di vaporizzazionel condensazione dell'acqua distillata vale
circa 2265 kJ lkg.
foperazione in genere è di tipo isobarico, per cui il
calore unitario di surriscaldamento Q,. rispetta la
formula del calore a pressione costante:
Analogamente, a 0 oC e a pressione atmosferica, può
q,,,=cr(tr,_t_*)
verificarsi il passaggio acqua-ghiaccio (solidificazione), oppure ghiaccio-acqua (fusione). Anche in
queste trasformazioni di stato 1a temperatura rimane
costante e il calore latente di fusione e solidificazione
vale circa 334 kf/kg.
Nella relazione compare la capacitàL termica massica cr,
mentre in parentesi vi è la differenza tra. la temperatura
di fine surriscaldamento tfn e la temperatura di inizio
surriscaldamento, che è pari alla temperatura di evaporaziolJe teyap.
Condizioni di saturazione
Il valore di c, è fortemente influenzato dalla pressione e
dalla temperatura; occorre pertanto calcolare un valor
Si definisce vapore saturo
urnido il vapore che si trova in presenza del suo liquido in condizioni di equilibrio termodinamico. Il liquido e il vapore sono en-
medio di c, relativo alJ'ntervalJo (tp- teua).
Nella tabella O2.3 sono riportati i valori di c, ricavati
trambi alle medesime condizioni di pressione e di
sperimentalmente da Knoblauch e fakob in funzione
della pressione e della temperatura.
temperatura.
TABELLA 02.3
e della
-
a1la pressione
sottoposto.
Somministrando calore alla massa formata da vapore
saturo secco,la temperatura ricomincia a salire e i.l va-
al calore Q, di vap orizzazione.
è detto latente poiché non
di tem-
Si definisce
Un comportamento del tutto analogo si ha durante
la condensazione, fenomeno inverso dellèbollizione.
II calore Q,
e
perafura.
Andamento della (apacità termica massica (p delvapore acqueo [U/(kg K)i in funzione della pressione assoluta
temperatura
Capa(ità termica massica (p del vapore a(queo IkJ/(kg K)]
Presslone
1
2
4
r= 150'(
1,934
2,001
),156
r=
200
"(
1,934
1,988
t=
250
"t
1,938
f=
300
"i
t=
l=
400
6
8
10
12
2,101
2)19
),34
) 4qq
2,658
1,984
),47)
2,151
),D]
2,311
1,94)
i,988
2,059
2,114
2,164
350 "C
1,959
1,991
),059
2,1A6
"(
1,980
2,013
2,068
),114
assoluta lbar]
20
14
16
18
2,386
),461
2,549
2,658
))19
)26s
DAz
),348
2,694
),449
),143
2,185
)214
2,24
))13
2,302
2,33)
2,143
),117
2)0)
2)22
2)48
)269
2,290
Applicazioni della Termodinamica
Titolo delvapore
All'interno del contenitore che ospita vapore allo stato saturo umido deve essere presente anche la fase liquida. La massa fluida si presenta in forma di miscela,
Ia cui composizione varia fra due valori estremi: 100%
liquido e 0% vapore; 0% liquido e 100% vapore. Nel
primo caso si è in presenza di solo liquido saturo, nel
second,o di tapore saturo secco.
Con riferimento a I kg di miscela, si definisce titolo
del vapore x i1 rapporto tra la massa di vapore saturo umido rz, e la massa totale, somma delle masse di
vapore saturo ,rr, e di liquido m1:
mt+mt
Per esempio se .r = 15%, il chilogrammo di miscela
è formato da 0,150 kg di vapore saturo umido e da
0,850 kg di liquido; al liquido saturo è stato somministrato
il
15% del calore di vaporizzazione
e".
Entalpia
fentalpia h considera tutto il contenuto energetico di un
sistema. Se riferito a 1 kg di vapore, misura sia il calore
contenuto sia lènergia dowta alla pressione che coskingono il chilogrammo di lzpore a occupare il volume y.
Il calore sensibile
acqua da 0 "C
a1
Q" eleva la temperatura di i kg di
valore di saturazione (ebollizione),
pertanto si possono fare Ie seguenti considerazioni:
o
r
o
lèntalpia dell'acqua a 0 'C vale h = 0;
lèntalpia del liquido saturo vale h = Q;
l'entalpia del vapore saturo umido con titolo x vale:
r
lèntalpia del vapore saturo secco vale:
o
unità O2
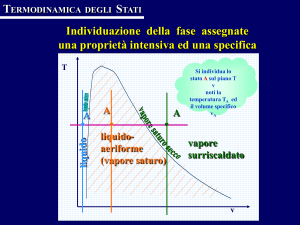
Sulle ordinate sono riportati i valori delle pressioni
di saturazione, corrispondenti alle rispettive temperature di ebollizione, e sulle ascisse i relativi volumi
massici zl per il liquido saturo e r.,r, per il vapore saturo secco. I punti individuati da ogni coppia di valori
formano due curve di saturazione denominate curva limite del liquido saturo (o linea di saturazione
inferiore) e curva limite del vapore saturo secco (o
linea di saturazione superiore). La curva di sinistra
avente ,r = 0 si presenta assai ripida, poiché iI volume
massico dellacqua varia di poco al variare di pressione e temperatura, si mantiene parallela all'asse delle
ordinate fino a una pressione di circa 100 bar. La curva di destra, avente r = 1, decresce al crescere dei volumi massici, con andamento quasi iperbolico nel suo
tratto inferiore.
Larea interna alle due curve
limiti è quella
del vapore
saturo umido con l'indicazione dei relativi titoli, mentre l'area esterna sulla destra della linea limite supe-
riore
è quella relativa aÌ vapore surriscaldato.
Esaminando iI grafico ne1 senso delle pressioni crescenti, si nota che la differenza tra i volumi massici
dell'acqua e del vapore saturo secco tende a ridursi.
Nel punto di convergenza delle due curve limite, detto punto critico K corrispondono la pressione critica
oC
e
P«= 221,?9 bar,la temperatura critic a tK= 37 4,1
il volume massico critico y(= 3,09 x i0-3 m3/kg.
II punto critico definisce uno stato fisico particolare
per il quale il liquido saturo si trasforma in vapore
senza ulteriori somministrazioni di calore. Per temperature superiori a quella critica ,K per quanto si aumenti la pressione non è possibile ottenere la condensazione del vapore.
h=es+xed'
h=e,+e";
lèntalpia del vapore surriscaldato vale:
ft= Q+ Q"+ Q,,.
i\lx
Diagrammi p,u del vapore acqueo
I vapori non seguono le leggi dei
gas ideali;
Àr§
colare:
a
.
la costante k non può essere definita con un valore
unico poiché 1e capacità termiche co e c, variano
sensibilmente con la pressione e la temperatura;
I equazione di stato dei gas perfetti p v = R T non
può essere applicata in quanto non esiste una co-
stanteRperivapori.
{t\ ,IN
(-\ì
50
È
La figura O2.13 illustra il diagramma di Andrews che
riporta le curve rappresentative per il vapore acqueo
sul piano p,y.
\
ÀÈ'.'
in parti-
0
II,IE
\
§
{r'.'
200'c
:---
:lqo
"^
{qr-
ì"ì:-\ì
0,01 a,a2 0,03
Diagramma di Andrews per
i
0,04
vap0re acqueo.
vlmYkgl
modulo O Termodinamica
(iclo Rankine
Negli impianti termici di grandi dimensioni si utilizza
il vapore surriscaldato ad atta pressione per aziona
re le turbine che, collegate agli alternatori, producono
energia elettrica.
un riscaldamento (tratto 2-3) per portare il liquido a livello di saturazione, pronto per iniziare 1èbollizione;
un riscaldamento che fornisce il calore latente di
vaporizzazione (tratto 3-4), trasformando il liquido in vapore saturo secco;
un'espansione adiabati.ca in turbina (tratto 4-5),
nel corso della quale il vapore cede gran parte del,
la sua energia alla turbina in rotazione [fig. 02,15];
una condensazione isotermobarica (tratto 5-1)
con sottrazione di calore dentro appositi condensatori; il condensato è estratto da pompe di estrazione che lo inviano alle pompe di alimento.
ItfE
Ci(10 idea e di Rankine sul diagramma p,rr.
Il ciclo di Rankine
è
costituito dalle seguenti trasfor-
mazioni [fig. O2,14]:
a
una compressione dellacqua con pompe di alimento
(tratto i-2) in cui la pressione può superare i 150 bar;
EE
Palettatura dl una turbina a vap0re.
rISr
I
1
Dare la definizio ne di Termodinamica.
(max 30 parole)
3.
lsoterma, a lemperatura costante:
4.
Adiobatica, senza scambio dicalore:
6l
Scrìvere lEquazione di stato dei gas perfetti, specificando il significato delle variabilì presenti e la loro
unilà di misura.
2l
Quali sono le tre grandezze deite coordinate
modinamiche o voriabili di stota'|
ter
l.
2.
7l
5crivere l'enunciato della
8l
S.riu"r" l'enunciato della seconda leqqe di Cay-
prira
legge diGay Lussac.
3.
3l
Un gus si dice ideole o perfeno quando ha le seguenti proprietà.
I
.
Le molecole sono considerate dÌ
,,,'..,,,,'.,,,,''..,''.,
2.
3.
e
lorrna
Lussac.
tUtte
Gli urti molecolarisono perfettamente
Le forze
.................................
d'attrito fra le molecole e con le pareti del
contenito.e sono....
4.
I
Segre oerfettanente e eggidel.a
quuttro trurformazioni fondamentali possono essere considerate casi particolari di una generica trasformazione politropica la cui espressione è:pvm = cost.
4
E
Le
Vero
n
Fa
so
9
[
tt primo princlpio della Termodinamica afferma
che l'enerqia non può essere creata o distrutta, ma solo
trasformata.
E
Vero
!
Falso
I
101
ll secondo princ;pio della Termodinamica
che non è possibile trasformare tutto il
5l
Precisare il valore assunto dall'esponente m nelle
quattro trasformazioni fondamentali dei gas ideali.
f.
isocoro, a volurne costante:
2,
lsobara, a presslone costante:
Otto - Beau de Rochas
.....................................
poÌché se così fosse, si realizerebbe il
11
2.
afferrra
I
Comptetare la tabella sottostante, riportando
per iquattro cicli termodinamici, le caratteristiche e i
campi di impiego.