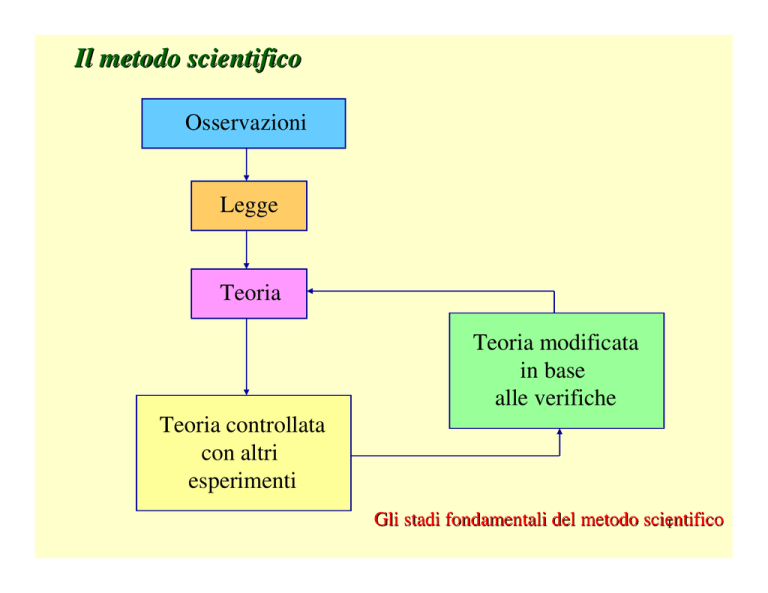
Il metodo scientifico
Osservazioni
Legge
Teoria
Teoria controllata
con altri
esperimenti
Teoria modificata
in base
alle verifiche
Gli stadi fondamentali del metodo scientifico
1
Leggi ponderali
• Legge della conservazione della massa (Lavoisier)
La massa totale di un sistema reagente non varia
• Legge delle proporzioni definite (Proust)
In qualunque composto il rapporto fra le quantità in
peso degli elementi costituenti è definito e costante
• Legge delle proporzioni multiple (Dalton)
Quando due elementi possono combinarsi insieme in
rapporti ponderali diversi per dare diversi composti, le
quantità di uno di essi che nei vari casi si combina con la
medesima quantità dell’altro stanno fra loro in rapporti
espressi da numeri interi, generalmente piccoli.
2
Legge delle proporzioni multiple
g di azoto
g di ossigeno
N2O
28
16
N2O2
28
32
N2O3
28
48
N2O4
28
64
N2O5
28
80
3
Ipotetico esperimento per verificare l’inesattezza concettuale
della legge di Lavoisiere
La massa di un corpo è
una misura del suo
contenuto di energia
(Einstein).
In questo ipotetico
esperimento le due
batterie sono identiche
in ogni dettaglio se non
per il fatto che la
batteria di sinistra è
carica mentre l’altra è
scarica.
4
Modello atomico
Crisi della Fisica Classica
Problemi non risolti:
•
Stabilità della dimensione degli atomi
•
Emissione ed assorbimento da parte degli atomi di radiazioni
elettromagnetiche caratterizzate da frequenze discrete
•
Effetto fotoelettrico
•
Spettro delle frequenze emesse da un corpo riscaldato
5
Modello atomico - Sviluppo storico
Modelli Atomici
Spettri Atomici
Fisica Quantistica
Plank
Bunsen
Dalton
Atomi indivisibili
Thomson
Particelle subatomiche
Tubi di Crooke
Leggi di Faraday
Radioattività
Rutherford
Atomo nucleare
Spettri atomici
Rydberg
λ spettro H
Bohr
Onde stazionarie
Principio di
Indeterminazione di
Heisenberg
Radiazione corpo nero
Teoria dei quanti
Einstein
Fotoni
Effetto fotoelettrico
Orbite permesse
Postulato quantizzazione
De Broglie
Proprietà
corpuscolari - ondulatorie
dell’elettrone
Schrödinger
Numeri quantici
Stati energetici
Orbitali
Probabilità
6
Struttura atomica della materia
Teoria atomica di Dalton
La materia è costituita da atomi
indivisibili e indistruttibili
Tutti gli atomi di uno stesso elemento
hanno la stessa massa e le stesse
proprietà chimiche
Dalton
Atomi di elementi diversi hanno masse diverse e proprietà John
(1766 – 1844)
chimiche diverse
Gli atomi di elementi diversi si combinano fra loro in rapporti
di numeri interi
7
Modello atomico di Thomson
L’atomo è concepito come una sferetta con la massa e la carica positiva
uniformemente distribuita,con gli elettroni negativi in numero tale da rendere la
struttura complessivamente neutra.
Gli elettroni oscillano attorno a posizioni di equilibrio determinate dalle forze
di attrazione verso il baricentro delle cariche positive e le forze di repulsione
interelettroniche
Punti
negativi
elettroni
Nuvola positiva
8
Struttura atomica: modello atomico di Rutherford
Per interpretare i dati ottenuti inviando particelle α su sottilissime
lamine di oro, Rutherford propose un modello atomico che
prevedeva un nucleo estremamente piccolo attorno al quale
ruotavano uno o più elettroni su orbite molto ampie.
9
Modello atomico ( planetario ) di Rutherford
• Gli atomi sono costituiti da particelle
subatomiche,elettroni,protoni,e un ulteriore particella neutra(
ipotizzata ma non ancora individuata ).
• Il protone e la particella incognita formano un corpo centrale
compatto ( nucleo ) mentre gli elettroni ruotano attorno al
nucleo su orbite circolari o ellittiche ( nuvola elettronica )
10
Modello atomico di Rutherford
Atomi di
oro
Nucleo
dell’atomo
di oro
Particelle α
Il modello è incompatibile con le leggi della fisica classica in quanto
una particella carica che non si muove con moto rettilineo
uniforme,deve emettere energia sotto forma di radiazioni
elettromagnetiche
11
Modello atomico di Rutherford
elettroni
nucleo
Particella
sconosciuta
protone
Rutherford ipotizzò che all’interno del nucleo oltre ai protoni vi fosse
un secondo tipo di particella neutra (questa particella venne
successivamente chiamata neutrone e individuata sperimentalmente 12
nel 1932)
Spettro di emissione del corpo nero
Emissione del
corpo nero
Risultati sperimentali
Previsione “classica”
La “catastrofe
ultravioletta”
13
Lo spettro del corpo nero
emissione secondo le leggi classiche
curve sperimentali
Secondo le leggi classiche dell’elettromagnetismo l’emissione è
dovuta agli oscillatori elettronici elementari che oscillano con
tutte le frequenze emettendo una radiazione corrispondente, di
intensità:
2 κT
I =
c2
2
κ = costante di Boltzmann
Incongruenza con i dati sperimentali
14
Teoria dei Quanti
Planck postulò che ogni oscillatore elementare (gli
elettroni all’interno dell’atomo) potesse assorbire o emettere
solo quantità di energia che fossero multipli interi di una
quantità minima finita, ε , caratteristica di ogni oscillatore; in
altre parole l’energia poteva essere assorbita o emessa solo per
salti successivi di grandezza ε (quantità discrete o quanti).
ε
= h• ν
h = costante di Planck (6.625 •10-27erg • s)
ν = frequenza dell’oscillatore
15
Effetto fotoelettrico
Emissione di elettroni da parte
di una superfice metallica (ad
esempio potassio o sodio) colpita
da una radiazione elettromagnetica
di opportuna frequenza
Osservazioni sperimentali
• Per ogni metallo esiste una frequenza minima (ν
ν0 : frequenza di soglia)
tale che l’effetto si osserva solo per radiazioni aventi ν maggiore di ν0
• L’energia cinetica massima degli elettroni emessi è indipendente
dall’intensità della radiazione incidente, ma dipende da ν
• Fissata la frequenza, il numero di elettroni emessi è proporzionale
all’intensità della radiazione incidente
16
Interpretazione di Einstein
Una radiazione elettromagnetica è costituita da pacchetti elementari
(chiamati quanti di luce e successivamente fotoni) ognuno dei quali
trasporta quantità di energia pari a E = h ν ; quando un fotone
colpisce un atomo gli trasferisce la sua energia e se questa è
maggiore dell’energia E0 necessaria per strappare l’elettrone meno
legato si verifica l’espulsione.
Quindi si osserva l’effetto fotoelettrico quando:
h ⋅ν ≥ E0
La frequenza di soglia viene definita dalla
relazione:
ν ≥ E0 / h
ν 0 = E0 / h
17
Emax = h ν - h ν0
energia E0
energia fotone incidente
da cui:
Legge di Einstein
Emax = h ( ν − ν0 )
Emax
Andamento di Emax
in funzione di ν
ν0
ν
18
Energia cinetica massima dei fotoelettroni emessi
da alcuni metalli
Ecin = Efot-Eemis = hν – hν0
Ecin = h ( ν – ν0 )
Na
Li
pendenza = h = 6.6260755 10 -34 19
J sec
Massa e quantità di moto di un quanto di luce
Sappiamo che: E = m c2
eguagliando otteniamo:
e per la luce:
mν c2 = h ν
mν =
quindi:
E= hν
h ν / c2
massa di un quanto
calcoliamo la quantità di moto:
pν = mν c = (h ν / c2) c = h ν / c
e dato che:
λ = c/ ν
pν = h / λ
λ = h / pν
quantità di moto di un quanto
20
Compton
(1922)
21
22
L’immagine della coppa è formata da 2 profili facciali di fronte
23
Spettri atomici:interazioni delle radiazioni
elettromagnetiche con i sistemi atomici e
molecolari
Verso la metà del 1800 Bunsen iniziò degli studi riguardanti le interazioni
delle onde elettromagnetiche con la materia; tali studi vennero
successivamente ampliati e razionalizzati ad opera di Balmer, Paschen,
Rydberg, etc.
I dati sperimentali ottenuti vennero elaborati ottenendo relazioni empiriche
che permettevano di descrivere le osservazioni fatte. Tuttavia, non avendo
a disposizione un modello atomico accettabile risultava impossibile fornire
una interpretazione teorica di questi dati.
24
Generalità sulle onde elettromagnetiche
λ
Emax
Ampiezza massima: Emax (Bmax)
Lunghezza d’onda: λ (nm, Å)
Periodo: τ (s)
Frequenza:
=
1
λ ⋅ν = c
=c =
(s-1)
Numero d’onda: ~ = 1 (cm-1)
~=1=
c
c
25
Spettri di emissione e di assorbimento degli atomi
Quando un corpo viene riscaldato, ad esempio il filamento di una
lampadina, emette radiazioni elettromagnetiche. Se queste
radiazioni vengono inviate su di un prisma, questo le separa in
funzione delle loro lunghezze d’onda (avendo angoli di
diffrazione diversi).
Se le radiazioni così separate vengono inviate su una lastra
fotografica, si ottiene uno spettro continuo, cioè tutte le zone della
lastra, corrispondenti ognuna ad una specifica lunghezza d’onda,
vengono interessate.
Al contrario se eccitiamo dei singoli atomi, ad esempio con un
arco elettrico, ed andiamo ad analizzare le radiazioni emesse,
otteniamo degli spettri a righe (chiamati anche spettri atomici).
26
Spettro di emissione dell’atomo di idrogeno
Spettro a righe
Prisma
Lastra
fotografica
Campione
Fenditura
27
Spettro di emissione dell’atomo di idrogeno
Serie di
Balmer
Serie di
Lyman
Lunghezza d’onda (nm)
Infrarossi
Visibile
Ultravioletto
n=
Serie di Balmer
ν =R
H
1
1
−
2 2 n2
RH = 109677.76 cm-1
28
Spettro di emissione dell’atomo di idrogeno
Serie di
Balmer
Serie di
Lyman
Lunghezza d’onda (nm)
Infrarossi
Visibile
Equazione di Ridberg
1
1
ν = RH
−
2
m n2
m = 1, 2, 3, …,
Ultravioletto
Serie
Lyman
Balmer2
Paschen
Brackett
Pfund
m
n
1
2, 3, 4, ...
3, 4, 5, ...
3
4, 5, 6, ...
4
5, 6, 7, ...
5
6, 7, 8, ...
n = m + 1, …,
Valida anche per ioni idrogenoidi (He+, Li++, Be+++, …)
29
Modello atomico di Bohr
Modifica il modello di Rutherford introducendo due postulati
r
Leggi della fisica classica applicate all’atomo di
idrogeno; tra elettrone e nucleo vi è attrazione
coulombiana, definita dalla relazione:
2
e
F= 2
r
e = carica dell’elettrone
r = raggio dell’orbita
tale forza di interazione deve rispettare anche la relazione:
F = m⋅a
m = massa dell’elettrone
a = accel. centripeta
30
dato che:
acen
v2
=
r
si ha:
v2
F = m⋅
r
v2
e2
= m⋅
2
r
r
quindi:
esplicitando r e ν otteniamo le espressioni:
2
e
r=
2
m⋅v
e
ν=
m⋅r
In base a queste relazioni, il raggio dell’orbita è funzione soltanto
della velocità e quindi, non essendovi limitazioni per questa, anche il
raggio può assumere qualsiasi valore.
31
Analogamente anche per l’energia totale dell’elettrone non vi sono limitazioni,
infatti:
E = E cin
2
1
e
2
+ E p = mv −
2
r
dalla relazione esprimente r otteniamo:
2
e
mv =
r
2
quindi:
1 e2 e 2
1 e2
E=
−
=−
2 r
r
2 r
32
Primo postulato di Bohr
Il valore del momento della quantità di moto dell’elettrone ruotante
attorno al nucleo deve essere un multiplo intero della quantità h/2π
+
r
-
v
h
mvr = n
2π
con n = 1, 2, 3, . . . .
Questa limitazione, come conseguenza, porta alla quantizzazione del raggio
delle orbite e dell’energia totale dell’elettrone; dall’equazione sopra scritta
otteniamo:
h
v=n
2π rm
mentre dalla relazione che ci definisce r otteniamo per la ν la seguente
espressione:
e
v=
mr
33
Eguagliando le due espressioni si ottiene:
elevando al quadrato:
per cui:
h
n
=
2π rm
e
mr
2
2
e
h
n2 2 2 2 =
4π r m
mr
2
h
2
rn = n
2
2
4π me
Quindi il raggio dell’orbita risulta definito da n (numero quantico).
34
introducendo i valori numerici delle costanti (h, e, m, π) nella
espressione di rn si ottiene:
−8
rn = n 0,529 ⋅10 (cm)
2
per
n=1
r1= 0,529 (A)
per
n=2
r2 = 22 0,529 = 2,116 (A)
r1= 0,529 A viene chiamato primo raggio di Bohr e viene usato
come unità di misura della lunghezza per dimensioni
atomiche.
35
Quantizzazione dell’energia
Sappiamo che:
2
2
2
1e e
1e
E=
− =−
2r r
2r
Introducendo nella relazione che ci
permette di calcolare E l’espressione di
rn otteniamo:
2
h
2
rn = n
4 π 2 me 2
1 2π me
En = − 2
2
n
h
2
4
Quindi anche i valori che l’energia dell’elettrone può assumere
dipendono unicamente da n.
Sostituendo nella espressione di E i valori delle costanti si ottiene:
per n = 1
E1= -13,6 eV
per n = 2
E2= -3,4 eV
1
En = − 2 13,6 (eV )
n
36
Secondo postulato di Bohr
L’atomo emette o assorbe energia sotto forma di radiazioni
elettromagnetiche solo quando si hanno delle transizioni, cioè dei
passaggi tra stati quantici diversi e quando ciò si verifica l’energia
corrispondenti alla differenza tra i livelli energetici propri degli stati
quantici tra i quali avviene la transizione è emessa o assorbita sotto
forma di un singolo fotone
∆E = En - En’
energia del livello di numero quantico n’
energia del livello di numero quantico n
questa energia viene
scambiata sotto forma
di un singolo fotone
∆E = h ν
E n − E n'
ν =
h
En - En’ = h ν
Legge di Bohr
37
Il modello atomico di Bohr: secondo postulato
Energia
Energia
EA > EB
νA > νB
λA < λB
Transizione
Frequenza
Spettro
Emissione
38
Teoria di Bohr dell’atomo di idrogeno
Grandezze relative
delle prime cinque orbite
di Bohr per l’atomo di idrogeno
39
Energia di ionizzazione dell’atomo di idrogeno
Calcolo dell’energia di ionizzazione dell’atomo di idrogeno:
Energia del livello avente n = ∞
EI = E∞ − E1
Sappiamo che:
Energia del livello avente n = 1
1 2π 2 me 4
En = − 2
n
n2
Usando i valori delle varie costanti si ottiene:
1
E n = − 2 ⋅ 13,6 (eV)
n
per n = ∞
E∞ = 0
per n = 1
E1 = −13,6 eV
EI = 0 − ( − 13, 6 ) = 13, 6 eV
40
Modelli molecolari di Bohr per H2, O2, H2O (1912).
Riprodotti da disegni di Bohr (Memorandum, estate 1912).
41












