Liceo L.daVinci – 12/02/2013 - simulazione di 2° prova
SOLUZIONE - QUESITI da 1 a 4
prof.ssa Di Vito
QUESITI
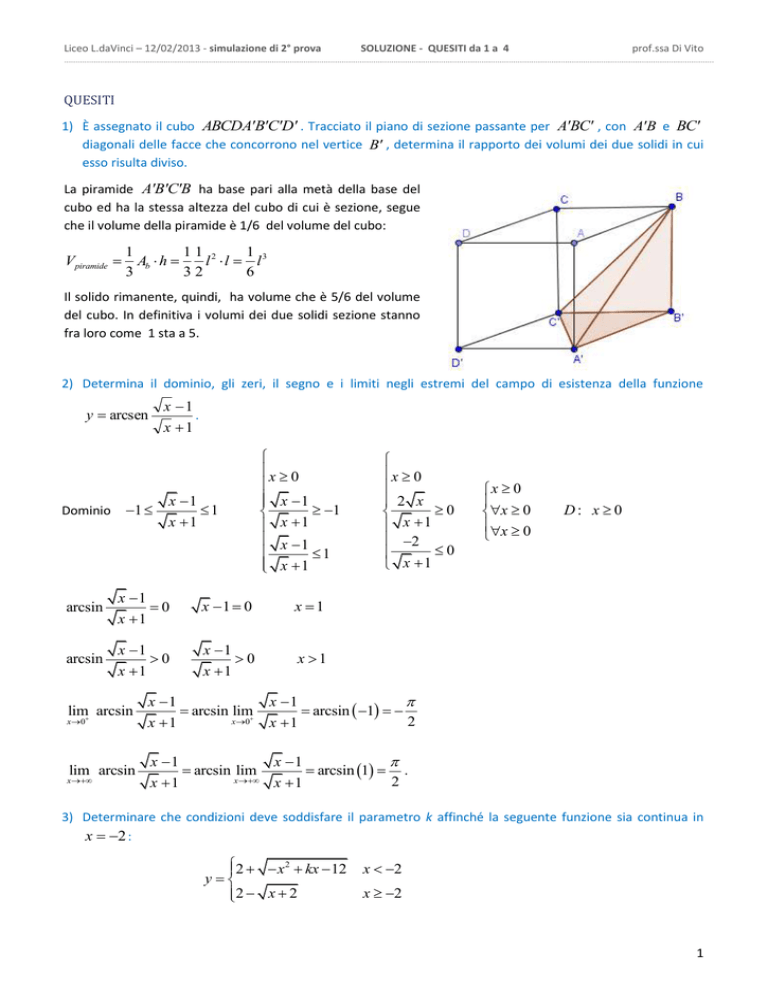
1) È assegnato il cubo ABCDA'B'C'D' . Tracciato il piano di sezione passante per A'BC' , con A'B e BC'
diagonali delle facce che concorrono nel vertice B' , determina il rapporto dei volumi dei due solidi in cui
esso risulta diviso.
La piramide A'B'C'B ha base pari alla metà della base del
cubo ed ha la stessa altezza del cubo di cui è sezione, segue
che il volume della piramide è 1/6 del volume del cubo:
Vpiramide
1
11 2
1
Ab h
l l l3
3
32
6
Il solido rimanente, quindi, ha volume che è 5/6 del volume
del cubo. In definitiva i volumi dei due solidi sezione stanno
fra loro come 1 sta a 5.
2) Determina il dominio, gli zeri, il segno e i limiti negli estremi del campo di esistenza della funzione
x 1
y arcsen
Dominio
x 1
1
.
x 1
1
x 1
x 0
x 1
1
x
1
x 1
1
x 1
arcsin
x 1
0
x 1
x 1 0
x 1
arcsin
x 1
0
x 1
x 1
0
x 1
x 1
x 0
2 x
0
x
1
2
0
x 1
x 1
arcsin lim
x 0
x 1
lim arcsin
x 1
x 1
arcsin lim
arcsin 1 .
x
2
x 1
x 1
x
D: x 0
x 1
arcsin 1
2
x 1
lim arcsin
x 0
x 0
x 0
x 0
3) Determinare che condizioni deve soddisfare il parametro k affinché la seguente funzione sia continua in
x 2 :
2
2 x kx 12
y
2 x 2
x 2
x 2
1
Liceo L.daVinci – 12/02/2013 - simulazione di 2° prova
SOLUZIONE - QUESITI da 1 a 4
prof.ssa Di Vito
Determinare il dominio della funzione trovata e stabilire se è derivabile in ogni suo punto.
lim
x 2
lim
x 2
2
x 2 kx 12 2 16 2k
2 x 2 f (2) 2
2
2 x 8 x 12
y
2 x 2
2 16 2k 2
k 8
x 2
x 2
Dominio:
per la prima funzione, per x 2 bisogna imporre x2 8x 12 0
x 2
per la seconda funzione si ha
quindi risulta
D:
quindi 6 x 2
6;
2 x 8
2 x 2 8 x 12
f '( x)
1
2 x 2
x 2
D ':
6; 2 2;
x 2
La funzione non è derivabile in x=-6 e x=-2, che sono punti a tangente verticale
lim
x 6
lim
x 2
x 4
x 8 x 12
2
x 4
x 8 x 12
2
2
0
2
0
1
1
lim
0 .
2 x2
x 2
4) Traduci la seguente scrittura utilizzando il linguaggio dei limiti
M 0, 0 : x con 2 x 2 ,
3
M.
2x 4
Esegui la verifica del limite, rappresenta il grafico della funzione evidenziando il limite precedente, e
rappresenta graficamente y f x .
La scrittura insiemistica significa:
lim
x 2
3
.
2x 4
Verifica del limite:
3
M
2x 4
3 M (2 x 4)
0
2x 4
2
Liceo L.daVinci – 12/02/2013 - simulazione di 2° prova
N 0
D0
SOLUZIONE - QUESITI da 1 a 4
3 M (2 x 4) 0
2x 4 0
x 2
x 2
3
2M
prof.ssa Di Vito
-2
-2+3/(2M))
N
+
+
-
D
-
+
+
N/D -
+
-
È l’intorno destro di -2, il limite è verificato.
3
è una funzione omografica di centro C (2;0) . Non ha intersezioni con gli assi,
2x 4
calcolo le coordinate di due o tre punti: A(1;1/ 2) B(1;3 / 2) C (4;1/ 4) e i loro simmetrici rispetto a C
La funzione y
3
2 x 4
y f ( x)
3
2 x 4
per x 2
il grafico si ottiene per simmetria rispetto all’asse x per le x<-2.
per x 2
3











