ESERCIZI E TEST FUNZIONE ESP E LOG

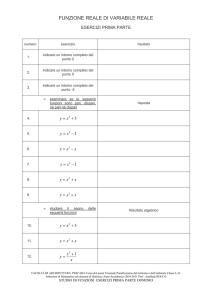
ESERCIZI E TEST FUNZIONE ESPONENZIALE E LOGARITMICA
1. Calcolare il valore delle seguenti potenze:
1
 
 3
3−2
−2
 3
 
5
−2
1
 
2
2 −1
0
1
 
5
−1
1
 
 3
−4
2. Trasformare le seguenti potenze in radicali :
3
2
1
4
1
 
2
 33
 
 5
−
1
2
(5)− 2
3
3. Trasformare i seguenti radicali in potenze ad esponente razionale:
3
3
5
5
5
1
3
5
1
 
 3
2
4. Date le seguenti funzioni esponenziali calcolare in tabella alcuni valori ( almeno 5 ) , tracciare il grafico
per punti e studiare il comportamento asintotico per x → +∞ e x → −∞
y=2
1
y= 
 4
−x
y=3
x
−x
1
y= 
 2
x
5. Date le seguenti funzioni logaritmiche calcolare in tabella alcuni valori ( almeno 5 ) , tracciare il grafico
per punti e studiare il comportamento asintotico per
y = log 2 x
y = log 1 x
y = log 3 x
x → 0+
2
6. Rispondere ai seguenti quesiti:
a. Il logaritmo log 4 16 è uguale a :
a.
b.
c.
d.
e.
b. Il logaritmo
a.
b.
c.
d.
e.
c.
Il logaritmo
4;
2;
0;
non esiste;
nessuna delle precedenti.
log −3 9 è uguale a :
-2;
2;
0;
non esiste;
nessuna delle precedenti.
log 3 5 è uguale a :
a. 2;
b. 5;
c.
d.
log 5 10
;
log 3 10
log10 5
;
log10 3
e. nessuna delle precedenti.
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 1 di 3
d. Il logaritmo
a.
b.
c.
d.
e.
e. Se
0;
5;
1;
non esiste;
nessuna delle precedenti.
log 5 x = 0 allora :
a.
b.
c.
d.
e.
f.
log 5 1 è uguale a :
x = 0;
x = 1;
x = 5;
il logaritmo non si può calcolare;
nessuna delle precedenti.
Il logaritmo
log 2 53 si trasforma in :
a.
3 ⋅ log 2 5 ;
b.
15 ⋅ log 2 5 ;
c.
125 ⋅ log 2 5 ;
d.
2 log10 53 ;
e. nessuna delle precedenti.
x
1
g. La funzione esponenziale y =   pere x → +∞ tende a :
 5
a. 0;
b. +∞ ;
c. −∞ ;
d.
1
;
5
e. nessuna delle precedenti.
x
1
h. La funzione esponenziale y =   per x → −∞ tende a :
 5
a. 0;
b. +∞ ;
c. −∞ ;
d. 5 ;
e. nessuna delle precedenti.
i.
La funzione esponenziale y = (5)
a. 0;
b. +∞ ;
c. −∞ ;
d. 5 ;
e. nessuna delle precedenti.
−x
x → −∞ tende a :
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 2 di 3
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
Pagina 3 di 3