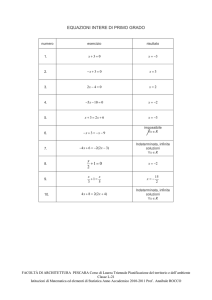
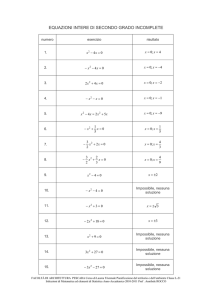
FUNZIONE REALE DI VARIABILE REALE
ESERCIZI PRIMA PARTE
esercizio
numero
risultato
1.
Indicare un intorno completo del
punto 2
2.
Indicare un intorno completo del
punto 0
3.
Indicare un intorno completo del
punto -5
•
esaminare se le seguenti
funzioni sono pari, dispari,
né pari né dispari
4.
y = x2 + 3
5.
y = x2 − 1
6.
y = x3 − x
7.
y = x3 − 1
8.
y = x2 + x
9.
y = x3 + x
•
studiare il segno
seguenti funzioni
10.
y = x2 + 3
11.
y = x2 + x
12.
x2 + 1
y=
x
delle
risposta
Risultato algebrico
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
STUDIO DI FUNZIONI ESERCIZI PRIMA PARTE DOMINIO
x2 − 1
x
13.
y=
14.
y = 2( x − 2 )
15.
y = ( x − 1) ⋅ 2( x − 2 )
16.
y = log 2 ( x + 5)
17.
y = log 2 ( x − 5)
18.
y = log 1 ( x + 3)
2
y = log 1 ( x + 2)
19.
2
y = log 2 (3x 2 − 2 x )
20.
•
21.
22.
dopo aver individuato il tipo
di funzione determinare il
dominio
delle
seguenti
funzioni :
tipo di funzione
Dominio algebrico
y = x2 + 2x + 5
y=
x2 − 1
x2 − 4
23.
y=
x+5
x − 4x + 3
24.
y=
x+5
x − 4x + 5
25.
y = x2 + x + 1
26.
y = − x 2 + 3x
27.
y = x2 − 1 + 9 − x2
2
2
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
STUDIO DI FUNZIONI ESERCIZI PRIMA PARTE DOMINIO
28.
y = x − 3 + 1− x
29.
y=
x+3
x−4
30.
y=
x2 + 3
x−4
31.
y=
x+3
x−4
32.
y=
x+3
x−4
33.
y = log10 ( x − 3)
34.
y = log10 ( x 2 − 3 x )
35.
y = log10 ( x 2 − 3 x + 2)
36.
y = log10 ( x 2 − 3x + 5)
37.
y = log10 (1 − 3x )
38.
y = log 1 (6 + 3x )
2
x −1
39.
y = 3 x−3
40.
y = 3 x −3
x −1
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
STUDIO DI FUNZIONI ESERCIZI PRIMA PARTE DOMINIO
•
scrivere a piacere una
funzione
che
abbia
il
seguente dominio :
41.
D = {∀x ∈ R / x ≠ 3}
42.
D = {∀x ∈ R / x ≥ 2}
y = x−2
43.
D = {∀x ∈ R / 0 ≤ x ≤ 2}
y = − x2 + 2x
44.
D = {∀x ∈ R / 0 < x < 2}
y=
45.
D = {∀x ∈ R / x ≥ 2}
46.
D = {∀ x ∈ R / x ≠ 0 ∧ x ≠ 2 }
y=
1
x−3
1
− x 2 + 2x
y = x−2
y=
1
x − 2x
2
FACOLTÀ DI ARCHITETTURA PESCARA Corso di Laurea Triennale Pianificazione del territorio e dell’ambiente Classe L-21
Istituzioni di Matematica ed elementi di Statistica Anno Accademico 2010-2011 Prof . Annibale ROCCO
STUDIO DI FUNZIONI ESERCIZI PRIMA PARTE DOMINIO