Sesta Esperienza: Determinazione della costante di Boltzmann

Dipartimento di Matematica & Fisica - Corso di Laurea in Fisica - Esperimentazioni di Fisica III
Prof. Giuseppe Schirripa Spagnolo
Sesta Esperienza: Determinazione della costante di
Boltzmann tramite caratteristica del BJT
Eseguita in data ………………………….
STUDENTE:……………………………………………………………………………………………………………………………………………
.
STUDENTE: …………………………………………………………………………………………………………………………………………..
1
Per l’esperienza si utilizzeranno:
 BJT 2N3904
 Diodo 1N4148
 Resistenze da: 10 kΩ, 7.5 kΩ, 1 kΩ (variabile)
 Condensatore 22 µF
 Amplificatore operazionale TL081
 Alimentatore duale
 breadboard
2
Premessa
Secondo il modello di Modello di trasporto completo del BJT (si veda Figura) le equazioni delle
correnti che scorrono nel transistor npn, sono:

 v
iC  I S exp  BE
 BEVT

 vBC   I S 
 vBC

exp 
 
  exp 

 BCVT    R 
 BCVT
 
  1 ;
 

 v
 I 
 v

 v
 
iE  I S exp  BE   exp  BC    S exp  BE   1 ;
 BEVT 
 BEVT  
 BCVT    F 

iB 
 vBE
IS 
exp 
 F   BEVT
  IS
  1 
  R

 vBC
exp 
  BCVT

 
  1 .
 
Ipotizziamo di polarizzare il BJT con vBE   4kBT  q  0.1 V e vBC   4kBT  q  0.1 V
Con queste polarizzazioni, per un transistor npn, valgono le approssimazioni:

 v
iC  I S exp  BE

 BEVT
 vBC

  exp 

 BCVT

 v
 v

iE  I S exp  BE   exp  BC

 BEVT 
 BCVT
iB 
 vBE
IS 
exp 
 F   BEVT
  IS

   R

 v
 
 exp  BC   1 ;

 BCVT  
  IS 
 vBE  
exp 

  1 ;
 BEVT  
   F 
 vBC  
  IS 

1

exp


  1 .
 
   R 
 BCVT  
Quindi:
 v
iC  I S exp  BE
 BEVT
 IS
.

 R
Se si sceglie di utilizzare un BJT con IS piccola e R non troppo piccolo (generalmente un “normale”
transistor rispetta queste ipotesi) si può trascurare il termine IS/R.
Nella nostra esperienza utilizzeremo un 2N3904; questo transistor ha BE  1.004. Pertanto, se
questo BJT viene polarizzato con vBE > 0.5 V, abbiamo:
3
v 
iC  I S exp  BE  .
 VT 
Ricordando che VT 
k BT
ed effettuato il logaritmo naturale di entrambi i membri, otteniamo:
e
v 
e
iC  I S exp  BE   ln(iC ) 
 vBE  ln  I S  .
k BT
 VT 
In altre parole, abbiamo una funzione lineare che lega il logaritmo naturale della corrente di
emettitore con la differenza di potenziale presente tra la base e l’emettitore del transistor.
Pertanto, effettuando un fit lineare, si ottiene una retta che ha pendenza VT e intercetta IS.
Conoscendo la temperatura della giunzione (se nel transistor si fa scorrere una “piccola” iC, la
temperatura della giunzione si può approssimare con quell’ambiente) e la carica dell’elettrone, si può
fare una stima della costante di Boltzmann.
Esperienza di Laboratorio
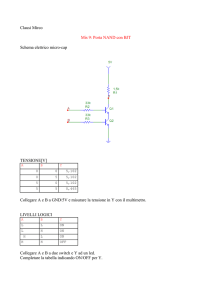
Per la determinazione della costante di Boltzmann si utilizza il seguente circuito:
Il circuito, di per se molto semplice:
 BJT polarizzato tramite una resistenza variabile e la massa virtuale di un amplificatore
operazionale;
 amplificatore operazionale è montato in configurazione “convertitore correntetensione”.
Un alimentatore duale fornisce l’alimentazione all’amplificatore operazionale e tramite una
resistenza variabile, polarizza il BJT.
4
Il circuito montato su breadboard risulta:
Resistenza variabile da 1 kΩ
L’amplificatore operazionale “legge” la corrente di collettore del BJT, praticamente, senza
influenzarla.
L’amplificatore operazionale trasforma la corrente di collettore del BJT in tensione:
Vout  iC  RF (nel nostro caso la RF = 10 kΩ  1 kΩ - ovviamente la resistenza si può misurare con
maggiore precisione); nella nostra configurazione si ottiene una tensione d’uscita positiva in quanto la
corrente che scorre nella resistenza di feedback dell’amplificatore operazionale a verso che va dall’uscita
al BJT (conseguenza della tensione negativa posta sull’emettitore del BJT)
Un multimetro in grado di leggere frazioni di millivolt è utilizzato per leggere la VBE presente tra la
base e l’emettitore del transistor. (multimetro Agilent).
Invece, per leggere la tensione d’uscita dell’amplificatore operazionale è sufficiente un voltmetro in
grado di leggere i millivolt. (multimetro portatile Fluke).
Attraverso la resistenza variabile da 1 kΩ si cambia la vBE del transistor.
Per cambiare il valore della resistenza variabile si agisce con un piccolo cacciavite sulla vite presente
sul componente. Al fine di evitare problemi sui contatti, quando si ruota la vite della resistenza variabile,
con un dito si spinge la resistenza contro la breadboard.
5
Variando il valore della vBE, si ricava la seguente tabella:
vBE [V]
vout [V]
iC = vout/10 kΩ
ln (iC)
0.5
1
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
6.5
7
7.5
8
8.5
9
9.5
10
6
Effettuando un fit lineare tra ln(iC) vs. vBE è possibile ricavare ln(IS) (intercetta della retta) e VT.
Conseguentemente si può fare una stima della costante di Boltzmann.
Effettuata questa prima parte dell’esperienza, si sostituisce il BJT con il diodo 1N4148.
Pertanto il circuito diventa:
In questo caso abbiamo:

 v
iD  I S exp  D
 VT

 
  1
 
Nella nostra esperienza utilizzeremo un 1N4148; questo transistor ha   1.9. Pertanto, se questo
Diodo viene polarizzato con vD > 0.5 V, abbiamo:
 v 
e
iD  I S exp  D   ln(iD ) 
 v  ln  I S  .
 k BT D
 VT 
7
Pertanto, effettuando un fit lineare, si ottiene una retta che ha pendenza VT e intercetta IS.
Conoscendo la temperatura della giunzione (se nel Diodo si fa scorrere una “piccola” iD, la
temperatura della giunzione si può approssimare con quell’ambiente) e la carica dell’elettrone, si può
fare una stima della costante di Boltzmann moltiplicata per .
Carica dell’elettrone: e  1.6010-19 C
Costante di Boltzmann kB  1.3810-23 JK-1
8