Misure di potenza I wattmetri di laboratorio hanno solitamente la

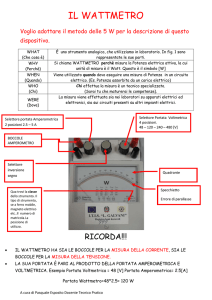
Misure di potenza
I wattmetri di laboratorio hanno solitamente la bobina amperometrica realizzata con poche
spire di sezione relativamente elevata, suddivisa in due sezioni uguali che possono essere
messe in serie o parallelo (due portate amperometriche). La bobina voltmetrica è invece
costituita da molte spire di piccola sezione, associate alla quale sono più resistenze addizionali
(più portate voltmetriche). In realtà la misura effettuata con il wattmetro è affetta da errore
sistematico la cui entità dipende dall’autoconsumo dello strumento e il cui segno è sempre
positivo (si misura sempre in più). Questo vale nel caso in cui la voltmetrica sia derivata
sia a valle sia a monte. Si ricorda infatti che nel primo caso si ha:
PM
VU2
= PU +
RV
(1)
e nel secondo caso
PM = PU + IU2 RA
(2)
Si noti che a differenza della bobina voltmetrica, quella amperometrica è di rame per cui va
a dipendere dalla temperatura. Il wattmetro è anche affetto da un altro errore sistematico
attribuibile allo sfasamento tra la tensione applicata alla voltmetrica e la corrente che attraversa la bobina stessa. Poiché è di difficile valutazione, di esso si tiene implicitamente conto
nella classe che caratterizza lo strumento.
In un circuito sinusoidale un wattmetro elettrodinamico ha la bobina fissa percorsa dalla
corrente I˙f = I˙ e la bobina mobile percorsa dalla corrente I˙m . In prima approssimazione la
corrente circolante nella bobina mobile può essere assunta come:
V̇
I˙ =
RV
(3)
In quest caso l’angolo β tra I˙f e I˙m coincide con l’angolo φ tra V̇ e I˙ per cui l’espressione
della coppia media vale:
c = kIf Im cosβ =
k
V Icosφ = k ′ P
RV
(4)
Lo strumento misura quindi la potenza P con costante k ′ valida sia in c.c. sia in c.a. anche
per grandezza non sinusoidali fino alle frequenze per cui vale la relazione (3).
1
L’ipotesi (3) trascura l’angolo ǫ esistente I˙m e V̇ (per convenzione si assume ǫ positivo
se I˙m precede V̇ ). La convenzione fa riferimento a quanto anche detto per i trasduttori in
riferimento all’errore d’angolo. In particolare, l’errore d’angolo, ossia la differenza di fase fra
la grandezza d’uscita e la grandezza di ingresso è considerato positivo quando la grandezza
d’uscita precede quella d’ingresso. La presenza di ǫ equivale a un errore sull’angolo φ per
cui:
dP =
d
(V Icosφ)ǫ = −ǫV Isinφ
dφ
(5)
e quindi esprimendo l’errore relativo
dP
= −ǫtanφ
P
(6)
Non potendo annullare l’induttanza della bobina, si procede al suo rifasamento mediante
l’inserzione di un condensatore in parallelo a parte del resistore voltmetrico (per ottenere un
rifasamento valido per la banda di frequenze d’impiego). Nel caso in cui ǫ sia dovuto solo
alla presenza della reattanza della bobina mobile vale
ǫ=−
ωLm
RV
(7)
Un wattmetro con valori nominali V0 , I0 , cosφ0 va in fondo scala per la potenza P0 =
V0 I0 cosφ0 . Poiché raramente i tre valori nominali si presentano contemporaneamente, specie
se cosφ0 = 1, la maggior parte degli strumenti ammette sovraccarichi di tensione e di corrente
fino a valori VM , IM specificati dal costruttore. I wattmetri per basso cosφ mantengono
un’alta sovraccaricabilità e un piccolo errore di fase, uniti a un ridotto consumo, il tutto al
fine di facilitare le misure su carichi a basso cosφ. Poiché il fattore di potenza deve essere
considerato come una grandezza d’influenza, le variazioni che si ammettono a tensione e
corrente nominali, quando questa grandezza varia nel suo campo d’impiego (ossia fra cosφ0
e zero) devono essere minori dell’indice di classe. Deve perció essere:
dP ≤ ǫV0 I0 < CP0 /100
(8)
da cui si deriva (per ǫ in centiradianti):
ǫ < Ccosφ0
2
(9)
Misura di potenza su circuiti in c.a. monofase
Ogni sezione di misura in un circuito monofase in regime di c.a. è caratterizzata da tre valori:
tensione fra i conduttori, corrente attraverso di essi, sfasamento tra queste due grandezze.
Un metodo per individuare queste tre grandezze è l’ultilizzo di tre strumenti, che sono
usualmente un amperometro, un voltmetro e un wattmetro. Dalle loro letture deriva I, V e
P da cui poi si può ricavare:
Q=
q
(V I)2 − P 2
(10)
P
VI
(11)
cosφ =
Z=
V
I
(12)
Rimane però indeterminato dalle relazioni precedenti il segno da attribuire alla potenza
reattiva. Per questo si può procedere in vari modi: inserendo un condensatore in parallelo
al carico, variando la frequenza di alimentazione, disponendo in serie al circuito voltmetrico
del wattmetro una reattanza magnetica X in modo da introdurre un errore di fase. In
particolare, in quest’ultimo caso, l’indicazione del wattmetro aumenta se il carico è induttivo,
diminuisce se capacitivo.
Per risolvere il problema della determinazione dell’errore strumentale conviene utilizzare
relazione algebriche tra le potenze che sussistono grazie al teorema di Boucherot. Con
l’ipotesi di voltmetrica derivata a valle si ha:
V = Vz
(13)
e per la conservazione delle potenze attive entranti nel nodo circuito di alimentazione, voltmetrica e carico
P = Pz +
V2
Re
(14)
dove Re rappresenta il parallelo tra la resistenza del wattmetro (circuito voltmetrico) e la
resistenza del voltmetro. Per la conservazione delle potenze reattive vale:
3
Q2 = (V I)2 − P 2 = Q2z = (Vz Iz )2 − Pz2
(15)
da cui si ottiene combinando le relazioni
Iz2 = I 2 −
P + Pz
Re
(16)
Questa correzione è sempre minore o al più uguale alla correzione algebrica:
Iv =
V
Re
(17)
In prima approssimazione, infatti, si ha:
P + Pz ≈ 2P = 2V Icosφ
(18)
da cui per la (16) si ha:
I − Iz
≈
eI ≈
I
s
1−
Iv
2V
cosφ ≈ cosφ
Re I
I
(19)
relazione che può essere comoda per un calcolo preliminare approssimato dell’errore.
Nel caso le bobine amperometriche siano a valle esse presentano una resistenza complessiva Ra e una reattanza complessiva Xa da cui:
P = Pz + Ra I 2 ; Q = Qz + Xa I 2 ; Vz2 =
Pz2 + Q2z
I2
(20)
Un wattmetro presenta due coppie di morsetti, l’una amperometrica (generalmente di maggiori dimensioni) da collegare in serie al circuito su cui si esegue la misura, l’altra, voltmetrica, da collegare in derivazione. Occorre però saper scegliere la connessione corretta in base
alle seguenti considerazioni:
a) la coppia motrice direttamente proporzionale alla potenza, cambia segno se si invertono
le connessioni amperometriche o quelle voltmetriche;
b) nei wattmetri elettrodinamici è opportuno che la bobina mobile sia praticamente allo
stesso potenziale della bobina fissa per evitare effetti elettrostatici tra le bobine (coppie
elettrostatiche, correnti capacitive) e, al limite, scariche elettrostatiche;
c) il wattmetro è sempre affetto da errore di consumo, per cui la connessione voltmetrica
va inserita a monte o a valle a seconda dello schema scelto per la misura.
4
Detta C la classe del wattmetro e V0 , I0 , cosφ0 i suoi valori nominali, si ha una fascia
d’incertezza d’ ampiezza percentuale del tipo:
η% =
C0
CV0 I0 cosφ0
=
P
V Icosφ
(21)
A questo errore si può in parte ovviare scegliendo un wattmetro con portate massime VM ≥
V > V0 e IM ≥ I > I0 , quindi sovraccaricando lo strumento entro i limiti consentiti o
scegliendo un wattmetro per basso cosφ, ossi con cosφ0 < 1.
Nel caso si voglia eseguire una misura escludendo l’uso di wattmetri si ricorre al metodo
dei tre voltmetri o al suo duale dei tre amperometri.
In entrambi i casi si ricorre a
un’impedenza di modulo Z0 e argomento γ. La corrente è definita da I = V2 /Z0, mentre la tensione da V = V3 . Si trascurano gli errori strumentali e dal teorema di Carnot si
ricava:
V12 = V32 + V22 + 2V2 V3 cosβ
(22)
essendo poi φ = γ − β la misura è stata completata. Per limitare l’influenza degli errori strumentali l’impedenza Z0 deve essere dello stesso ordine di grandezza dell’impedenza incognita
Z; ciò conduce spesso ad adottare per Z0 reattanze capacitive, in cui non si ha praticamente
dissipazione di energia. La potenza dissipata su un carico L può essere misurata utilizzando
un resistore R e per cui γ = 0. Le relazioni in termini di grandezze istantanee valgono:
1 ZT
1ZT
v3 idt =
v3 v2 dt
P =
T 0
T R0 0
(23)
v12 = (v2 + v3 )2 = v22 + v32 + 2v2 v3
(24)
e ancora:
da cui risulta
P =
1 ZT 2
1
(v1 − v22 − v32 )dt =
(V12 − V22 − V32 )
2T R0 0
2R0
(25)
che permette il calcolo della potenza attraverso l’uso dei valori efficaci letti dai tre voltmetri.
Gli errori assoluti propri dei tre voltmetri EV i = Ci Voi /100 dove Voi è la tensione di fondo
scala dell’i-esimo voltmetro si ripercuotono sulla potenza con un’incertezza globale:
5
EP = ±
1 X
Ci Vi Voi
100R0
(26)
Misure su sistemi trifase
Le possibilità di inserire un wattmetro su una fase di un sistema a più fili sono 3, da cui
per un sistema a tre fili si hanno 9 possibilità di inserzione. Dalla combinazione fasoriale
delle tensioni si dimostra che il numero di inserzioni indipendenti in un sistema a tre fili è 6:
P1(23) = P13 − P12
P2(31) = P21 − P23
(27)
P3(12) = P32 − P31
dal teorema di Aron si dimostra poi che il numero di inserzioni indipendenti in un sistema
a tre fili è 4:
P = P12 + P32 = P23 + P13 = P31 + P21
(28)
Si dimostra poi che la somma delle potenze di due wattmetri con l’amperometrica sul filo
m è uguale a tre volte la potenza assorbita dalla fase m quando le tensioni stellate siano
riferite al baricentro elettrico del sistema. Sviluppando i calcoli si ha:
P12 + P13 = 3Ė10 · I˙1 = 3P10
P12 + P13 = 3Ė10 · I˙1 = 3P10
(29)
P12 + P13 = 3Ė10 · I˙1 = 3P10
Tutte le relazioni esistenti potrebbero essere trasportate alle potenze reattive, misurabili con
varmetri ideali, inseriti nello stesso modo dei wattmetri rispettivi. Vale quindi:
Q1(23) = Q13 − Q12
Q2(31) = Q21 − Q23
Q3(12) = Q32 − Q31
6
(30)
e
Q = Q12 + Q32 = Q23 + Q13 = Q31 + Q21
(31)
Le potenze reattive delle singole fasi in riferimento al centro stella ideale del sistema valgono:
Q12 + Q13 = 3Ė10 × I˙1 = 3Q10
Q12 + Q13 = 3Ė10 × I˙1 = 3Q10
(32)
Q12 + Q13 = 3Ė10 × I˙1 = 3Q10
La validità di queste relazioni si estende alla potenza complessa ma non alla potenza apparente per la quale non sussiste in generale il principio di conservazione.
In un sistema trifase simmetrico nelle tensioni, le potenze reattive possono essere ricavate
da letture wattmetriche. Si ha infatti che
√
V̇23 = −j 3Ė10
(33)
da cui si ricava:
V̇23 · I˙1 =
√
3Ė10 × I˙1 =
√
3Q10
(34)
˙ Si deduce quindi dalle (27):
che deriva dalla relazione j V̇ · I˙ = −V̇ × I.
√
√
√
3Q10 = P13 − P12
3Q20 = P21 − P23
(35)
3Q30 = P32 − P31
ossia la potenza reattiva di una fase, riferita al baricentro elettrico del sistema, è ricavabile,
nel caso di tensioni simmetriche, dalla differenza di due letture wattmetriche che hanno
l’amperometrica inserita sulla fase considerata. Se il sistema delle tensioni concatenate è
√
simmetrico inverso la (33) diviene V̇23 = j 3Ė10 e cambia il segno delle relazioni delle (35).
Si capisce quindi come il segno della potenza reattiva possa essere determinato quando sia
noto il senso ciclico con cui si succedono le fasi e, viceversa, come tale senso ciclico sia
deducibile, una volta noto il segno della potenza reattiva.
7
Misure su sistemi a tre fili
Un sistema trifase simmetrico ed equilibrato è completamente determinato da tre grandezze
indipendenti: una tensione concatenata, una corrente, un angolo di sfasamento. Lo schema
da preferire vede due wattmetri in inserzione Aron e una misura voltmetrica (tre strumenti!).
Ipotizziamo di misurare P12 e P32 , in virtù della simmetria del sistema si ha:
P12 = P23 = P31
P21 = P32 = P13
(36)
per cui la coppia di misure wattmetriche copre tutte le misure wattmetriche realizzabili.
Dalle misure P12 , P32 e V si ha:
P = P12 + P32
√
3(P32 − P12 )
(38)
P 2 + Q2
2 q 2
2
√
P12 + P32
− P12 P32
=√
3V
3V
(39)
Q = 3Q10 =
I=
√
√
(37)
3(P13 − P12 ) =
Il fattore di potenza può essere calcolato oltre che dalla relazione:
cosφ = √
P
3V I
(40)
Il segno da attribuire a una lettura wattmetrica si deduce in primo luogo dalla posizione
dell’indice sullo strumento, quando questo sia correttamente inserito: per valori positivi
l’indice si porta in una posizione interna alla scala, per valori negativi esso tende a spostarsi
al di là della posizione di zero. Si ha tuttavia la possibilità di controllo del segno, partendo da
due wattmetri in inserzione Aron disposti in modo da avere entrambi le letture nell’interno
della scala. Si sconnettono i terminali voltmetrici dal filo comune (ad esempio il 2) e si
collegano rispettivamente con le fasi 3 e 1. Il wattmetro che, nella primitiva inserzione,
indicava P12 segna ora la potenza P13 , mentre quello che indicava P32 ora indica P31 . Per
la simmetria, vedi (36), i wattmetri si sono scambiati le letture. Se entrambe le letture
restano all’interno della scala, le potenze P12 e P32 sono dello stesso segno e quindi positive,
8
altrimenti se gli indici tendono al di là della posizione di zero le due potenze sono di segno
diverso e si assume negativa la lettura minore sotto l’ipotesi che il carico sia passivo. Poiché
ciò accade se il sistema è simmetrico ed equilibrato, contemporaneamente su entrambi gli
strumenti, la verifica può essere effettuata commutando anche una sola voltmetrica. Con
la commutazione di entrambe si ha invece anche la possibilità di controllare se il sistema è
realmente simmetrico ed equilibrato.
Metodo Barbagelata
Nel caso di sistemi simmetrici e squilibrati per cui I1 6= I2 6= I3 la determinazione del sistema
richiede la misura di cinque grandezze indipendenti. Allo scopo esistono numerosi schemi
tra cui lo schema Barbagelata che comprende quattro misure wattmetriche e una misura
voltmetrica. Dalla lettura di due wattmetri in inserzione Aron si ha la potenza attiva totale
del sistema:
P = P12 + P32
(41)
da queste e dalle letture degli altri due wattmetri P13 e P31 si possono ricavare i valori della
altre letture wattmetriche:
P21 = P − P31
P23 = P − P13
(42)
Da questi valori si ricavano le potenze attive e reattive delle singole fasi:
3P10 = P12 + P13
3P20 = P23 + P21
(43)
3P30 = P31 + P32
√
√
3Q10 = P13 − P12
3Q20 = P21 − P23 = P13 − P31
√
3Q30 = P32 − P31
9
(44)
Se interessano le grandezzi globali del sistema si ha:
√
3Q =
√
3(Q10 + Q20 + Q30 ) = P32 − P12 + 2(P13 − P31 )
(45)
Il fattore di potenza globale del sistema è definito dalla relazione:
cosφ = √
P
+ Q2
P2
(46)
Il metodo più semplice per controllare i segni delle letture wattmetriche in un sistema squilibrato, consiste nell’eseguire mediante la commutazione di tre wattmetri tutte le inserzioni
del tipo Pmn . Assumendo come positiva la potenza totale P ed essendo: P = P12 + P32 =
P23 + P13 = P31 + P21 si attribuisce il segno positivo alla lettura maggiore per ognuna delle
tre coppie in inserzione Aron.
Per sistemi a tre fili alimentati da tensioni simmetriche i consumi voltmetrici portano alle
relazioni seguenti:
1V2
V2
+
RW
2 RV
1V2
V2
+
= P32 +
RW
2 RV
′
P12
= P12 +
′
P32
(47)
dove sono evidenti il consumo della wattmetrica e della voltmetrica. Il fattore 0.5 del consumo voltmetrico deriva da considerazioni legate agli sfasamenti tra V̇31 rispetto a V̇12 e
V̇32 .
Assunta C la classe dei due wattmetri, supposti uguali, con valori nominali V0 , I0 e
cosφ0 = 1, il massimo errore assoluto che si può commettere in ognuna delle due letture è:
EW =
C
V0 I0
100
(48)
L’incertezza percentuale corrispondente sulla somma algebrica delle due indicazioni è quindi:
2CV0 I0
ep = ± √
3V Icosφ
(49)
praticamente analoga a quella di un solo wattmetro con le stesse caratteristiche inserito
in un circuito monofase. Viene però a mancare la possibilità di ridurre notevolmente tale
incertezza con gli strumenti per basso cosφ o sovraccaricabili. Infatti al diminuire del fattore
10
di potenza, per esempio in un sistema equilibrato, le due letture non tendono a zero ma ai
valori rispettivamente di +0.5V I e −0.5V I. In questo caso, si ricorre all’inserzione di tre
wattmetri.
Uso dei tre wattmetri
È possibile in base a quanto già osservato determinare la potenza di un sistema trifase a tre
fili mediante l’impiego di 3 wattmetri, collegati rispetto a un punto O comune. La posizione
del centro stella fittizio è indifferente, purché sia la stessa per tutti e tre gli strumenti; spesso
è determinata dalle impedenze dei tre circuiti wattmetrici, che devono per questo rimanere
immutati durante le tre letture. Questo schema consente, nel caso di misura a basso cosφ di
usare strumenti per basso cosphi o sovraccaricabili in modo praticamente analogo a quanto
avviene per i circuiti monofasi. La potenza attiva è data dalla somma delle tre letture.
Scambiando poi due connessioni wattmetriche si ha:
V̇12
P1′ = Ė3 · I˙1 = j √ · I˙1 =
3
V̇23
P3′ = Ė1 · I˙3 = j √ · I˙3 =
3
−Q12
√
3
−Q32
√
3
(50)
da cui segue:
Q = Q12 + Q32
(51)
Metodo Righi o dei tre wattmetri
Sistema simmetrco e squilibrato: wattmetri collegati per leggere P13 , P23 e P3(21) da cui:
P13 = V I1 cos(φ1 − 30◦ )
P23 = V I2 cos(φ1 + 30◦ )
P3(21) = V I3 cos(φ1 − 90◦ )
Sviluppando i passaggi tramite formule trigonometriche si arriva a:
11
(52)
P13 + P23 = P
√
1
3
P13 + P3(21) = P +
Q
2
2
(53)
ossia
Q=
P13 − P23 + 2P3(21)
√
3
12
(54)
Determinazione del senso ciclico
Da fare!
13