Richiami sulla misurazione di potenza elettrica in un
sistema trifase simmetrico e squilibrato
e traccia delle operazioni da svolgere in laboratorio
Alberto Vallan - 2005
1. Il metodo Barbagelata
In un sistema trifase a tre fili simmetrico che alimenta un carico squilibrato le
potenze attive e reattive delle singole fasi e quelle totali possono essere ricavate a
partire esclusivamente da misure di potenza attiva, ricorrendo al metodo
Barbagelata (o delle quattro letture). Questo metodo richiede l’impiego di quattro
wattmetri e un voltmetro e permette di ricavare le nove grandezze che identificano
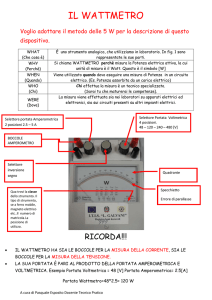
univocamente il sistema trifase oggetto della misurazione. La figura 1 mostra un
possibile schema di misurazione ove sono stati impiegati due amperometi e un
ulteriore voltmetro per controllare che non si sovraccarichino le bobine voltmetriche
e amperometriche dei wattmetri.
Figura 1: Schema di misurazione della potenza con il metodo Barbagelata.
1.1 La misurazione della potenza attiva
La misurazione della potenza attiva totale viene effettuata commutando il deviatore
nella posizione A. E' possibile osservare che i due wattmetri sono collegati secondo
l'inserzione Aron e misurano le potenze P12 e P32, quindi la potenza attiva totale
vale:
P = P12 + P32
(1)
dove con la notazione Pij si indica la potenza misurata da un wattmetro con la la
bobina amperometrica sulla fase i e quella voltmetrica sulle fasi i j.
1
BOZZA ad esclusivo uso del corso di Misure Elettriche 2005/06. Politecnico di Torino
Questa relazione vale per sistemi trifase, a tre fili, simmetrici o dissimmetrici,
equilibrati o squilibrati.
1.2 La misurazione della potenza reattiva
Per misurare la potenza reattiva totale con il metodo Barbagelata sono necessarie 4
misurazioni indipendenti di potenza attiva. Commutando il deviatore sulla posizione
B è possibile misurare le due potenze P13 e P31 che insieme a quelle misurate
precedentemente costituiscono le 4 potenze richieste. La potenza reattiva totale è
data dalla formula
Q=
P12 − P32 + 2( P31 − P13 )
3
(2)
Questa relazione vale per sistemi trifase, a tre fili, simmetrici, equilibrati o
squilibrati.
1.3 La misurazione di altre grandezze di interesse
• Con le potenza attiva totale e la potenza reattiva totale è possibile calcolare il
fattore di potenza complessivo del sistema usando la relazione:
P
cos ϕ =
(3)
2
P + Q2
•
Con le misure delle potenze P12, P32, P13, P31 è possibile ricavare le potenze
attive e reattive di fase P10, P20, P30, Q10, Q20, Q30. A tal fine si devono prima
calcolare le potenze P23 e P21 usando il secondo teorema delle inserzioni
wattmetriche:
(4)
P23 = P − P13 ; P21 = P − P31
Le potenze attive di fase si ricavano con il terzo teorema sulle inserzioni
wattmetriche
P10 =
P12 + P13
3
;
P20 =
P23 + P21
3
; P30 =
P31 + P32
3
(5)
Le potenze reattive di fase si ricavano con il corollario del I teorema sulle
inserzioni wattmetriche
Q10 =
P13 − P12
3
; Q20 =
P21 − P23
3
; Q30 =
P32 − P31
3
(6)
2 Correzione degli effetti sistematici
I principali effetti sistematici sono dovuti all’autoconsumo di wattmetri e voltmetri
e all’errore di fase dei wattmetri.
2
BOZZA ad esclusivo uso del corso di Misure Elettriche 2005/06. Politecnico di Torino
2.1 Autoconsumo
Nello schema di figura 1 le bobine voltmetriche dei wattmetri ed i voltmetri sono
connessi a valle delle bobine amperometriche dei wattmetri. In questa situazione,
trascurando la componente induttiva dell’impedenza della bobina voltmetrica del
wattmetro e di quella del voltmetro, quando il doppio deviatore si trova nella
posizione A i due wattmetri indicano la somma della potenza del carico e della
potenza assorbita dalle bobine voltmetriche. Per il wattmetro collegato tra le fasi 1 e
2 la potenza assorbita dalle voltmetriche vale
PSV 12
V122
≅
RV 12 // RVW 12
(14)
dove: - V12 è la tensione concatenata tra le fasi 1 e 2 (ottenuta con un voltmetro);
- RV12 è la resistenza del voltmetro;
- RVW12 è la resistenza della voltmetrica del wattmetro.
La potenza misurata dal wattmetro connesso tra le fasi 1 e 2 è la somma della
potenza del carico P'12 e dell'autoconsumo:
’
P12 = P12
+ PSV 12
(15)
Analoghe relazioni possono essere ottenute quando il wattmetro è connesso su altre
fasi.
2.2 Errore di fase
Quando si utilizzano wattmetri di tipo elettrodinamico è necessario tener conto di un
altro effetto sistematico che può essere individuato ricordando il principio di
funzionamento di questi strumenti. Uno strumento elettrodinamico è costituito
essenzialmente da una bobina fissa e da una bobina mobile; quando le due bobine
sono percorse da correnti sinusoidali, sulla bobina mobile agisce una coppia, il cui
valor medio è proporzionale al prodotto tra i valori efficaci delle due correnti e il
coseno dell'angolo di sfasamento tra le correnti stesse. Uno strumento di questo tipo
fornisce l'indicazione della potenza attiva assorbita da un carico se una delle due
bobine, solitamente quella fissa, è attraversata dalla corrente che entra nel carico,
mentre l'altra, solitamente quella mobile, è attraversata da una corrente che in
modulo é proporzionale alla tensione presente ai capi del carico. Ciò si ottiene
semplicemente ponendo un resistore di valore opportuno in serie alla bobina mobile.
Tuttavia, poiché‚ la bobina mobile presenta un'induttanza non nulla, la corrente che
attraversa questa bobina risulta sfasata rispetto alla tensione applicata ai suoi capi di
un certo angolo, che per i wattmetri è solitamente indicato con il simbolo ε. La
valutazione dell'effetto di questo fenomeno può essere eseguita osservando che la
potenza misurata da un generico wattmetro risulta
P = VI cos(ϕ − ε ) = P ’ cos ε + Q ’ sin ε
dove: -
3
(16)
P è la potenza attiva misurata dal wattmetro;
V è il valore efficace della tensione presente sulla bobina voltmetrica;
BOZZA ad esclusivo uso del corso di Misure Elettriche 2005/06. Politecnico di Torino
-
I è il valore efficace della corrente che attraversa la bobina
amperometrica;
- ε è l’errore d’angolo del wattmetro;
- ϕ è lo sfasamento tra tensione e corrente presenti sul carico;
- P’ è la potenza assorbita dal carico;
- Q’ è la potenza reattiva assorbita dal carico.
L’angolo ε (espresso in radianti) ha generalmente valori inferiori ad un centesimo
della classe, per cui è lecito approssimare la (16) con
P ≅ P ’ + Q’ε
(17)
L’entità dell'effetto sistematico, dovuto allo sfasamento ε, sulla potenza misurata
vale quindi
PSW ≅ +Q’ε
(18)
Nel caso di misurazioni di potenza con il metodo Barbagelata si dovrebbero
calcolare tali effetti durante le 4 misurazioni, ma questo richiederebbe la conoscenza
delle potenze reattive Q12, Q32, Q13, Q31. Se però i due wattmetri hanno lo stesso
errore d’anglo ε è allora possibile calcolare l’effetto sistematico totale PC :
PC ≅ +Qε
(19)
dove Q è la potenza reattiva calcolata con la (12).
L’effetto dell’errore d’angolo si ripercuote anche sulla potenza reattiva Q. La
correzione da apportare alla potenza Q è calcolabile con le stesse aprrossimazioni
del caso precedente e vale
QC ≅ − Pε
(20)
3 La valutazione dell’incertezza strumentale
L'incertezza della misura di potenza attiva è principalmente legata all'incertezza
strumentale dei wattmetri, quindi alla loro classe. Se si indicano con V0 e I0 le
portate nominali della bobina voltmetrica e di quella amperometrica di un wattmetro
caratterizzato da un fattore di potenza cosϕ0 (quindi di portata V0I0 cosϕ0) e da una
classe c, l'incertezza relativa di misura può essere espressa come:
ε Pc = c
V0 I 0 cos ϕ 0
V I cos ϕ 0
=c 0 0
VI cosϕ
P
(21)
Questa incertezza può essere ridotta impiegando un wattmetro a basso fattore di
potenza, oppure sovraccaricando (per un breve periodo) le bobine voltmetrica e/o
amperometrica del wattmetro entro i limiti indicati dal costruttore.
4
BOZZA ad esclusivo uso del corso di Misure Elettriche 2005/06. Politecnico di Torino
4 Operazioni da svolgere durante l’esercitazione di laboratorio
1. Realizzazione del circuito di misurazione.
2. Stima delle tensione, correnti e potenze che dovranno essere misurate e scelta
delle portate dei rispettivi strumenti.
3. Identificazione del senso ciclico.
4. Esecuzione delle letture degli strumenti nelle due possibili posizioni del doppio
deviatore P12, P32, P13, P31, V12, V32, V13, V31. Se necessario sovraccaricare i
wattmetri controllando che le tensioni e le correnti non superino i limiti
consentiti.
Attenzione : non toccare i contatti durante la misurazione, in quanto le tensioni
presenti nel circuito sono dell’ordine del centinaio di volt.
5. Calcolo degli errori di consumo PSW12, PSW32, PSW13, PSW31 e correzione delle
potenze misurate
P12’ = P12 − PSW 12 ; P32’ = P32 − PSW 32 ; P13’ = P13 − PSW 13 ; P31’ = P31 − PSW 31
6. Calcolo di P e Q totali e corretti dai consumi strumentali (ricordarsi di eventuali
inversioni di polarità)
P ’= P12’ + P32’ ; Q’=
P12’ − P32’ + 2( P31’ − P13’ )
3
7. Stima della correzione dovuta all’errore d’angolo ε
PC = Q’ε ; QC = − P’ε
8. Calcolo della potenza attiva e reattiva corrette dagli effetti dell’errore d’angolo
P ’’= P ’− Pc ; Q’’= Q’−Qc
9. Calcolo del fattore di potenza
cosϕ =
P’’
P’’2 +Q’’2
10. Valutazione dell'incertezza di misura
• Valutare l’incertezza delle misure dirette di potenza
• Valutare l’incertezza di P’’ e Q’’ usando le formule di propagazione ricavate
per i casi notevoli visti a lezione (NdC: se le correzioni degli effetti
sistematici sono piccole allora l’incertezza dovuta alla loro correzione si può
trascurare).
• Calcolare l’incertezza del fattore di potenza (qui dovete usare la formula con
le derivate parziali)
• Altre cause in ordine sparso: temperatura, resistenze dei cavi e dei contatti,
incertezza intrinseca del misurando, stabilità della tensione di rete,
alimentazione non equilibrata, distorsione della tensione di alimentazione….
5
BOZZA ad esclusivo uso del corso di Misure Elettriche 2005/06. Politecnico di Torino
5 Materiale fornito per svolgere l’esercitazione di laboratorio
•
•
Due wattmetri analogici elettromeccanici di tipo elettrodinamico
portate voltmetriche: 125-250-500 V;
portate amperometriche: 2,5-5 A (sovraccaricabilità ammessa 50%);
cosϕ0=1;
classe: 0,2
ε= 0,1;
consumo = 33,3 Ω/V;
campo di frequenza: (15÷60) Hz.
Due voltmetri analogici elettromeccanici di tipo elettromagnetico a ferro
mobile:
portate: 75-150 V;
classe: 0,5;
consumo: 5 VA;
campo di frequenza: (50÷60) Hz;
Due amperometri analogici elettromeccanici di tipo elettromagnetico a ferro
mobile:
portate: 2,5-5 A;
classe: 0,5;
consumo: 2 VA;
campo di frequenza: (50÷60) Hz;
Un doppio deviatore
Alimentazione in corrente alternata trifase simmetrica
Carico trifase squilibrato costituito da due resistori da 100 Ω, 2,5 A e un
condensatore da 20 µF, 450 V
Cavetti per collegamenti
6
BOZZA ad esclusivo uso del corso di Misure Elettriche 2005/06. Politecnico di Torino
•
•
•
•
•