LABORATORIO II

“Le geometrie della visione” Liceo Classico Varrone (Rieti) 2005-2006
LABORATORIO II
 Indice degli elementi del laboratorio
- La nozione di angolo e la sua misura
- Definizione di angolo degli Elementi. Il concetto di tangente, sua definizione trigonometrica.
- Il concetto di luogo geometrico
- Luogo di equidistanza, Ricerca del luogo di equidistanza di due segmenti paralleli e diversi.
- La parabola come caso particolare del luogo di equidistanza presentato
- Dimostrazione analitica e sintetica di un caso di tangenza
- Metodo analitico e sintetico a confronto
Laura Catastini
 Obiettivi disciplinari e formativi della lezione
- Definizione trigonometrica di tangente di un angolo α. Determinazione della misura di un angolo
a partire dalle lunghezze dei lati di un triangolo rettangolo e viceversa. Descrizione della tavola
delle tangenti e del suo uso.
- Definizione di "vedere grande” n gradi, e di “essere grande” n metri. Queste definizioni devono
contribuire a formare concettualmente due campi di esistenza distinti, quello delle forme
geometriche “come sono” e quello delle forme “ come appaiono”
- Il significato logico del “se e solo se” e del “tutti e soli”.
- L’uso di concetti fondamentali della geometria piana quali i criteri di uguaglianza dei triangoli e la
similitudine in problemi applicativi sui nuovi casi riguardanti la geometria della visione
SVOLGIMENTO LABORATORIO
♦ “Essere grande” m metri, “vedere grande” n gradi
Si ricorda la differenza tra l’essere geometrico di una figura e il suo apparire e come questo dipenda
dal punto di vista. Il segmento è la figura più semplice con la quale possiamo schematizzare vari
oggetti reali per i quali una dimensione prevalga sulle altre due. La grandezza effettiva di un
segmento si ottiene misurando la sua lunghezza, mentre la sua grandezza apparente si ottiene
misurando in gradi l’ampiezza dell’angolo visivo. Se A e B sono gli estremi del segmento e se
l’occhio è posto in un punto O dello spazio l’angolo visivo è l’angolo AOB e si dice che il
segmento viene visto da O grande α gradi. La scelta della misura in gradi anziché in radianti aiuta
inizialmente a sottolineare la differenza tra lunghezze reali e lunghezze apparenti.
Poiché è importante misurare la distanza dell’occhio dal segmento per poter stabilire le prime leggi
della visione diretta che legano a questa distanza la grandezza apparente dell’oggetto, viene
ricordata la definizione di distanza di un punto da un segmento che è stata data la lezione
precedente sulla base di una discussione con gli allievi. Questa definizione, scelta come si è visto
tra altre logicamente coerenti, viene utilizzata in tutto il corso e permette di articolare enunciati
precisi suscettibili di dimostrazione o di falsificazione.
♦ La tangente di un angolo
Si introduce la nozione di tangente di un angolo con lo scopo di dare un metodo pratico per
misurare l’ampiezza di un angolo e confrontare tra loro due angoli: ad ogni angolo acuto è associata
biunivocamente e in modo monotono una lunghezza quella della sua tangente.
Definizione di tangente di : La tangente di un angolo acuto è il rapporto tra i segmenti AB e AO,
dove AO è scelto a piacere su uno dei lati dell’angolo α e AB è il segmento di perpendicolare
condotto per A al lato scelto e compreso tra i due lati dell’angolo.
Tan α = AB/OA
E’ apparsa una certa difficoltà a collegare questa definizione di tangente a quella di rapporto tra
seno e coseno: nella nuova definizione (Tavola II-1) gli studenti non hanno individuato come caso
particolare la definizione di tangente come rapporto del seno col coseno che già conoscevano. (non
hanno ancora affrontato in classe i problemi trigonometrici)
Si chiede di dimostrare che questo rapporto non dipende dalla scelta del punto A e neppure dalla
scelta del lato su cui lo si sceglie. Viene evocato dagli studenti, con una certa sicurezza il teorema di
Talete.
La tavola delle tangenti che viene messa a disposizione permette, meglio di una calcolatrice
numerica, di calcolare la tangente di un dato angolo e l’angolo di una data la tangente. Visivamente
la funzione tabulata mostra meglio di una calcolatrice l’andamento qualitativo della funzione
tangente e della sua inversa. L’uso della tavola esemplifica, in semplici problemi, come si utilizza la
trigonometria per “risolvere i triangoli”.
PROBLEMA DELLA PIAZZA (Tavola II-1)
1 - Un osservatore si trova all’interno di una grande piazza quadrata, posto nel punto O. Volgendo
lo sguardo in giro vede i lati della piazza grandi uguali? Giustifica la risposta nel caso (a) e nel caso
(b)
2 - Nel caso (a) quanti gradi viene visto grande il lato AB?
3 - Nel caso (b), se AB = 30 m e O è distante da AB 20 m, quanto vede grande il lato CB? E il lato
AD?
Le risposte ai primi due quesiti vengono date con una certa facilità da tutti. Per il terzo invece si è
aperta una significativa discussione sia sugli aspetti numerici che su quelli teorici. Si intuisce che il
lato CB è visto della stessa grandezza del lato DC e AD grande come AB.
- Perché?
- Perché la figura è simmetrica
Questa prima risposta fornita da una studentessa viene apprezzata e non si insiste ad averne
dimostrazione data la presenza del quadrato con tutte le sue simmetrie note. Si invita invece a dare
altre dimostrazioni: come dimostrare la cosa senza usare le isometrie?
- L’angolo visivo BOC è uguale all’angolo visivo COD quindi sono visti uguali.
- Perché gli angoli sono uguali?
Si fatica a costruire una dimostrazione “euclidea”. Dopo il suggerimento di tracciare per O le
parallele ai lati del quadrato, gli studenti aggiungono in modo autonomo altre linee e la nuova figura
si presenta nel modo seguente
In questa figura vengono individuati i triangoli DOH e BOK che sono evidentemente uguali dato
che sono la metà di due rettangoli uguali. Aggiungendo i triangoli OCH e OCK si ottengono
triangoli uguali perché se a cose uguali si aggiungono cose uguali si trovano cose uguali (nozione
comune).
Questa dimostrazione è fortemente visiva e utilizza solo il fatto che la diagonale di un rettangolo lo
divide in due triangoli uguali.
Dal punto di vista del calcolo, per rispondere al quesito si deve calcolare l’angolo BOC e l’angolo
AOB. Dato che la somma è 180° basta trovarne uno.
Poiché BOC = COK + BOK e COK misura ovviamente 45°, la maggioranza degli studenti si è
concentrata sul calcolo dell’angolo BOK. Si è riscontrato che parte di loro guardavano a tale angolo
come se non variasse al variare di O ed è stato necessario mostrare il contrario con Cabrì. Il
triangolo rettangolo BOK ha il lato OK=30-20=10 m. mentre il lato BK=30-10=20 m.
E’ sorta una difficoltà gestaltica riguardo alla determinazione della tangente dovuta alla posizione
dell’angolo BOK: gli studenti si ostinavano a voler tracciare la perpendicolare relativa al lato OB
ma in quel caso non avevano dati numerici da poter usare e non sono riusciti a cambiare lato, a
scegliere sul lato OK il segmento OK (10 m) e il segmento di perpendicolare KB (20 m) in modo
da stabilire direttamente che tan (BOK) = 2.
La figura “alla rovescia” li ha disorientati ma non fermati e gli studenti sono andati a calcolarsi
l’angolo OBK
Tan(OBK) = OK/KB= 10/20=0,5
Usando la tavola delle tangenti hanno trovato che, in buona approssimazione,
α = 26°40’
Hanno quindi calcolato di seguito che il segmento AB è visto grande 45°+26°40’ = 71°40’.
Maggiori difficoltà per calcolare l’angolo BOC legata a una scarsa comprensione del sistema di
numerazione sessagesimale:
180°- 71°40’= 179°60’-71°40’= 108°20’.
E’ interessante osservare che uno studente ha immediatamente affermato, senza bisogno di
calcolare tangenti:
- l’angolo COB è di 105°
Il motivo è che guardando la figura che preso come dato sicuro che l’angolo BOK fosse di 60°.
L’errore consiste forse nel fatto di essere stato abituato a lavorare solo con angoli di 30°, 45°,60°,
90° e loro supplementari e di aver scelto tra questi quello più ragionevole. La considerazione dello
studente è stata accettata e condivisa dalle due compagne con le quali lavorava a risolvere
l’esercizio, che hanno osservato i loro compagni affannarsi al calcolo di tangenti senza
ripensamenti riguardo alla loro soluzione
PROBLEMA DEL CORRIDOIO (Tavola II-2)
1 - Ponendo l’occhio in O, all’inizio di un corridoio largo 2 m e lungo 6 m, lungo l’asse centrale,
questo verrà visto rettangolare? Giustifica la risposta
2 – Se lo si vuole costruire in modo che, ponendo l’occhio a 1 m di distanza da AB lungo l’asse, il
corridoio venga visto come un rettangolo, quale dovrebbe essere la misura di CD?
L’esercizio non ha presentato particolari difficoltà Il lato AB si vede più grande del lato DC anche
se i due segmenti sono uguali. Alla seconda domanda gli studenti hanno prolungato i segmenti OA
e OB e si sono accorti che, essendo l’angolo AOB di 90°, doveva risultare 16 metri.
Una studentessa ha calcolato anche come si sarebbe dovuto rimpicciolire AB lasciando CD
inalterato e, per calcolare A’B’ ha usato la similitudine dei triangoli ODC e OA’B’ e dalla
proporzione
A’B’ : 1 = 2 : 7
ha concluso che A’B’= 2/7.
♦ Il concetto di luogo geometrico
Si commenta la scheda sui prerequisiti di geometria euclidea (scheda di preliminari ai teoremi
dell’Ottica) e si ricorda cosa sia un luogo geometrico piano: l’insieme di tutti e soli i punti del
piano che verificano una data condizione geometrica. Si stabilisce una convenzione linguistica per
leggere il testo di un problema: se si chiede di determinare un luogo di punti che godano di una
data proprietà, allora basta trovare un insieme di punti che godano tutti della proprietà data. Di tali
insiemi se ne possono trovare più di uno. Se invece viene chiesto di trovare il luogo dei punti che
godono di una data proprietà, allora, data la sua unicità, si sottintende che si richieda il luogo
geometrico. Per esempio, se si chiede un luogo di punti distanti r da un centro O, si può indicare a
piacere un arco della circonferenza C di centro O e raggio r, ma se si chiede il luogo dei punti
distanti r da un centro O allora si deve indicare l’intera circonferenza C. (Per approfondimenti vedi
lezione 3)
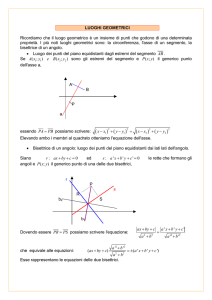
Sono stati presentati come esempi la circonferenza, l’asse di un segmento e la parabola (vedi
Tavola II-3).
Questi due ultimi luoghi intervengono nella determinazione dei punti di equidistanza tra due
segmenti paralleli. Questo esercizio era stato proposto nella lezione precedente e viene ora ripreso e
trattato dettagliatamente.
Tavola II-4
A sinistra della retta per A il luogo è dato dai punti sulla semiretta (rossa) formata dai punti
equidistanti dai due segmenti uguali e paralleli. Alla destra della retta per B il luogo è dato dai
punti dell’asse del segmento AB che sono, in quella zona di piano, equidistanti dai due segmenti.
Nella zona intermedia invece i punti del luogo sono i punti P per i quali PA = PH. Sono cioè i punti
dell’arco di parabola che ha il fuoco in A e come direttrice la retta BH.
Problema: L’asse del segmento AB è tangente alla parabola?
Le risposte degli studenti sono varie ma alla fine si intuisce che l’asse debba essere tangente.
Come dimostrarlo? Gli studenti non riescono a produrre dimostrazioni sintetiche, si ricorda allora
che esiste anche il metodo dimostrativo analitico.
Risoluzione analitica: Il procedimento viene eseguito nel modo seguente. Fissiamo le coordinate
cartesiane come in figura
Il punto A abbia coordinate (0,p) e il punto B =(q,-p). Siano (x,y) le coordinate di un generico punto
P del luogo. Il punto P fa parte del luogo se e solo se
PA=PH
Usando il teorema di Pitagora applicato al triangolo rettangolo APK abbiamo
AP2 = x2 + (p-y) 2
PH2 = (y+p) 2 .
mentre
La condizione geometrica PA = PH equivale alla relazione algebrica
x2 + (p-y) 2 = (y+p) 2
che, sviluppando i calcoli diventa
y = x2 / 4p
Un punto P appartiene al luogo se e solo se le sue coordinate verificano l’equazione precedente.
Questa equazione è l’equazione cartesiana della parabola che ha il fuoco nel punto A = (0,p) e come
direttrice la retta y = – p.
Possiamo ora vedere se l’asse del segmento AB è tangente o meno alla parabola. Una retta è
tangente a una parabola, per definizione, se e solo hanno un solo punto in comune e se la parabola è
interamente contenuta in uno dei due semipiani individuati dalla retta. Nel piano cartesiano se una
parabola ha asse parallelo all’asse y esiste una sola retta che può incontrarla solo in un punto senza
lasciarla interamente in un semipiano, ed è la retta di equazione x = t. Se l’equazione dell’asse del
segmento non ha tale forma e se la risolvente del sistema con l’equazione della parabola ha due
soluzioni coincidenti, allora le curve sono tangenti.
Sviluppiamo il calcolo algebrico.
Il punto D ha q come ascissa e si trova sull’asse del segmento AB: cerchiamo l’equazione dell’asse:
Il punto medio del semento AB è il punto M= (q/2,0) e il coefficiente angolare della retta per AB è
m=-2p/q , l’asse ha dunque equazione
q
q
(x " )
2p
2
Intersecare questa retta con la parabola ,significa analiticamente risolvere il sistema
y=
!
# 4 py = x 2
%
q
q
$
%& y = 2p (x " 2 )
sostituendo la y nella prima equazione otteniamo il sistema equivalente
!
# x 2 " 2qx + q2 = 0
%
q
q
$
%& y = 2p (x " 2 )
che ha la sola soluzione x = q e y = q2/4p che sono proprio le coordinate del punto D. L’asse del
segmento AB non è parallela all’asse della parabola perché non è una retta verticale e interseca la
!
parabola solo nel punto D ciò significa
che questa retta è tangente alla parabola.
Dimostrazione sintetica
Una dimostrazione diversa di questo stesso fatto poteva farsi senza usare le coordinate.
Dimostrazioni di questo tipo a differenza di quella analitica che abbiamo esposto, si chiamano
dimostrazioni sintetiche. La dimostrazione procede per assurdo.
Supponiamo, per assurdo, che sull’asse del segmento FH (che sicuramente non è perpendicolare
alla direttrice) vi sia un ulteriore punto P’ della parabola. Poiché P’ si trova sull’asse del segmento
FH,
P’F=P’H
D’altra parte poiché P si trova anche sulla parabola
P’F = P’H’
Ma allora nel triangolo rettangolo P’HH’ abbiamo l’ipotenusa P’H uguale al cateto P’H’ ma
sappiamo che l’ipotenusa è sempre maggiore dei cateti e quindi c’è contraddizione. Una
dimostrazione del tutto analoga può farsi nel caso che il presunto punto P’ si trovi alla sinistra di P.
Abbiamo visto che è possibile costruire con riga e compasso un numero finito di punti di una
parabola di dato fuoco e data direttrice (scheda 2- 4 spagnolo). Dopo aver trovato per costruzione
un certo numero di punti P del piano appartenente alla parabola P, viene spontaneo unirli
graficamente con una linea continua approssimando così una linea ideale.
Chiediamo di dimostrare sinteticamente che la parallela r all’asse della parabola passante per un
generico punto P costruito con riga e compasso non può contenere altri punti che soddisfano la
condizione che definisce la parabola, cioè che per ogni P’ appartenente ad r si ha che P’F ≠ P’H.
Poiché non è rimasto tempo di dare la dimostrazione in classe, viene lasciato come esercizio su cui
riflettere a casa, dando alcune indicazioni:
- tracciare il segmento FH
- utilizzare uno dei teoremi indicati nella scheda preliminari.
Lo scopo didattico di questo esercizio consiste – dopo aver dimostrato che ogni punto del piano
costruibile in tal modo con riga e compasso gode della proprietà richiesta – nel dimostrare anche
che nessun altro punto del piano gode di tale proprietà – cosa spesso trascurata nelle verifiche di un
luogo geometrico - e nel richiedere l’applicazione di un teorema che servirà nella lezione
successiva, quello del lato maggiore opposto ad angolo maggiore in un triangolo, che in questo
modo verrà rinfrescato.