Limiti di funzioni a +

Limiti di funzioni a +∞
Consideriamo una funzione y = f (x) reale a variabile reale, di dominio
D ⊆ R.
Sia f definita in un intorno di +∞.
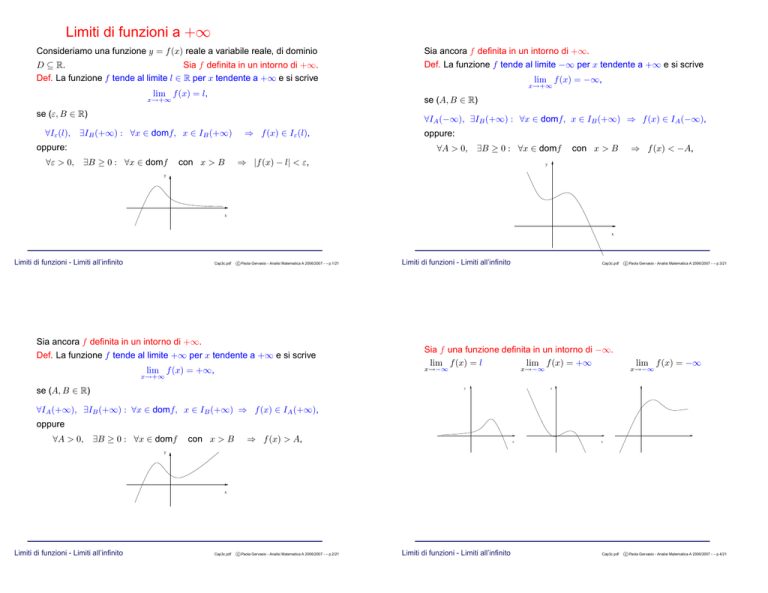
Def. La funzione f tende al limite l ∈ R per x tendente a +∞ e si scrive
lim f (x) = l,
lim f (x) = −∞,
x→+∞
se (A, B ∈ R)
x→+∞
se (ε, B ∈ R)
∀Iε (l),
Sia ancora f definita in un intorno di +∞.
Def. La funzione f tende al limite −∞ per x tendente a +∞ e si scrive
∀IA (−∞), ∃IB (+∞) : ∀x ∈ domf, x ∈ IB (+∞) ⇒ f (x) ∈ IA (−∞),
∃IB (+∞) : ∀x ∈ domf, x ∈ IB (+∞)
⇒ f (x) ∈ Iε (l),
oppure:
oppure:
∀A > 0,
∀ε > 0, ∃B ≥ 0 : ∀x ∈ domf
∃B ≥ 0 : ∀x ∈ domf
⇒ |f (x) − l| < ε,
con x > B
con x > B
⇒ f (x) < −A,
y
y
x
x
Limiti di funzioni - Limiti all’infinito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.1/21
Sia ancora f definita in un intorno di +∞.
Def. La funzione f tende al limite +∞ per x tendente a +∞ e si scrive
lim f (x) = +∞,
Limiti di funzioni - Limiti all’infinito
Cap3c.pdf
Sia f una funzione definita in un intorno di −∞.
lim f (x) = l
lim f (x) = +∞
x→−∞
x→−∞
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.3/21
lim f (x) = −∞
x→−∞
x→+∞
se (A, B ∈ R)
y
y
∀IA (+∞), ∃IB (+∞) : ∀x ∈ domf, x ∈ IB (+∞) ⇒ f (x) ∈ IA (+∞),
oppure
∀A > 0,
∃B ≥ 0 : ∀x ∈ domf
con x > B
⇒ f (x) > A,
x
x
y
x
Limiti di funzioni - Limiti all’infinito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.2/21
Limiti di funzioni - Limiti all’infinito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.4/21
Se invece A è un intervallo in R (oppure A ≡ R), anche un valore finito
x0 può essere un punto di accumulazione per A. Fissato x0 ∈ R,
PSfrag replacements
∀ε > 0 esistono infiniti numeri reali in (x0 − ε, x0 + ε).
lim f (x) = l
x→−∞
∀Iε (l)
∀ε > 0,
∃IB (−∞) :
∃B ≥ 0 :
∀x ∈ domf ∩ IB (−∞)
⇒
∀x ∈ domf con x < −B
A
f (x) ∈ Iε (l)
⇒ |f (x) − l| < ε.
x0
Oss. Quando valutiamo
lim f (x) = +∞
∀A > 0,
∃IB (−∞) :
∃B ≥ 0 :
∞ è un punto di
n→
x→−∞
∀IA (+∞)
lim an ,
∞
R
∀x ∈ domf ∩ IB (−∞)
⇒
∀x ∈ domf con x < −B
f (x) ∈ IA (+∞)
⇒ f (x) > A.
accumulazione per N. Dobbiamo valutare an in un intorno di ∞ e
questo è possibile perchè in tale intorno cadono altri numeri naturali.
Non ha senso calcolare lim an , 5 non è un punto di accumulazione per
n→5
lim f (x) = −∞
N, non posso costruire intorni arbitrari di 5 in cui cadono altri naturali.
x→−∞
∀IA (−∞)
∀A > 0,
∃IB (−∞) :
∃B ≥ 0 :
∀x ∈ domf ∩ IB (−∞)
⇒
∀x ∈ domf con x < −B
f (x) ∈ IA (−∞)
⇒ f (x) < −A.
Posso invece calcolare lim f (x), con f : D ⊂ R → R perchè 5 può
x→5
essere un punto di accumulazione per un insieme A=intervallo ⊂ R.
Limiti di funzioni - Limiti all’infinito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.5/21
Limiti di funzioni - Limiti al finito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.7/21
Punto di accumulazione
Def. Sia A ⊆ R. Diciamo che x0 ∈ R è un punto di accumulazione
Sfrag replacements
per A se in ogni intorno di x0 cade almeno un punto di A diverso da x0 .
A
x0
R
N.B. Consideriamo A = N. L’unico punto di accumulazione per N è
+∞: è l’unico punto di R per cui possiamo costruire un intorno
Sfrag replacements
arbitrario che contenga altri numeri naturali. Infatti:
r
r
Sfrag replacements
A
A
Limiti di funzioni - Limiti al finito
n
r r
R
n
R
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.6/21
Def. Sia A ⊆ R. Un punto di A che non sia un punto di accumulazione
per A è detto punto isolato di A .
Oss. Un punto di accumulazione per A, può anche non appartenere
ad A.
Oss. I punti di N sono tutti punti isolati, l’unico punto di accumulazione
per N è +∞.
Oss. I punti di Z sono tutti punti isolati, punti di accumulazione per Z
sono −∞, +∞.
Oss. Tutti i punti di R sono punti di accumulazione per R.
Limiti di funzioni - Limiti al finito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.8/21
Limite destro e limite sinistro
Limiti di funzione al finito
Sia f una funzione definita in un intorno di x0 ∈ R tranne
eventualmente nel punto x0 .
Def. Si dice che f ha limite finito l ∈ R (o tende ad l) per x tendente
a x0 e si scrive
Sia f (x) = log(x), domf = R+
lim log(x)
Si vuole calcolare
x→1
2
lim f (x) = l
1.5
x→x0
1
y = log(x)
0.5
⇒ |f (x) − l| < ε.
0
y
se
PSfrag
replacements
∀ε > 0, ∃δ > 0 : ∀x ∈ domf : 0 < |x − x0 | < δ
−0.5
y
y = f (x)
l+ε
f (x)
l
PSfrag replacements
−1
−1.5
−2
−2.5
−3
−1
0
1
x
2
3
4
Se x → 1− (x tende a 1 da sinistra), allora y → 0− (ovvero y → 0 dal
basso)
l−ε
Se x → 1+ (x tende a 1 da destra), allora y → 0+ (ovvero y → 0
dall’alto)
x0 − δ x0 x x 0 + δ x
Limiti di funzioni - Limiti al finito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.9/21
Limiti di funzioni - Limiti al finito
N.B. Mi disinteresso del valore di f (x) nel punto x0 . Nel punto x0 la f
Limite destro e limite sinistro
potrebbe assumere qualsiasi valore.
Sto guardando cosa succede per x molto prossimo a x0 .
Consideriamo
funzione:
lim f (x) = l
x→x0
se
∀ε > 0,
∃δ > 0 :
∀x ∈ domf : 0 < |x − x0 | < δ
⇒ |f (x) − l| < ε
∃Iδ (x0 ) :
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.11/21
y

 x
f (x) =
 x+1
un’altra
f
se x ≤ 0
1
se x > 0
x
domf = R
Secondo la terminologia degli intorni:
∀Iε (l)
5
∀x ∈ domf ∩ Iδ (x0 ) \ {x0 }
⇒
f (x) ∈ Iε (l)
Per x → 0 da sinistra le ordinate y = f (x) tendono a zero,
per x → 0 da destra le ordinate y = f (x) tendono a uno
cosa è lim f (x)?.
x→0
Bisogna distinguere se x → 0− (da sinistra) o x → 0+ (da destra).
Limiti di funzioni - Limiti al finito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.10/21
Limiti di funzioni - Limiti al finito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.12/21
Invece di cercare lim f (x), possiamo cercare
Def. Sia f una funzione definita in un intorno destro di x0 , tranne
eventualmente in x0 .
f ha limite destro in x0 uguale a l
x→0
lim f (x)
lim f (x),
e
x→0−
x→0+
ovvero i limiti di f (x) quando x tende a zero da sinistra (x → 0− ) e
PSfrag replacements
quando x tende a zero da destra (x → 0+ ).
0
lim f (x) = l
x→x+
0
se
∀Iε (l)
0− 0+
∃Iδ+ (x0 ) :
∀x ∈ domf, x ∈ Iδ+ (x0 ) \ {x0 }
⇒ f (x) ∈ Iε (l)
oppure
Def. Intorno sinistro di x0 e raggio r > 0 è l’intervallo semiaperto a
sinistra e limitato
∀ε > 0
∃δ > 0 :
∀x ∈ domf,
0 < x − x0 < δ
⇒ |f (x) − l| < ε
Ir− (x0 ) = (x0 − r, x0 ]
Def. Intorno destro di x0 e raggio r > 0 è l’intervallo semiaperto a
destra e limitato
Ir+ (x0 ) = [x0 , x0 + r)
Limiti di funzioni - Limiti al finito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.13/21
Def. Sia f una funzione definita in un intorno sinistro di x0 , tranne
eventualmente in x0 .
f ha limite sinistro in x0 uguale a l
lim f (x) = l
x→x−
0
Limiti di funzioni - Limiti al finito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.15/21
Proposizione
Sia f una funzione definita in un intorno di x0 ∈ R, tranne
eventualmente nel punto x0 .
La funzione f ha limite l in x0 se esistono e coincidono il limite destro
ed il limite sinistro di f in x0 , ovvero:
se
∀Iε (l)
∃Iδ− (x0 ) :
∀x ∈ domf, x ∈ Iδ− (x0 ) \ {x0 }
⇒ f (x) ∈ Iε (l)
oppure
∀ε > 0
∃ lim f (x), ∃ lim f (x) e lim f (x) = lim f (x) = l
∃δ > 0 :
∀x ∈ domf,
0 < x0 − x < δ
⇒ |f (x) − l| < ε
x→x−
0
x→x−
0
x→x+
0
x→x+
0
⇒ lim f (x) = l.
x→x0
Limiti di funzioni - Limiti al finito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.14/21
Limiti di funzioni - Limiti al finito
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.16/21
Funzione continua in un punto
Def. Una funzione f definita in un intorno di x0 ∈ R è continua da
sinistra (risp. continua da destra) in x0 se
Def. Sia x0 ∈ domf . La funzione f si dice continua in x0 se
∀ε > 0,
∃δ > 0 :
∀x ∈ domf : |x − x0 | < δ
lim f (x) = f (x0 )
⇒ |f (x) − f (x0 )| < ε.
x→x−
0
PSfrag replacements
(risp. lim+ f (x) = f (x0 )).
x→x0
y
y
f (x)
ovvero se
∃ lim f (x) = l
x→x0
e
1
l = f (x0 )
1
g(x)
x
esiste il limite di f per x tendente a x0 e questo limite coincide con il
valore della funzione f in x0 .
f (x) =
x≤0
x+1
x>0
g(x) =
x
x
x<0
−x + 1
x≥0
lim f (x) = 0 = f (0) 6= lim f (x) = 1
x→0−
x
x→0+
lim g(x) = 0 6= g(0) = lim g(x) = 1
x→0−
x→0+
Quindi: una funzione f definita in un intorno di x0 è continua in x0 se
e solo se è continua da destra e da sinistra in x0 .
Limiti di funzioni - Funzioni continue
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.17/21
Limiti di funzioni - Funzioni continue
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.19/21
eplacements
y
y
y
f (x)
1
1
x
g(x)
1
x
Def. Sia I un insieme contenuto in domf . La funzione f si dice
continua su I se è continua in ogni punto di I.
h(x)
x
1.5
f (x) = 3x3 + 1,


 x
 x
se x 6= 0
se x ≤ 0
g(x) =
, h(x) =
 1.5 se x = 0
 x + 1 se x > 0
Proposizione. Tutte le funzioni elementari (polinomi, funzioni razionali,
funzioni elevamento a potenza, funzioni trigonometriche, funzioni
esponenziali e loro funzioni inverse) sono continue in tutto il loro
dominio.
lim f (x) = 1 e f (0) = 1 ⇒ f (x) è continua in x0 = 0.
x→0
lim g(x) = 0 mentre g(0) = 1.5
⇒ g(x) NON è continua in x0 = 0.
lim h(x) = 0 e lim+ h(x) = 1
h(x) NON è continua in x0 .
x→0
x→0−
x→0
Limiti di funzioni - Funzioni continue
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.18/21
Limiti di funzioni - Funzioni continue
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.20/21
Riferimenti bibliografici
Canuto-Tabacco: pagg. 74-79, pagg. 83-85.
Sezioni 4.1.1, 4.1.2, pagg. 91-97.
Esercizi
Canuto-Tabacco: pagg. 89: es.2-3.
Calcolare, se possibile, i limiti delle funzioni elementari viste ad
esercitazione per x → −∞ e x → +∞.
Limiti di funzioni - Funzioni continue
Cap3c.pdf
c Paola Gervasio - Analisi Matematica A 2006/2007 - – p.21/21