06/05/14
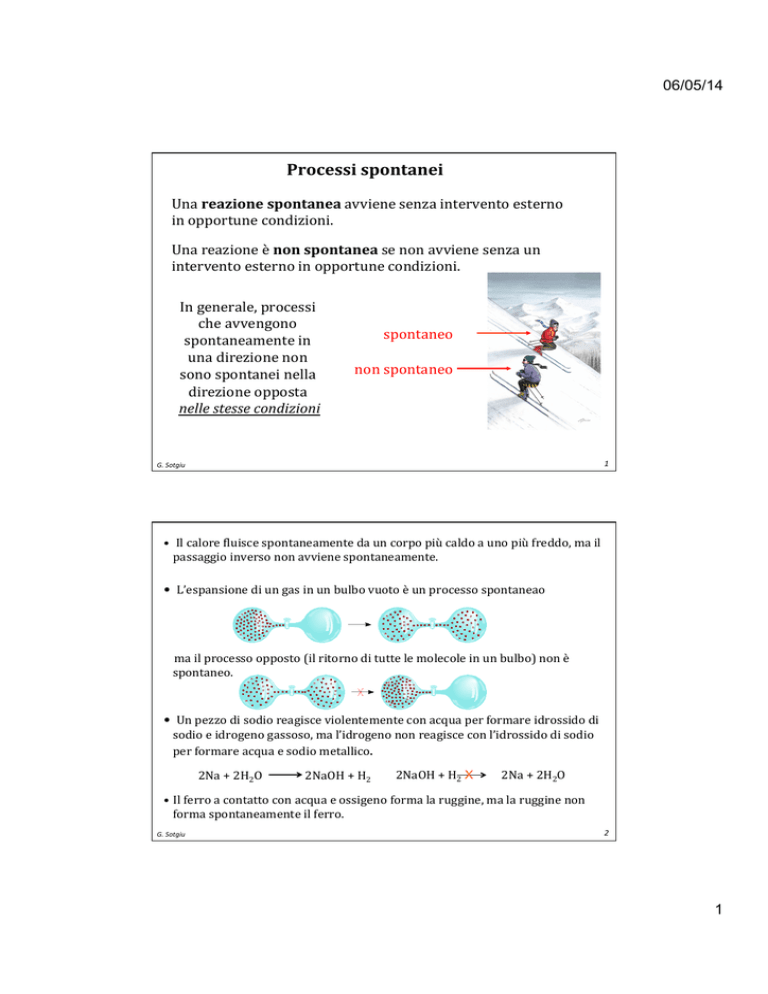
Processi spontanei Una reazione spontanea avviene senza intervento esterno in opportune condizioni. Una reazione è non spontanea se non avviene senza un intervento esterno in opportune condizioni. In generale, processi che avvengono spontaneamente in una direzione non sono spontanei nella direzione opposta nelle stesse condizioni spontaneo non spontaneo 1 G. Sotgiu • Il calore :luisce spontaneamente da un corpo più caldo a uno più freddo, ma il passaggio inverso non avviene spontaneamente. • L’espansione di un gas in un bulbo vuoto è un processo spontaneao ma il processo opposto (il ritorno di tutte le molecole in un bulbo) non è spontaneo. • Un pezzo di sodio reagisce violentemente con acqua per formare idrossido di sodio e idrogeno gassoso, ma l’idrogeno non reagisce con l’idrossido di sodio per formare acqua e sodio metallico. 2Na + 2H2O 2NaOH + H2 2NaOH + H2 X 2Na + 2H2O • Il ferro a contatto con acqua e ossigeno forma la ruggine, ma la ruggine non forma spontaneamente il ferro. G. Sotgiu 2 1
06/05/14
Criterio di Berthelot: Una diminuzione di entalpia signi:ica che la reazione è spontanea Reazioni spontanee CH4 (g) + 2O2 (g) CO2 (g) + 2H2O (l) ΔH0 = –890.4 kJ/mol H+ (aq) + OH-­‐ (aq) H2O (l) ΔH0 = –56.2 kJ/mol Ma H O NH4NO3 (s) 2 NH4+(aq) + NO3-­‐ (aq) ΔH0 = 25 kJ/mol il solo segno del ΔH non è suf:iciente 3 G. Sotgiu 2° Principio della TD
1° P.TD. non pone alcun vincolo al tipo di trasformazioni di energia da una
forma all’altra (ma deve conservarsi l’energia totale)
L’ossevazione
sperimentale ci dice altro
T1
Q1
W
M
Q2
T2
G. Sotgiu W
Q
sempre
Q
W
in particolari condizioni
Si osserva sempre che Q2 < 0
mai Q2 ≥ 0
Q1 non viene trasformato totalmente in W;
una parte (Q2) deve essere ceduta alla sorgente a T
inferiore
W < Q1
impossibilità di trasformare integralmente calore in lavoro
(mantenendo costante lo stato del STD)
4 2
06/05/14
2° Principio della TD
Se il processo non è ciclico si può avere Q = W (es: espansione
isoterma di un gas),
MA
questo non è l’unico risultato finale, cioè si ha anche una
variazione dello stato del S.TD.
Inoltre
tra due S.TD. a T diversa posti a contatto c’è sempre cessione di
calore dal S.TD. più caldo a quello più freddo: il calore non passa
MAI da quello freddo a quello caldo!
ESSENZA
è sempre possibile convertire completamente energia "ordinata" in
energia "disordinata", l'opposto può essere ottenuto solo a spese di
un ulteriore sforzo organizzativo.
5 G. Sotgiu 2° Principio della TD
Enunciato di KELVIN:
è impossibile realizzare una trasformazione il cui unico risultato
finale sia la conversione in lavoro del calore estratto da un
sistema che si mantiene a temperatura costante
Enunciato di CLAUSIUS:
è impossibile realizzare una trasformazione il cui unico risultato
finale sia il trasferimento di calore da un corpo ad una data
temperatura ad un altro a temperatura più elevata
Conseguenza: è vietato un moto perpetuo di seconda specie,
cioè la possibilità di estrarre calore da una sorgente a
temperatura T1 e di trasformarlo in lavoro meccanico senza
l’intervento di di una seconda sorgente a temperatura più bassa
G. Sotgiu 6 3
06/05/14
2° Principio della TD
Per una trasformazione ciclica isoterma (cioè un ciclo che si compie utilizzando una sola sorgente, T = cost.) deve essere (per il 2° P.TD.) i m p o s s i b i l e r e a l i z z a r e u n a Q ≤ 0 non è possibile assorbire è trasformazione il cui unico risultato :inale sia la conversione in lavoro del e W ≤ 0 calore e produrre lavoro calore estratto da un sistema che si mantiene a temperatura costante cioè: o il S.TD. subisce lavoro dall’ambiente e cede calore alla sorgente ===> trasformazione integrale W–––> Q oppure Q = 0 e quindi W = 0 no scambi energetici Se il ciclo monotermo è reversibile e viene percorso in senso inverso, allora dovrebbe essere Q ≥ 0 e W ≥ 0 ma poiché il segno > è impossibile, allora solo Q = 0 e W = 0 differenza reversibilità ≠ irreversibilità 7 G. Sotgiu Trasformazioni cicliche T1
Ciclo termico se durante un ciclo si produce lavoro assorbendo calore (da sorgenti esterne) Q1
M
Q2
T2
Ciclo frigorifero se durante un ciclo è richiesto lavoro esterno per estrarre calore da una serie di sorgenti fredde per cederle a sorgenti calde G. Sotgiu W
T1
QC
W
M
Q0
T2
8 4
06/05/14
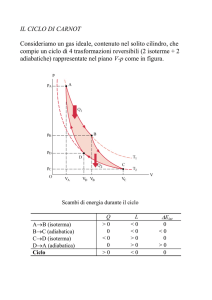
CICLO DI CARNOT trasformazione ciclica reversibile di un S.T.D. costituito da due isoterme e due adiabatiche che, alternandosi, portano il S.T.D. da una temperatura T1 ad una temperatura T2 (T2 < T1) per tornare in:ine alla T1 9 G. Sotgiu CICLO DI CARNOT A⎯> B isoterma a T1; B ⎯> C adiabatica (da T1 a T2 con T2 < T1); C ⎯> D isoterma a T2; D ⎯> A adiabatica (da T2 a T1) G. Sotgiu 10 5
06/05/14
CICLO DI CARNOT A⎯> B isoterma a T1; lavoro compiuto dal S.T.D. W1 assorbendo il calore Q1 dal serbatoio a T1 B ⎯> C adiabatica; lavoro compiuto dal S.T.D. W2 C ⎯> D isoterma a T2; lavoro subito dal S.T.D. W3 cedendo il calore Q2 al serbatoio a T2 D ⎯> A adiabatica; lavoro subito dal S.T.D. W4 11 G. Sotgiu CICLO DI CARNOT • Energia interna: ∆U = 0 per un ciclo • Calore messo in gioco dal S.T.D.: QTOT = Q1 + Q2 • Lavoro messo in gioco dal S.T.D. : WTOT = W1 + W2 + W3 + W4 (area racchiusa dalla curva) QTOT = WTOT G. Sotgiu 12 6
06/05/14
CICLO DI CARNOT RENDIMENTO: si de:inisce come rendimento η di un ciclo termodinamico il rapporto tra il lavoro compiuto W ed il calore assorbito Q1 Q
W
Q + Q2
Q2 < 0
η = TOT = 1
= 1− 2
Q1
Q1
Q1
de:inizione di rendimento applicabile per qualsiasi S.TD. e per qualsiasi trasformazione reversibile ed irreversibile 13 G. Sotgiu CICLO DI CARNOT A ––> B (espansione isoterma) dU=0
Calore assorbito nell’espansione isoterma (a T1)
Q1 = nRT1lnVB/VA = W1
dW = pdV = nRTdV/V
per trasformazioni
reversibili e gas perfetto
B ––> C (espansione adiabatica) [T·V(γ – 1)]
Q=0
T2·VC(γ – 1) = T1·VB(γ – 1)
W2 = – ΔUBC = n·cv·(T1 – T2)
G. Sotgiu 14 7
06/05/14
CICLO DI CARNOT
C ––> D (compressione isoterma)
Calore ceduto nella compressione isoterma (a T2)
Q2 = nRT2lnVD/VC = W3
W3 < 0
VD < VC
D ––> A (compressione adiabatica) [T·V(γ – 1)]
Q=0
T1·VA(γ – 1) = T2·VD(γ – 1)
W4 = – ΔUDA = n·cv·(T2 – T1) = – W2
15 G. Sotgiu CICLO DI CARNOT
Per l’intero ciclo
Q = Q1 + Q2 = W = W1 + W2 + W3 + W4 = W1 + W3
η=
€
W Q1 + Q2
nRT2 ln(VD /VC )
T ln(VC /VD )
=
= 1+
=1− 2
Q1
Q1
nRT1 ln(VB /VA )
T1 ln(VB /VA )
Poichè
η = 1−
€
G. Sotgiu VD < VC
Per trasformazioni adiabatiche TV(γ-1) = cost
T1VA(γ-1) = T2VD(γ-1)
T1VB(γ-1) = T2VC(γ-1)
VB VC
=
VA VD
T2
T1
rapporto:
VB(γ −1) VC(γ −1)
=
VA(γ −1) VD(γ −1)
T2 < T1
€
16 €
8
06/05/14
CICLO DI CARNOT
η =1−
€
Q2
T
=1− 2
Q1
T1
T2 < T1
per un gas perfetto
e trasf. reversibili
Teorema di Carnot (dimostrabile)
Tutte le macchine termiche reversibili che lavorano tra la stessa
temperatura superiore T1 ed inferiore T2 hanno lo stesso rendimento; il
rendimento non dipende quindi nè dal S.TD. nè dalle trasformazioni
che compongono il ciclo (ma devono essere reversibili)
Per macchine irreversibili
dato che dWrev > dWirr
ηrev > ηirr (sempre tra T1 e T2)
17 G. Sotgiu Ciclo di Stirling
A
trasformazione ciclica reversibile di un S.T.D.
costituito da due isoterme e due isocore che,
T1
alternandosi, portano il S.T.D. da una
B
D
T2
C
temperatura T1 ad una temperatura T2 (T2 < T1)
per tornare infine alla T1
A ⎯> B isoterma a T1; Q1 = W1 = nRTlnVB/VA
C ⎯> D isoterma a T2; Q3 = W2 = nRTlnVD/VC
Isocore: V=cost. quindi pdV=0 W=0 dU=dQ=ncvdT
B ⎯> C isocora; Q2 = ncvΔT=ncv(T2-T1)
D ⎯> A isocora; Q4 = ncvΔT=ncv(T1-T2)
Per l’intero ciclo
Q = Q1 + Q2 + Q3 + Q4 = W = W1 + W2
η=
G. Sotgiu Q4 = – Q2
quindi W= Q1 + Q3
W Q1 + Q3
nRT2 ln(VD /VC )
T ln(VC /VD )
T
=
= 1+
=1− 2
=1− 2
Q1
Q1
nRT1 ln(VB /VA )
T1 ln(VB /VA )
T1
18 €
9
06/05/14
Ciclo frigorifero
T1
QC
macchina che, subendo lavoro, permette
W
di trasferire calore da una sorgente a
bassa temperatura ad un’altra a più alta
M
Q0
temperatura
T2
Efficienza di un ciclo frigorifero
ξ=
ξ=
Q0
W
Q0
Q0
nRT2 ln(VC /VD )
T2
=
=
=
W
Q0 + QC nRT1 ln(VB /VA ) − nRT2 ln(VC /VD ) T1 − T2
€
Il calore QC ceduto dalla macchina alla sorgente a temperatura maggiore (T1)
€
sarà sempre maggiore di quello assorbito Q0 dalla sorgente fredda (T2)
19 G. Sotgiu CICLO DI CARNOT
η =1−
€
Q2
T
=1− 2
Q1
T1
Teorema di Carnot (dimostrabile)
Tutte le macchine termiche reversibili che lavorano
tra la stessa temperatura superiore T1 ed inferiore T2
hanno lo stesso rendimento; il rendimento non
dipende quindi nè dal S.TD. nè dalle trasformazioni
che compongono il ciclo (ma devono essere
reversibili)
lavoro
massimo
per un gas perfetto
e trasf. reversibili
T2 < T1
P
V
Per macchine irreversibili
dato che dWrev > dWirr
ηrev > ηirr (sempre tra T1 e T2)
G. Sotgiu 20 10
06/05/14
Temperatura Termodinamica
η =1−
Q2
T
=1− 2
Q1
T1
Q2 T2
=
Q1 T1
€
Teorema di Carnot: η non dipende dal S.TD.
sono le temperature della sorgente calda e di
quella fredda a determinare il η
rapporto funzione solo di T1 e T2
η utilizzato per definire le temperature delle sorgenti
se T2 à 0 allora η à 1
Zero assoluto: temperatura alla quale una trasformazione
isoterma avviene senza scambio di calore
21 G. Sotgiu Proprietà dei cicli
Teorema di Clausius
Per una trasformazione ciclica reversibile
Q2 T2
=
Q1 T1
in generale
€
€
Q1 Q2
=
T1 T2
∑
Qi
=0
i T
i
€
∫
Q1 Q2
−
=0
T1 T2
dQ
=0
T
rev
rev
se la trasformazione è irreversibile
€ηrev > ηirr
Qi
∑€T
i
i
<0
∫
dQirr
<0
T
G. Sotgiu €
€
€
Q
=S
T
22 11
06/05/14
Funzione Entropia
Per una trasformazione ciclica reversibile
Q2 T2
=
Q1 T1
Q1 Q2
=
T1 T2
Studiamo il comportamento della
Q
= S funzione S nel ciclo di Carnot
T
A –––> B (trasformazione isoterma reversibile )
€
Q
Q1 > 0
ΔSA −>B = 1 > 0
T1
€
€–––> C (trasformazione
B
adiabatica reversibile )
∆SB––>C = 0
Q=0
C –––> D (trasformazione isoterma reversibile )
€
ΔSC −>D =
Q2
<0
T2
Q2 < 0
D –––> A (trasformazione adiabatica reversibile )
∆SDàA = 0
Q=0
23 G. Sotgiu €
Funzione Entropia
A –––> B (trasformazione isoterma reversibile )
ΔSA −>B =
Q1
>0
T1
Q1 > 0
B –––> C (trasformazione adiabatica reversibile )
∆SB––>C = 0
Q=0
C –––> D (trasformazione isoterma reversibile )
€
ΔSC −>D =
Q2
<0
T2
Q2 > 0
D –––> A (trasformazione adiabatica reversibile )
∆SDàA = 0
Q=0
ΔS = ∑1 ΔSi =
€
G. Sotgiu Q1 Q2
−
=0
T1 T2
24 €
12
06/05/14
Funzione Entropia
ΔS = ∑1 ΔSi =
Q1 Q2
−
=0
T1 T2
Applicabile a qualsiasi ciclo reversibile (dimostrazione grafica)
Per scambi di calore reversibili ma infinitesimi
€
" dQ %
dS = $ '
# T & rev
ΔSciclo =
∫
dQrev
=0
T
Funzione di stato ====> ENTROPIA
B
SB€– SA =
€
∫
A
dQrev
T
per qualsiasi percorso tra
A e B purchè reversibile
25 G. Sotgiu €
Funzione Entropia
p
irr
A
B
B
rev
€
V
∫
B
A
# dQ &
# dQ &
∫ %$ T (' + ∫ %$ T (' =
irr
rev
A
B
dQ
=
T
B
B
" dQ %
" dQ %
∫ $# T '& – ∫ $# T '& < 0
irr
rev
A
A
" dQ %
' – (SB – SA ) < 0
& irr
A
€ B
# dQ &
ΔS = SB – SA = ∫ % ( >
$ T ' rev
A
∫ $# T
€
G. Sotgiu B
# dQ &
(
' irr
A
∫ %$ T
26 €
13
06/05/14
Funzione Entropia
p
irr
B
A
rev
" dQ %
" dQ %
dS = $ ' > $ '
# T & rev # T & irr
V
Disuguaglianza di Clausius €
Per un sistema isolato dQ = 0
per reversibili ∆S = 0
per irreversibili ∆S > 0
∆S ≥ 0
27 G. Sotgiu Funzione Entropia
Ciclo di Carnot nel piano S vs T
T
A
B
D
C
S
G. Sotgiu 28 14
06/05/14
De:inizione statistica di Entropia Microstati che derivano dalla combinazione di due dadi e i corrispondenti macrostati. Il macrostato più probabile ha un elevatissimo numero di microstati rispetto agli altri macrostati. 29 G. Sotgiu Microstati, Entropia, e il Secondo Principio della Termodinamica Alcuni modi possibili di distribuire quattro molecole in due scompartimenti uguali. L’entropia è una misura del numero dei possibili microstati possibili per il sistema per dare un macrostato Variazione di entropia
G. Sotgiu 30 15
06/05/14
Terzo principio della termodinamica: Stabilisce che l’entropia di una sostanza pura nella sua forma termodinamicamente più stabile è zero a zero kelvin, indipendentemente dalla pressione. Variazioni di temperatura Entropie assolute Entropie assolute per mole di materiale misurate a pressione normale di 1 bar sono dette entropie molari standard, e sono indicate con So. 31
L’aumento di entropia di una sostanza a pressione
costante dallo zero assoluto al suo stato gassoso a
una data temperatura.
Transizioni di fase
G. Sotgiu 32 16
06/05/14
Entropia residua: valore di entropia a 0 K per sistemi nei
quali il terzo principio della termodinamica non è
applicabile.
Cristallo ideale
S = 0 a 0 K.
Cristallo reale
Difetti
nell’orientazione
S > 0 a 0 K.
sperimentalmente
G. Sotgiu 33 Dal Secondo Principio della Termodinamica:
L’entropia di un sistema isolato aumenta durante un
processo spontaneo e rimane costante durante un
processo all’equilibrio (reversibile)
Processo spontaneo
Processo reversibile (o all’equilibrio)
Se ΔSuniv è negativo, il processo non è spontaneo nella
direzione indicata. E’ invece spontaneo nella direzione
opposta.
G. Sotgiu 34 17
06/05/14
Processi che
portano a un
aumento di
entropia
(ΔS > 0)
35 G. Sotgiu Spontaneità e Energia libera di Gibbs
Spontaneità nei sistemi non isolati
P costante
G. Sotgiu 36 18
06/05/14
Variazione di entropia nell’ambiente (ΔSamb)
Processo esotermico
ΔSamb > 0
Processo endotermico
ΔSamb < 0
Energia libera di Gibbs
Criterio di spontaneità a P e T
costante
37 G. Sotgiu Energia libera di Gibbs e lavoro non di espansione
ΔU = q + w
G. Sotgiu 38 19
06/05/14
Dipendenza dalla temperatura di ΔG
ΔH e ΔS entrambe +, ΔG sarà + a basse temperature (dove predomina il
fattore entalpico) e diventa – ad alte temperature (dove predomina il fattore
entropico).
La temperatura alla quale ΔG inverte il segno da + a - (quando ΔH = T ΔS)
dipende dai valori di ΔH e ΔS.
ΔH + e ΔS -, ΔG sarà sempre positivo indipendentemente dalla
temperatura.
ΔH - e ΔS +, ΔG sarà sempre negativo indipendentemente dalla
temperatura.
ΔH e ΔS entrambi -, ΔG sarà – a basse temperature (dove predomina il
fattore entalpico) e diventa + ad alte temperature (dove predomina il
fattore entropico). La temperatura alla quale ΔG inverte il segno da – a +
(quando ΔH = T ΔS) dipende dai valori di ΔH e ΔS.
G. Sotgiu 39 20