ENTROPIA E SECONDO PRINCIPIO DELLA TERMODINAMICA
(Prof. Euro Sampaolesi – Liceo G. Leopardi di Recanati)
η ≤ ηc
1. Teorema di Carnot
:
il rendimento η di una macchina termica è sempre minore (per una qualsiasi macchina termica
reale irrversibile) o uguale (per una qualsiasi macchina termica ideale reversibile) al rendimento
ηc di una macchina termica ideale reversibile che lavora su un ciclo di Carnot.
2. Ciclo di Carnot:
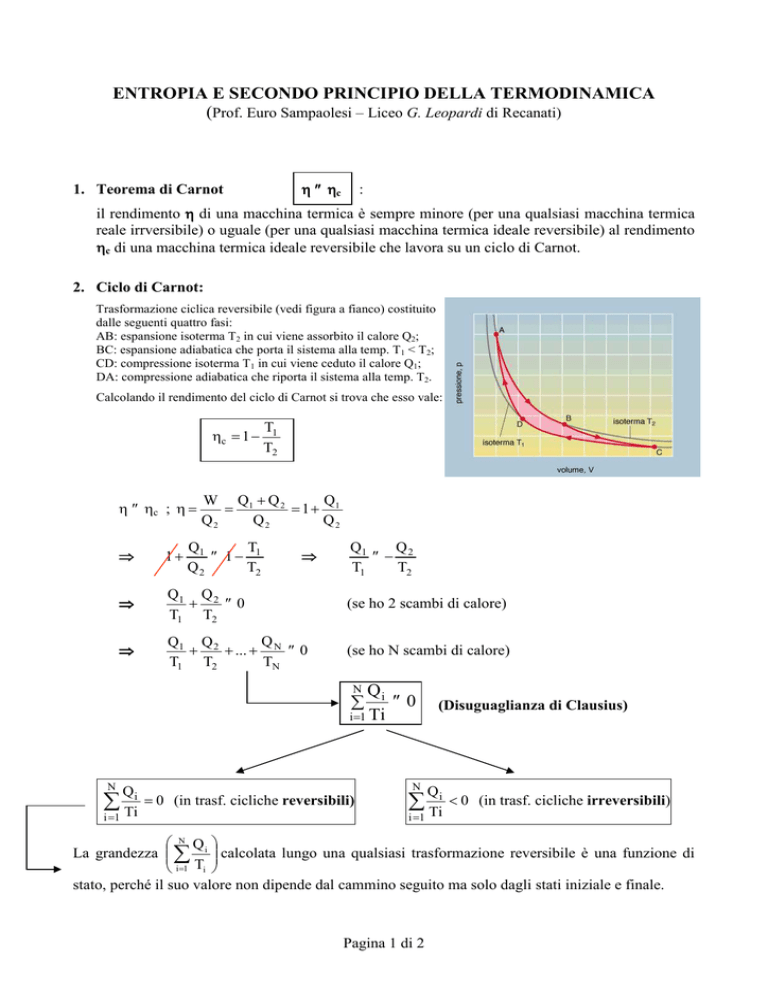
Trasformazione ciclica reversibile (vedi figura a fianco) costituito
dalle seguenti quattro fasi:
AB: espansione isoterma T2 in cui viene assorbito il calore Q2;
BC: espansione adiabatica che porta il sistema alla temp. T1 < T2;
CD: compressione isoterma T1 in cui viene ceduto il calore Q1;
DA: compressione adiabatica che riporta il sistema alla temp. T2.
Calcolando il rendimento del ciclo di Carnot si trova che esso vale:
ηc = 1−
η ≤ ηc ; η =
T1
T2
Q
W Q1 + Q 2
=
= 1+ 1
Q2
Q2
Q2
Q1
T
≤ 1− 1
Q2
T2
Q1
Q
≤− 2
T1
T2
⇒
1+
⇒
Q1 Q 2
+
≤0
T1 T2
(se ho 2 scambi di calore)
⇒
Q
Q1 Q 2
+
+ ... + N ≤ 0
T1 T2
TN
(se ho N scambi di calore)
⇒
Qi
≤0
i =1 Ti
N
∑
N
Q
∑ Tii = 0 (in trasf. cicliche reversibili)
i =1
N
(Disuguaglianza di Clausius)
Q
∑ Tii < 0
(in trasf. cicliche irreversibili)
i =1
N Q
La grandezza ∑ i calcolata lungo una qualsiasi trasformazione reversibile è una funzione di
i=1 Ti
stato, perché il suo valore non dipende dal cammino seguito ma solo dagli stati iniziale e finale.
Pagina 1 di 2
Definizione di ENTROPIA (S):
Re v
NQ
∆S = S( B) − S( A ) = ∑ i
,
T
=
i
1
i
A→ B
dove ∆S è la variazione di entropia dal valore dello stato iniziale S(A) a quello dello stato finale
S(B) calcolata lungo una qualsiasi trasformazione reversibile (Rev) A→B*; Qi è il valore del calore
scambiato alla temperatura Ti nell’ i-esimo stadio intermedio in cui è scomposto il cammino
reversibile A→B a cui corrisponde una variazione di entropia ∆Si = Q i Ti .
In una trasformazione reversibile a temperatura costante T dove viene scambiato il calore Q la
variazione di entropia è espressa dalla formula:
∆S =
Q
T
(l’entropia è una grandezza scalare che si misura in Joule/Kelvin)
* posso calcolare il valore lungo una trasformazione reversibile qualsiasi, perché abbiamo dedotto
N Q
dalla disuguaglianza di Clausius (pagina precedente) che la grandezza ∑ i è una funzione di
i=1 Ti
stato, quindi l’entropia è una funzione di stato.
Consideriamo un sistema isolato che subisce una generica trasformazione ciclica ABA costituita da
una fase irreversibile (Irr) A→B e una fase reversibile (Rev) B→A (vedi figura sotto) e scriviamo la
disuguaglianza di Clausius per questo ciclo:
Irr
Re v
N Qi
N Qi
+
≤0
∑
∑
i =1 Ti A → B i =1 Ti B→ A
A
Irr
Irr
Rev
N Qi
+ S( A ) − S( B) ≤ 0
∑
i =1 Ti A → B
B
Irr
NQ
S( B) − S( A) = ∆S ≥ ∑ i
i =1 Ti A → B
ma un sistema isolato non scambia calore con l’esterno, quindi Qi = 0
⇒
∆S ≥ 0
cioè nelle trasformazioni reversibili (ideali) l’entropia rimane costante, mentre
nelle trasformazioni irreversibili (reali) che avvengono in un sistema isolato**
l’entropia aumenta sempre !!!
Questa disuguaglianza è un altro modo di esprimere il Secondo Principio della Termodinamica:
un sistema isolato evolve spontaneamente verso stati di massima entropia !!
** l’intero universo è un sistema isolato in quanto non esiste nessun ambiente esterno con cui può
scambiare calore, quindi si dice che l’entropia dell’universo aumenta sempre !!!
Pagina 2 di 2












