Termodinamica 8

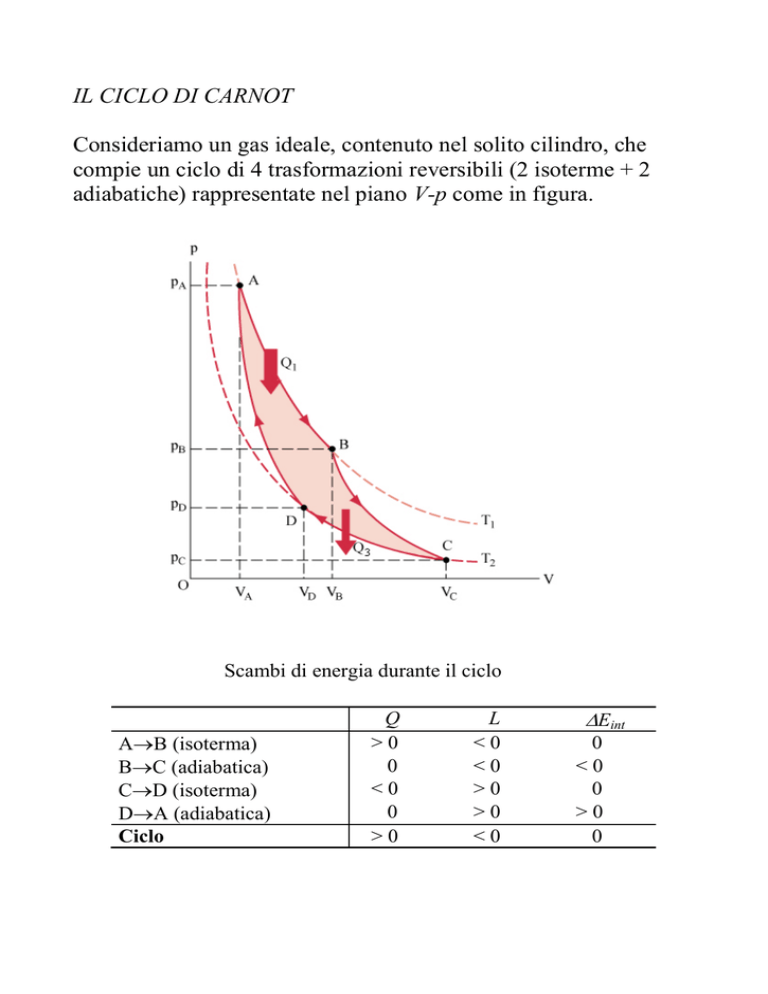
IL CICLO DI CARNOT
Consideriamo un gas ideale, contenuto nel solito cilindro, che
compie un ciclo di 4 trasformazioni reversibili (2 isoterme + 2
adiabatiche) rappresentate nel piano V-p come in figura.
Scambi di energia durante il ciclo
AB (isoterma)
BC (adiabatica)
CD (isoterma)
DA (adiabatica)
Ciclo
Q
>0
0
<0
0
>0
L
<0
<0
>0
>0
<0
Eint
0
<0
0
>0
0
Nell’isoterma da A a B si ha:
Q1  L1  n R T1 ln
VB
VA
dove il lavoro è quello fatto dal gas che si espande.
Nell’isoterma da C a D si ha:
Q3  L3  n R T2 ln
VC
VD
Dividendo membro a membro le precedenti equazioni si ha:
Q1 T1 ln (VB VA )

Q3 T2 ln (VC VD )
(16)
Per le due trasformazioni adiabatiche B  C e D  A,
ricordando l’equazione:
T V  1  costante
si può scrivere:
T1 VB 1  T2 VC 1
T1 VA 1  T2 VD 1
che, divise membro a membro, danno:
VB  1 VC  1
  1
 1
VA
VD

VB VC

VA VD
Sostituendo quest’ultima equazione nella (16), si ottiene:
Q1 T1

Q3 T2
(17 )
Il rendimento di un motore che opera con un ciclo di Carnot
vale quindi:
e  1
Qc
T
1 2
Qa
T1
essendo Q3 = Qc il calore ceduto e Q1 = Qa quello assorbito
durante il ciclo.
Si può concludere che:
il rendimento di una macchina di Carnot dipende solo dalle
temperature dei due termostati tra i quali essa opera.
Siccome T2 > 0 K, il rendimento non può mai essere pari al
100%.
I normali motori termici usano come sostanza di lavoro il
vapore o una miscela di combustibile ed aria.
Teorema di Carnot e secondo principio
Supponiamo per assurdo che esista una generica macchina
termica G il cui rendimento (eG) sia maggiore di quello (eC )
della macchina reversibile di Carnot R. Facciamo lavorare la
macchina G tra i due stessi termostati tra cui opera la
macchina di Carnot R (v. figura (a)) e supponiamo che:
QCG  QCR
(a)
(b)
eG  eR  LG  LR  QFG  QFR
Essendo il motore di Carnot reversibile, lo si può far operare
da frigorifero che sfrutta parte del lavoro LG per funzionare (v.
figura (b)): la restante parte è lavoro positivo compiuto
sull’ambiente.
La macchina risultante in figura (b) (motore generico +
frigorifero di Carnot) non scambia calore netto con il
termostato caldo.
La macchina risultante si comporta come un motore che
assorbe dal termostato freddo una quantità (positiva) di
calore:
Q  QFR  QFG ,
compiendo sull’ambiente un lavoro (positivo):
L  LG  LR
Conclusione:
La macchina risultante si comporta come motore perfetto
capace di trasformare integralmente in lavoro il calore
assorbito da un’unica sorgente, violando il secondo principio.
Di conseguenza non può che essere:
eG  e R
Se G fosse anch’essa reversibile, il ragionamento può essere
ripetuto scambiando i ruoli delle due macchine (G funziona
da frigorifero ed R da motore); se concluderebbe che:
eG  eR
Quindi, se entrambe le macchine sono reversibili, non resta
che la possibilità:
eG  eR
Abbiamo quindi dimostrato che:
date due sorgenti a temperatura TC e TF, un motore termico
qualunque funzionante tra tali temperature avrà rendimento
minore o uguale a quello della macchina di Carnot
funzionante tra le stesse temperature, valendo l’uguaglianza
solo se il motore è anch’esso reversibile.
(Teorema di Carnot)
L’ ENTROPIA
Si consideri un ciclo di Carnot. Per tale ciclo la (17) si può
scrivere come:
Qa
Q
 c
T1
T2
essendo Q3 = Qc il calore ceduto e Q1 = Qa quello assorbito
durante il ciclo.
Dato che Qa e Qc hanno segni sempre opposti (sia per un
motore che per un frigorifero), la precedente diviene:
Qa Qc

0
T1 T2
Indicando con Qi il calore assorbito o ceduto dal sistema
quando questo si trova ad una temperatura Ti, si può riscrivere
la precedente come:
2

i 1
Qi
0
Ti
(18)
Si vuole ora generalizzare l’equazione precedente
considerando un qualsiasi ciclo reversibile. Per fare questo
approssimiamo tale ciclo reversibile, mostrato nel riquadro (a)
della seguente figura, come un insieme di cicli di Carnot,
mostrati nel riquadro (b) della stessa figura.
Compiere in sequenza ognuno dei cicli nel riquadro (b) della
figura precedente equivale (in termini di calore e lavoro) a
compiere non il ciclo in esame ma il ciclo costituito dalla
serie di linee frastagliate che approssima il ciclo reale.
Per la sequenza di isoterme e adiabatiche di cui sopra la
generalizzazione della (18) porta a scrivere:

i
Qi
0
Ti
Rendendo progressivamente più piccoli gli intervalli di
temperature tra due isoterme successive, si può approssimare
sempre meglio il ciclo reale con una sequenza di adiabatiche e
isoterme. Per differenze infinitesime di temperatura (e quindi
per quantità infinitesime di calore scambiate) la precedente
diventa, al limite:

dQ
0
T
(19)
Siccome il cammino chiuso è generico, la (19) implica
l’esistenza di una funzione di stato S chiamata entropia di cui
dQ / T è il differenziale esatto. Ossia:
dS 
dQ
T
(20)
N.B.: Sebbene dQ non sia un differenziale esatto, dQ / T lo è.
L’entropia come parametro di stato
Già sappiamo che, se una grandezza X è una funzione di stato,
allora l’integrale:
 dX
calcolato tra due stati di equilibrio ha lo stesso valore per tutte
le trasformazioni (reversibili) che collegano quei due stati.
Verifichiamo questa proprietà per la funzione di stato
entropia.
Per la (20), la (19) assume la forma:
 dS
0
Facendo riferimento alla figura a
destra, si può allora scrivere:

B
A
dS   dS 
A

(1)
(2)
B
dS  0
dove il primo integrale è
calcolato lungo la trasformazione
(1), mentre il secondo lungo la
trasformazione (2).
Siccome il ciclo è reversibile, la
trasformazione (2) si può
eseguire in verso opposto (da A a B).
Quindi:

B
A
dS 
(1)

B
A
dS  0
(2)
da cui:
B
B
A
A
 dS  
(1)
dS
(2)
Stante la completa generalità delle due trasformazioni,
l’equazione precedente prova che l’integrale di dS, calcolato
tra due stati di equilibrio, ha lo stesso valore per tutte le
trasformazioni (reversibili) che collegano quei due stati.
c.v.d.
La variazione di entropia tra due stati A e B è allora:
B
B
A
A
S  S B  S A   dS  
dQ
T
(21)
dove l’integrale è calcolato lungo una qualsiasi
trasformazione reversibile che collega i due stati.
Nel SI l’unità di misura dell’entropia è J/K.
Oltre all’entropia, altre funzioni di stato sono l’energia
potenziale, l’energia interna, la pressione, la temperatura ed
altre ancora. Il calore ed il lavoro non sono funzioni di stato.
In termodinamica si preferisce il termine parametro di stato o
coordinata termodinamica per indicare una funzione di stato.
Se lo stato di un sistema termodinamico è descrivibile
mediante due soli parametri di stato (come ad esempio un
gas), è spesso utile descriverlo tramite i parametri di stato S e
T.
Il diagramma S-T con cui si può rappresentare una
trasformazione di un tale sistema viene detto diagramma
entropico.
Ricordando la (20):
dQ = T dS
da cui, integrando:
QAB 

B
A
B
dQ   T dS
A
Nel diagramma entropico l’area sotto la curva che
rappresenta graficamente la trasformazione (reversibile) è
pari alla quantità di calore scambiata nella trasformazione.
In particolare un ciclo di Carnot viene rappresentato in modo
molto semplice nel diagramma entropico.
(a)
(b)
Dal riquadro (b) della figura si vede subito che il calore netto
assorbito durante il ciclo vale:
Q  Q1  Q3  ( S B  S A ) (T1  T2 )
D’altra parte:
Q1  T1 ( S B  S A )
Pertanto:
e 
L
Q
( S  S A ) (T1  T2 )
T

 B
1 2
Q1
Q1
T1 ( S B  S A )
T1
Entropia di un corpo solido
Per la (20) e per la definizione di calore specifico:
dS  m c
dT
T
dove m è la massa del corpo e c il suo calore specifico.
Questa equazione permette di valutare la variazione S di
entropia in una qualunque trasformazione reversibile fra uno
stato di riferimento R arbitrariamente scelto (di temperatura
TR) ed un generico stato P (di temperatura T ).
Integrando tra questi due stati otteniamo:
T
S  m  c
TR
dT
T
Supponiamo di attribuire allo stato di riferimento un’entropia
di valore arbitrario pari a SR. Assumendo inoltre un valore del
calore specifico indipendente dalla temperatura, si ricava:
S  S R  m c ln (
T
)
TR
In definitiva l’entropia di un solido di massa m e calore
specifico c, posto a temperatura T, è data da:
S  m c ln (
T
)  SR
TR
Entropia di un gas perfetto
Ricordando la forma differenziale del primo principio, la (20)
si può scrivere come:
dS 
dQ dEint  dL

T
T
(22)
Ma:
dEint  n cV dT
dL   p dV  
n RT
dV
V
Sostituendo nella (22), si ricava:
dS  n cV
dT
dV
 nR
T
V
Tramite questa equazione si può calcolare, come prima, la
variazione S di entropia in una trasformazione reversibile fra
uno stato di riferimento R arbitrariamente scelto (di
coordinate termodinamiche TR e VR) ed un generico stato P (di
coordinate T e V).
Integrando tra questi due stati otteniamo:
T
S  n  cV
TR
V dV
dT
 nR
VR V
T
Come prima supponiamo di attribuire allo stato di riferimento
un’entropia di valore arbitrario pari a SR. Assumendo inoltre
un valore del calore specifico indipendente dalla temperatura,
si ricava:
S  S R  n cV ln (
T
V
)  n R ln ( )
TR
VR
da cui:
S  n cV ln (
T
V
)  n R ln ( )  S R
TR
VR