Il trasformatore

Il trasformatore
FUNZIONAMENTO IN REGIME ALTERNATO SINUSOIDALE
In presenza di una alimentazione alternata sinusoidale tutte le grandezze
elettriche saranno alternate sinusoidali.
Le equazioni di funzionamento in regime comunque variabile diventano le
equazioni di regime alternato sinusoidale sostituendo ai valori istantanei le
grandezze vettoriali e alle derivate il termine jω.
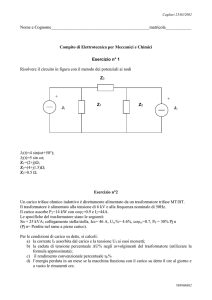
V1 = R 1 I1 + jX l1 I1 + jX m I 0 = Z 1 I1 + E 1
V 2 = R 2 I2 + jX l 2
I2 + E 2 = Z 2 I2 + E 2
24
Il trasformatore
I1
V1
I’2
Z1
Z2
I0
R0
Xm
E1
E2
I2
V2
Si introduce una resistenza R0 in parallelo a Xm che tiene conto delle perdite nel
ferro (le perdite nel ferro dipendono dal flusso e il flusso dipende dalla tensione ai
capi di Xm).
Per i diversi funzionamenti (a vuoto, in corto circuito, a carico) è sempre possibile
costruire dei diagrammi vettoriali di funzionamento.
25
Il trasformatore
CIRCUITI EQUIVALENTI RIDOTTI
Per lo studio di particolari condizioni di funzionamento è conveniente utilizzare
dei circuiti equivalenti ridotti ottenuti trasferendo le impedenze da una parte
all’altra del trasformatore ideale.
Il trasferimento avviene sulla base della costanza della potenza.
ia
ib
ea
Na
Nb
Relazioni valide per il trasformatore ideale:
eb
ea
Na
ib
1
=
=
=
eb
Nb
ia
k
26
Il trasformatore
TRASFORMAZIONI A POTENZA COSTANTE:
Rb
ia
R’b
ib
ea
eb
R b i 2b = R ' b i a2
 ib
R ' b = R b 
 ia
Lb
ia
ea
X
2
bib



2
 Na 

= R b 
 Nb 
2
Rb
=
k2
L’b
ib
eb
=
X ' b i a2
 ib
X ' b = X b 
 ia



2
 Na 

= X b 
 Nb 
2
=
Xb
k2
27
Il trasformatore
L’impedenza vista dai morsetti di alimentazione nel funzionamento in corto
circuito è:
Z1
Z’2
Z cc = Z 1 +
Poiché
Z '2 ∗ Z 0
Z '2 + Z 0
Z0
Z ' 2 << Z 0
Z ' cc ≅ Z 1 + Z ' 2
Z1
Z’2
Zcc è l’IMPEDENZA DI CORTO CIRCUITO DEL TRASFORMATORE
28
Il trasformatore
Altri possibili circuiti equivalenti sono i seguenti:
Z1
Z’2
con approssimazione
Z0
Z1
Z’2
con approssimazione
Z0
Z’1
Z2
Z0
29
Il trasformatore
POTENZA NOMINALE DI UN TRASFORMATORE
Per giungere alla definizione della potenza nominale, si noti che:
• le perdite nel trasformatore sono funzione del flusso (e quindi della f.e.m. E)
(PERDITE NEL FERRO) e della corrente (PERDITE NEL RAME).
• il rapporto tra le tensioni primaria e secondaria è definito in modo univoco solo
a vuoto.
• si introduce la TENSIONE NOMINALE DEL PRIMARIO (avvolgimento
alimentato) V1n e si deduce la tensione nominale secondaria V2n (avvolgimento
su cui è collegato il carico) come tensione secondaria a vuoto V20.
Risulta:
V 20
V2n
=
= k
V1 n
V1 n
30
Il trasformatore
POTENZA NOMINALE DI UN TRASFORMATORE
• si introduce la CORRENTE NOMINALE SECONDARIA (avvolgimento
chiuso sul carico) I2n e si deduce la corrente nominale primaria I1n mediante il
rapporto spire (relazione valida solo in corto circuito).
Risulta:
I1n
= k
I 2n
V 20
V2n
I1n
=
=
= k
V1 n
V1 n
I 2n
V 2 n I 2 n = V 20 I 2 n = V1 n I 1 n
31
Il trasformatore
POTENZA NOMINALE DI UN TRASFORMATORE
Si definisce POTENZA NOMINALE DI UN TRASFORMATORE (potenza
resa al secondario espressa in [VA]) il prodotto della corrente secondaria
nominale I2n per la tensione secondaria a vuoto (V20= V2n ).
Per la relazione già introdotta tra le grandezze primarie e secondarie risulta
inoltre:
A n = V 2 n I 2 n = V1 n I 1 n
e cioè le potenze nominali primarie e secondarie sono uguali.
32
Il trasformatore
TRASFORMATORI TRIFASE
L’esistenza di linee di trasmissione di energia elettrica trifase imporrebbe la
presenza di 3 trasformatori monofase ogni qualvolta si intendesse realizzare una
trasformazione delle grandezze elettriche tensione e corrente.
In questo caso si giungerebbe ad un sistema del tipo indicato in figura (si
suppone un collegamento a ∆ e di essere in regime alternato sinusoidale).
33
Il trasformatore
1
2
3
Φ1
v12
Φ2
Φ3
v23
v31
1
2
3
V12 + V 23 + V 31 = 0
34
Il trasformatore
Nell’ipotesi di trascurare le cadute di tensione nei circuiti equivalenti risulta:
V12 ≅ E 12
si associa
Φ 01
V 23 ≅ E 23
si associa
Φ 02
V 31 ≅ E 31
si associa
Φ 03
Φ 01 + Φ 02 + Φ 03 = 0
Sfruttando la relazione precedente si può arrivare ad una semplificazione
costruttiva:
Φ 01 + Φ 02 + Φ 03 = 0
35
Il trasformatore
Nella colonna centrale circola un flusso risultante nullo e quindi la colonna
centrale comune ai tre trasformatori può essere eliminata.
N.B.: Ciò è vero se il sistema di tensioni è simmetrico, se i tre trasformatori
sono uguali e se il carico è ripartito in modo uniforme sulle tre fasi.
Se il carico è squilibrato, le cadute di tensione sono diverse, così pure le E, e
quindi la loro somma (e quella dei flussi) non è più nulla.
Esiste quindi una differenza di potenziale magnetico ∆U tra il nodo superiore e
quello inferiore.
La stessa cosa accade se, a pari flusso, le riluttanze dei tronchi di circuito
magnetico sono diverse tra loro.
36
Il trasformatore
Con ∆U ≠ 0 ci sarà un flusso in aria tra il nodo superiore e quello inferiore pari
alla somma dei tre flussi:
Φ a = Φ 01 + Φ 02 + Φ 03
Tale flusso è generalmente piccolo perché la riluttanza del tronco in aria è
elevata.
In pratica si utilizzano circuiti magnetici a 3 colonne:
b.t.
A.T.
N.B.: Esistono anche trasformatori speciali a 5 colonne.
37
Il trasformatore
EQUAZIONI DI FUNZIONAMENTO DEI
TRASFORMATORI TRIFASE
Ipotesi: si trascurano le mutue tra avvolgimenti di fasi diverse, in quanto si è
supposto nullo il flusso nella colonna centrale.
 ψ 1   L1
 Ψ  M
 1*   1* 1
 ψ2   0

 = 
Ψ 2*   0
 ψ3   0

 
 Ψ 3 *   0
ove:
M 11 *
L 1*
0
0
0
0
0
0
L2
M 2* 2
0
0
0
0
M 22 *
L 2*
0
0
0
0
0
0
L3
M 3* 3
  i1 
i 
  1* 
 i2 


 i 2 * 
M 33 *   i 3 


L 3 *   i 3 * 
0
0
0
0
1
1*
avvolgimento primario e secondario della fase 1
2
2*
avvolgimento primario e secondario della fase 2
3
3*
avvolgimento primario e secondario della fase 3
38
Il trasformatore
EQUAZIONI DI FUNZIONAMENTO DEI TRASFORMATORI TRIFASE
M11*
mutua tra l’avvolgimento primario e quello secondario della fase 1
Lo studio di un trasformatore trifase si riconduce quindi a quello di un sistema
di tre trasformatori monofasi indipendenti (per ciascuno dei quali vale il circuito
equivalente già introdotto).
Ogni fase è indipendente e il suo comportamento è uguale a quello delle altre
fasi con forzanti sfasate di 2π/3 nel tempo.
39
Il trasformatore
COLLEGAMENTI TRA AVVOLGIMENTI DI FASE NEI
TRASFORMATORI TRIFASE
Gli avvolgimenti di fase possono essere collegati tra di loro a stella o a
triangolo.
Si indica generalmente con la maiuscola l’A.T. e con la minuscola la b.t.:
A.T.
D
Y
b.t.
d
y
Esempi di collegamenti:
stella-stella
Y
y
triangolo-triangolo
D
d
COLLEGAMENTI OMONIMI
triangolo-stella
D
y
stella-triangolo
Y
d
COLLEGAMENTI ETERONIMI
40
Il trasformatore
Si definisce:
RAPPORTO DI TRASFORMAZIONE KT =
=
ten sio n e co n caten ata a vu o to S E C O N D A R IA
ten sio n e co n caten ata a vu o to P R IM A R IA
RAPPORTO SPIRE KS
=
sp ire avvo lg im en to S E C O N D A R IO
sp ire avvo lg im en to P R IM A R IO
=
f.e.m . d i fase S E C O N D A R IA
f.e.m . d i fase P R IM A R IA
Risulta:
KT = KS
per collegamenti OMONIMI
KT =
per collegamenti
Y
d
per collegamenti
D
y
KT =
3K S
KS
3
41
Il trasformatore
SFASAMENTI - INDICE ORARIO
Le tensioni primarie e secondarie, oltre che differire in valore numerico,
risultano anche sfasate tra di loro.
L’entità dello sfasamento dipende dal tipo di collegamento.
Per definire lo sfasamento si introduce il GRUPPO o INDICE ORARIO.
L’unità base (v. norme CEI) è lo sfasamento di 30° (uno sfasamento di 180°
corrisponde a un indice orario 6).
42
Il trasformatore
SFASAMENTI - INDICE ORARIO
Per valutare l’indice orario si procede nel seguente modo:
• si considera una circonferenza suddivisa in archi di π/6 e numerata come il
quadrante di un orologio;
• si dispone il vettore di tensione di fase PRIMARIA sulla posizione 0
(equivalente alle ore 12);
• si dispone il vettore di tensione di fase SECONDARIA riferita al centro della
stella reale (collegamento a stella) o teorico (baricentro del triangolo delle tensioni
concatenate nel caso di collegamento a triangolo);
0
1
11
• l’indice orario si identifica con l’ora su cui
10
2
è puntato il vettore di tensione di fase
vf
SECONDARIA.
9
3
Esempio: INDICE ORARIO 6
v*f
8
4
7
5
6
42
Il trasformatore
SFASAMENTI - INDICE ORARIO
Si noti che:
• a collegamenti OMONIMI corrispondono indici orari PARI;
• a collegamenti ETERONIMI corrispondono indici orari DISPARI.
Esempi:
1
2
3
A.T.
1
2
3
A.T.
1’ 2’ 3’
b.t.
b.t.
1’ 2’ 3’
Y y 0
Y y 6
43
Il trasformatore
SFASAMENTI - INDICE ORARIO
Esempi:
1
2
3
A.T.
1
Y
A.T.
3
1’
b.t.
2’
3’
2
1’
b.t.
d
3’
2’
Y d 11
44
Il trasformatore
SFASAMENTI - INDICE ORARIO
Esempi:
vf1
1’
v1’3’
3’
vf3
vf1
v2’1’
v*f1
11
2’
v*f1
v3’2’
vf2
Y d 11
45