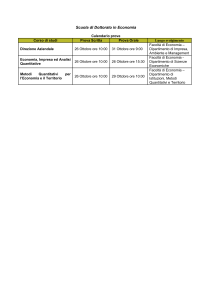
Elementi di statistica per l’analisi
dei materiali archeologici
Julie Arnaud
[email protected]
https://perso.univ-rennes1.fr/denis.poinsot/Statistiques_%20pour_statophobes/STATISTIQUES%20POUR%20STATOPHOBES.pdf
Statistica – Perché?
Popolazione
Statistica
Stima
Test
Campionamento
Probabilità
Campione
Osservazione
Variabile
Statistica – Perché?
Population
Statistics
estimation
Test
Sampling
Probability
Sample
Observation
Variable
Statistica – Perché?
• Due medie o due proporzioni saranno SEMPRE differente tra di loro
• Almeno una parte di questa differenza sarà dovuta al caso dovuto alle
fluttuazione di campionamento
=> È dunque indispensabile (per evitare di arrivare a conclusioni sbagliate) di
stimare l’affidabilità dei dati (intervallo di confidenza) e eventualmente di
calcolare la probabilità che una differenza cosi grande possa essere osservata
semplicemente per via della casualità (test statistici)
La statistica è l’unico modo di verificare di maniere obbiettiva e
riproducibile da chiunque i vostri risultati e conclusioni.
Statistics – why?
• Two mean or two percentage will ALWAYS be different between them
• At least part of this difference will be unpredictable because of the
sampling fluctuations.
It is then necessary (to avoid wrong conclusion) to estimate the reliability
of the data (confidence interval) and eventually to calculate the probability
that this important difference is due to the randomness (statistic test).
Statistics are the only way to check impartially your
results and your conclusion
Cos'è una variabile casuale?
Una variabile è una caratteristica studiata per una popolazione data.
Casuale perché teoricamente non si può sapere in anticipo il risultato.
A variable is a features studied for a given population
Random because theoritically we don’t know the results in advance.
Individui
1
…
i
…
n
1
x11
…
…
Variabili
j
x1j
…
xi1
…
…
…
xij
…
xn1
…
xnj
…
…
p
x1p
…
…
xip
…
…
xnp
Cos’è una variabile casuale?
Tipi di variabili
Qualitative
Nominale
Ex:
Nome
Colori
Sesso
Stagione
Professione
Ordinale
Ex:
Voti (A, B,
etc.)
Grado di
soddisfazione
Quantitative
Discrete
Ex:
Età
Numero di
bambini
Come calcolare la media dei nomi o dei colori?
Continue
Ex:
Taglia
Peso
Lunghezza
Larghezza
Cos’è una variabile casuale?
Variabili qualitative (categorie) = visibili senza essere misurate
Qualitative variables (categories) = visible without measurements
- Nominali: colori, nomi, sesso
- Ordinali: molto insoddisfatto, insoddisfatto, neutro, soddisfatto, molto
soddisfatto
Variabili quantitative (numeriche)
Quantitative variables (numerical)
- Discreti: Numeri interi naturali: età, numero di abitanti, numero di bambini…
- Continui: Temperature, distanze, tutti tipi di misure
Definizione…
«La distribuzione normale è una distribuzione di probabilità continua che è spesso usata
come prima approssimazione per descrivere variabili casuali a valori reali che tendono a
concentrarsi attorno ad un singolo valor medio. Il grafico della funzione di densità di
probabilità associata è simmetrico e ha una forma a campana, nota come campana di Gauss.
La distribuzione normale è considerata il caso base delle distribuzioni di probabilità continue a
causa del suo ruolo nel teorema del limite centrale. Più specificamente, assumendo certe
condizioni, la somma di n variabili casuali con media e varianza finite tende a una
distribuzione normale al tendere di n all'infinito» (Wikipedia).
Definition…
The normal distribution is a very common continuous probability distribution. Normal
distributions are important in statistics and are often used in the natural and social
sciences to represent real-valued random variables whose distributions are not known. The
normal distribution is useful because of the central limit theorem. In its most general form,
under some conditions (which include finite variance), it states that averages of random
variables independently drawn from independent distributions converge in distribution to
the normal, that is, become normally distributed when the number of random variables is
sufficiently large.
Campionamento
Analisi del
campione
Statistiche descrittive
Popolazione
Inferenza statistica:
Affermazione riguardando la
popolazione sulla base del
campione
Sampling
Sample
analysis
Descriptive statistics
Population
Statistic inference:
Statement on the population
based on the sample
Campionamento
Il campione non è una popolazione / The sample is not a population
- Unità/Unit = un oggetto di studio / object of study
- Una popolazione/Population = insieme di unità / set of units
L’effettivo di una popolazione può essere proibitivo (ex: il numero di pesce nel mare).
The population size can be prohibitive (ex: number of fish in the sea)
Bisogna quindi scegliere un sotto-insieme / Necessity to choose a subset
- Campione/sample = sotto-insieme di una popolazione / subset of a
population
Ma l’informazione contenuta in un campione è incompleta, e quindi favorisce i errori
(Esempio sondaggio telefonico).
The information included in the sample is incomplet which can bring mistake.
Campionamento
Il campione non è una popolazione
Tipi di campionamento
Campionamento a random / Random sampling
Prelevare a caso e di maniera indipendente n unità di campionamento di una
popolazione statistica di N elementi. Ogni unità di campionamento deve avere la
stessa probabilità che gli altri di essere pescata.
Collect randomly and independently n unit of sampling in a statistical population
of N elements. Each Unit of sampling has to have the same probability than the
other to be collected.
Probabilità = numero di caso favorevole / numero di casi possibili
Ex: dado: probabilità (1) =
Tipi di campionamento
Campionamento a random
Prelevare a caso e di maniera indipendente n unità di campionamento di una
popolazione statistica di N elementi. Ogni unità di campionamento deve avere la
stessa probabilità che gli altri di essere pescata.
Collect randomly and independently n unit of sampling in a statistical population
of N elements. Each Unit of sampling has to have the same probability than the
other to be collected.
Probabilità = numero di caso favorevole / numero di casi possibili
Ex: dado: probabilità (1) = 1/6 (casi possibili)
Ex: una busta con tre palline: 1 bianca e 2 rosse
Proba (bianca) = ?
Proba (rossa) = ?
Tipi di campionamento
Campionamento a random
Prelevare a caso e di maniera indipendente n unità di campionamento di una
popolazione statistiche di N elementi. Ogni unità di campionamento deve avere la
stessa probabilità che li altri di essere pescata.
Collect randomly and independently n unit of sampling in a statistical population
of N elements. Each Unit of sampling has to have the same probability than the
other to be collected.
Probabilità = numero di caso favorevole / numero di casi possibili
Ex: dado: probabilità (1) = 1/6 (casi possibili)
Ex: una busta con tre palline: 1 bianca e 2 rosse
Proba (bianca) = 1/3
Proba (rossa) = 2/3
Tipi di campionamento
Campionamento sistematico / Sistematic sampling
Prelevare a caso il primo elemento di una serie di unità di campionamento, poi
prelevare tutti i seguenti con un intervallo conosciuto in anticipo.
Collect randomly the first elements of a serie of sampling unit, then collect all the
other with a given interval.
Le unità di campionamento non sono quindi prelevate in modo indipendente
Sampling units are not collected independenlty
Ex: una lista di persone, la prima è scelta a random tra i 20 primi nomi poi
regolarmente tutti i 20 nomi (n°7, 27, 47, etc..)
Errori
- Errori di campionamento : il campione non è una popolazione
- Errori di misure
Quanti elementi in un campione?
Un campione è statisticamente corretto quando si tratta di 30 o più individui, perché?
A sample is statisticly correct when the number of individual is more than 30, why?
Quanti elementi in un campione?
Un campione è statisticamente corretto quando si tratta di 30 o più individui, perché?
A sample is statisticly correct when the number of individual is more than 30, why?
Una media segue una distribuzione approssimativamente normale quando è
stabilità a partire da un campione composta da un infinito numero di individui….
A mean follows an approximatively normal distribution when calculated from a
sample composed of an infinit number of individuals…
Quanti elementi in un campione?
Un campione è statisticamente corretto quando si tratta di 30 o più individui, perché?
A sample is statisticly correct when the number of individual is more than 30, why?
Una media segue una distribuzione approssimativamente normale quando è
stabilità a partire da un campione composta da un infinito numero di individui….
A mean follows an approximatively normal distribution when calculated from a
sample composed of an infinit number of individuals…
In statistica, l’infinito inizia a 30!!!
In statistics, infinite start at 30!!!
Campionamento
Analisi del
campione
Statistiche descrittive
Popolazione
Inferenza statistica:
Affermazione riguardando la
popolazione sulla base del
campione
Come presentare i dati?
Statistiche descrittive:
Tecniche che permettono di presentare, descrivere e riassumere un insieme di dati
1° tappa: Stabilire la strutture dei dati
- assegnare i nomi e tipi di variabili
- Decidere una codificazione dei variabili
2° tappa: La matrice (tabella) dei dati
- Produrre la matrice dei dati
- Controllare la matrice per scoprire eventuali errori
3° tappa: Tabelle di frequenza (dati qualitativi)
4° tappa: Rappresentazione grafica (se necessaria)
5° tappa: Calcolo di parametri di distribuzione (solo per dati quantitativi)
How to present the data?
Descriptive statistics:
Technics which allow to present, describe and summarize the data.
1° step: Establish the structure of the data
- Assign names and type of variables
- Decide the codification of the variables
2° step: Matrix (table) of data
- Build the matrix
- Control the matrix to highlight errors
3° tappa: Frequence tables (qualitative data)
4° tappa: Graphic representation (if necessary)
5° tappa: Calculate distribution parameters (only of quantitative data)
Come presentare i dati?
Statistiche descrittive:
Tecniche che permettono di presentare, descrivere e riassumere un insieme di dati
1° tappa: Stabilire la strutture dei dati
- assegnare i nomi e tipi di variabili
- Decidere una codificazione dei variabili
2° tappa: La matrice (tabella) dei dati
- Produrre la matrice dei dati
- Controllare la matrice per scoprire eventuali errori
3° tappa: Tabelle di frequenza (dati qualitativi)
4° tappa: Rappresentazione grafica (se necessaria)
5° tappa: Calcolo di parametri di distribuzione (solo per dati quantitativi)
Cane
Colore
Sesso
Taglia (m)
1
NB
M
0.15
2
NB
F
0.6
3
B
M
0.2
4
NB
C
0.2
5
M
M
1
6
B
F
0.35
7
M
M
2.8
8
Verde
F
0.12
9
NB
F
0.35
Cane
Colore
Sesso
Taglia (m)
1
NB
M
0.15
2
NB
F
0.6
3
B
M
0.2
4
NB
M
0.2
5
M
M
1
6
B
F
0.35
7
M
M
0.8
8
M
F
0.12
9
NB
F
0.35
Come presentare i dati?
Statistiche descrittive:
Tecniche che permettono di presentare, descrivere e riassumere un insieme di dati
1° tappa: Stabilire la strutture dei dati
- assegnare i nomi e tipi di variabili
- Decidere una codificazione dei variabili
2° tappa: La matrice (tabella) dei dati
- Produrre la matrice dei dati
- Controllare la matrice per scoprire eventuali errori
3° tappa: Tabelle di frequenza (dati qualitativi)
4° tappa: Rappresentazione grafica (se necessaria)
5° tappa: Calcolo di parametri di distribuzione (solo per dati quantitativi)
Tabella degli effettivi
Colori
Effettivi
Sesso
Effettivi
NB
4
M
5
B
2
F
4
M
3
Totale
9
Totale
9
Sesso
Colori
M
F
NB
2
2
B
1
1
M
2
1
Totale= 9
Tabella delle frequenza e percentuale
Frequenza = effettivi della classe / Effettivi totali
Percentuale = frequenza X 100
Colori
Frequenza
NB
4/9 = 0.44
B
2/9 = 0.22
M
3/9 = 0.33
Sesso
Frequenza
M
5/9 = 0.55
F
4/9 = 0.44
Sesso
Colori
M
F
NB
2/9 = 0.22
2/9 = 0.22
B
1/9 = 0.11
1/9 = 0.11
M
2/9= 0.22
1/9= 0.11
Totale= 1
Come presentare i dati?
Statistiche descrittive:
Tecniche che permettono di presentare, descrivere e riassumere un insieme di dati
1° tappa: Stabilire la strutture dei dati
- assegnare i nomi e tipi di variabili
- Decidere una codificazione dei variabili
2° tappa: La matrice (tabella) dei dati
- Produrre la matrice dei dati
- Controllare la matrice per scoprire eventuali errori
3° tappa: Tabelle di frequenza (dati qualitativi)
4° tappa: Rappresentazione grafica (se necessaria)
5° tapa: Calcolo di parametri di distribuzione (solo per dati quantitativi)
Rappresentazione grafica (variabili qualitative e quantitative discrete)
Diagrammi a Barre
Rappresentazione grafica (variabili qualitative e quantitative discrete)
Diagrammi a torte
Rappresentazione grafica (variabili qualitative e quantitative discrete)
Combinazione dei due
Rappresentazione grafica (variabili quantitative continue)
Istogrammi
Stabilire delle classe
Come presentare i dati?
Statistiche descrittive:
Tecniche che permettono di presentare, descrivere e riassumere un insieme di dati
1° tappa: Stabilire la strutture dei dati
- assegnare i nomi e tipi di variabili
- Decidere una codificazione dei variabili
2° tappa: La matrice (tabella) dei dati
- Produrre la matrice dei dati
- Controllare la matrice per scoprire eventuali errori
3° tappa: Tabelle di frequenza (dati qualitativi)
4° tappa: Rappresentazione grafica (se necessaria)
5° tappa: Calcolo di parametri di distribuzione (solo per dati quantitativi)
Parametri di distribuzione : Misura di posizione
Media / Mean
Il valore ottenuto sommando tutti i dati e dividendo questa somma con il
numero di dati
Mediana / Median
Valore smezzando la distribuzione in due parte con lo stesso effettivo
Per un numero dispari di dati
Per un numero pari di dati
Moda / Mode
Corrisponde al valore il più rappresentato di una variabile (frequenza massima) di
un campione. Una ripartizione può essere plurimodale se ci sono diverse valore
emergente (taglia maschio/femmina)
Ripartizione plurimodale
Parametri di distribuzione : Misura di posizione
0.5
0.6
0.7
Indice de robustesse au FM (Epaisseur/Hauteur)
0.4
Gua II
0.3
Gua III
HN
HS
MPL
Parametri di distribuzione : Misura di posizione
Outsiders
Massimo
Q75
50 % dei
valori
Q50 = Mediana
Q25
Minimo
Parametri di distribuzione : Misura di posizione
Parametri di distribuzione : Criteri di dispersione
Scelta per le vacanze:
1° possibilità: La Datcha del corvo morto,
una pensiona familiare tranquilla nella
periferia industriale di Verkoïansk (Siberia)
Età media dei 252 ospite = 64 anni*
2° possibilità: Surf island, un isola paradisiaca
Età media dei 248 ospite = 22 anni**
Note:
*varianza = 1225 anni (quadrati)
**varianza = 1209 anni (quadrati)
Parametri di distribuzione : Criteri di dispersione
Scelte per le vacanze:
1° possibilità: La Datcha del corvo morto,
una pensiona familiare tranquilla nella
periferia industriale di Verkoïansk (Siberia)
Età media dei 252 ospite = 64 anni*
2° possibilità: Surf island, un isola paradisiaca
Età media dei 248 ospite = 22 anni**
Note:
*varianza = 1225 anni²
**varianza = 1209 anni²
Parametri di distribuzione : Criteri di dispersione
Scelte per le vacanze:
1° possibilità:
2° possibilità:
Parametri di distribuzione : Criteri di dispersione
Il peso medio dei mammiferi adulti è di circa 1 kg….
2g
150 tonnellate
Parametri di distribuzione : Criteri di dispersione
La media deve SEMPRE essere accompagnata di almeno un parametro di dispersione /
Mean should ALWAYS go with at least one dispersion parameter :
In generale si usa la varianza/deviazione standard : la differenza alla media
Generaly we use variance/standard deviation: the difference to the mean
Esempio di due campioni
che hanno la stessa
media ma due deviazione
standard differenti
Parametri di distribuzione : Criteri di dispersione
La media deve SEMPRE essere accompagnata di almeno un parametro di dispersione /
Mean should ALWAYS go with at least one dispersion parameter :
In generale si usa la varianza/deviazione standard : la differenza alla media
Generaly we use variance/standard deviation: the difference to the mean
Varianza(σ2) = media dei quadrati dei scarti alla media / mean of the squared
differences from the mean
Deviazione standard (σ) = radice quadrata della varianza
Corrisponde alla dispersione dei dati attorno alla media della popolazione
campionata. Stessa unità della variabile.
The standard deviation is the dispersion of the data around the mean of the
population. Same unit than the variable.
Parametri di distribuzione : Criteri di dispersione
L’errore standard della media (diversa della deviazione standard dei dati) / Standard error
of the mean (different from the standard deviation of the data)
e.s = √(𝜎^2/𝑛)
- Dipende dal numero n di dati nel campione -> più il campione è grande più l’errore
standard è piccola. / Dipends on the number n of data in the sample : larger is the
sample, smalle is the standard error
- Traduce quindi la precisione della stima della media / the precision of the estimation of
the mean
Parametri di distribuzione : Criteri di dispersione
Esempio
Valore del campione: 1, 2, 3, 6
Effettivi: n = 4
Media: m = 3
Somma dei quadrati delle deviazione alla media (SQD)
(1-3)² + (2-3)² + (3-3)² + (6-3)² = 14
Varianza del campione : SQD/n = 14/4 = 3,5
Deviazione standard del campione: 3,5= 1,871
Varianza stimata della popolazione: s²= SQD/(n-1) = 14/3 = 4,667
Deviazione standard della popolazione: s= √4,667 = 2,160
Errore standard della media: e.s. =√(s²/n) = √(4,667/4)
Si può quindi scrivere: m = 3 ± 1,08
Parametri di distribuzione : Criteri di dispersione
Anche le percentuali hanno un errore standard!
e.s =√ (p(1-p) / (n – 1))
Esempio
Frequenza osservata di p = 0,20 su 50 individui
e.s. = √(0,20 × 0,8 / 49) = 0,057
Si può scrivere: p = 0,20 ± 0,057 o p = 20 ± 5,7%
L’Intervallo di Confidenza
Fino a quando ci possiamo fidare delle valore stimate a partire di un campione?
How can we trust the estimated value from a sample?
L’intervallo di confidenza rappresenta la zone in cui si trova « molto probabilmente » (con
una probabilità che si sceglie, generalmente 0,95 o 0,99), il vero valore del parametro che
stiamo studiando in una popolazione.
The confidence interval represents the area where we can find «most probably» (with a
probability of 0,95 or 0,99), the true value of the parameter studied in a population.
𝜇 = 𝑚 ± 1,96 𝑠 2 /𝑛
L’Intervallo di Confidenza
Fino a quando ci possiamo fidare delle valore stimate a partire di un campione?
How can we trust the estimated value from a sample?
L’intervallo di confidenza rappresenta la zone in cui si trova « molto probabilmente » (con
una probabilità che si sceglie, generalmente 0,95 o 0,99), il vero valore del parametro che
stiamo studiando in una popolazione.
The confidence interval represents the area where we can find «most probably» (with a
probability of 0,95 or 0,99), the true value of the parameter studied in a population.
𝜇 = 𝑚 ± 1,96 𝑠 2 /𝑛
𝜇 = il vero valore
m = media
s² = Varianza
n = effettivi
Et 1,96???
L’Intervallo di Confidenza
Condizione:
- Grande campione (n>30) / Large sample (n>30)
- La variabile random segue una distribuzione normale / The variable follows a
normal distribution
Quando si tratta di un campione di più di 30 individui, la media segue una legge
approssimativamente normale / When the size of the sample is more than 30,
the mean follows approximatly a normal distribution
95 % delle valore
si trovano a 1,96
errore standard
attorno alla media
L’Intervallo di Confidenza
Fino a quando ci possiamo fidare delle valore stimate a partire di un campione?
L’intervallo di confidenza rappresenta la zone in cui si trova « molto probabilmente » (con
una probabilità che si sceglie, generalmente 0,95 o 0,99), il vero valore del parametro che
stiamo studiando in una popolazione.
𝜇 = 𝑚 ± 1,96 𝑠 2 /𝑛
Esempio:
Media osservata: m = 178,025 cm
Varianza stimata: s² = 50,384
e.s. = 𝑠 2 /𝑛 = √(50,384 / 40) = 1,122 cm
Limite inferiore della soglia à 95%: 178,025 – 1,96 × 1,122 = 175,8 cm
Limite superiore della soglia a 95%: 178,025 + 1,96 × 1,122 = 180,2 cm
IC95% = [175,8 − 180,2 cm]
Riassunto: presentazione delle variabili
Tabella degli effettivi o
delle frequenze
Dati qualitativi o
quantitativi discreti
Dati quantitativi
continui
Raggruppamento
per classe
(intervallo di valore)
Dati qualitativi o
quantitativi discreti
Diagrammi a
barra/torte
Dati quantitativi
continui
Istogramma
Boxplot
Dati univariati
Rappresentazione grafiche
Non dimenticare di accompagnare i grafici degli effettivi e dei criteri di dispersione
Riassunto: Esempio di dati quantitativi continui
Precipitazione annuali di una città americana
Misure di
tendenze centrale
Misure di
posizione
Localizzare i dati nel
loro insieme sull’asse
dei valori delle variabili
Separare i dati in due o
diversi gruppo distinti
e ordinati
Media
Mediana
Mediana
Quartile
Valori minimali e massimali
Misure di
dispersione
Definisce lo
spandimento dei dati
su un asso stesso
Variazione
Deviazione standard
Riassunto: Esempio di dati quantitativi continui
Riassunto: Esempio di dati quantitativi continui
Esempio di distribuzione che presentano la stessa media ma delle dispersione diverse
Riassunto: Esempio di dati quantitativi continui
Riassunto: Esempio di dati quantitativi continui
Raggruppamento per classe
Dati bivarianti
Quanto si tratta di confrontare due variabili, si usa generalmente delle nuvole di punti
Esempio: Misure su 50 granchi per colore (blu e arancione) e sesso, della specie
Leptograpsus variegatus.
Dati bivarianti
Dati bivarianti
Dati bivariati
Dati bivarianti
Software
SPSS
Freeware
https://www.r-project.org/
PAST http://folk.uio.no/ohammer/past/