Elettrotecnica - A.A. 2011-12 - Prova n. 2 – 27 gennaio 2012
Cognome
Parti svolte:
Nome
E1
E2
Matricola
Firma
1
D
Esercizio 1
A
R1
VG1
R2
R3
C
B
D
R4
IG6
R7
rI2
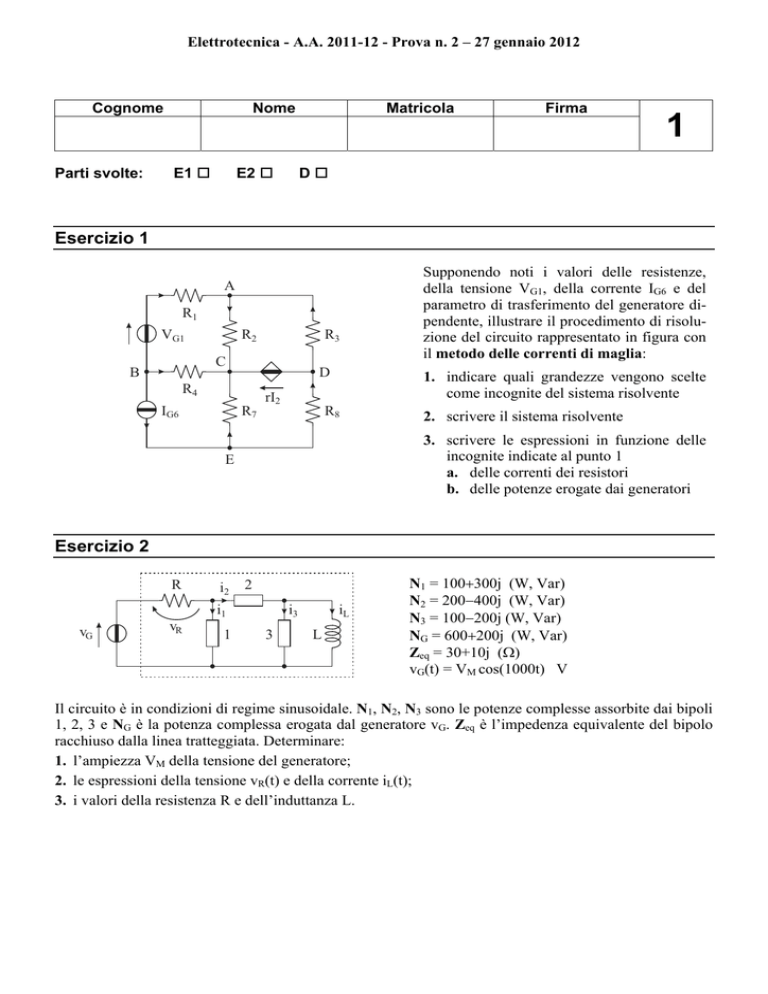
Supponendo noti i valori delle resistenze,
della tensione VG1, della corrente IG6 e del
parametro di trasferimento del generatore dipendente, illustrare il procedimento di risoluzione del circuito rappresentato in figura con
il metodo delle correnti di maglia:
1. indicare quali grandezze vengono scelte
come incognite del sistema risolvente
R8
2. scrivere il sistema risolvente
3. scrivere le espressioni in funzione delle
incognite indicate al punto 1
a. delle correnti dei resistori
b. delle potenze erogate dai generatori
E
Esercizio 2
R
vG
vR
i2
2
i1
1
i3
3
iL
L
N1 = 100300j (W, Var)
N2 = 200400j (W, Var)
N3 = 100200j (W, Var)
NG = 600200j (W, Var)
Zeq = 30+10j ()
vG(t) = VM cos(1000t) V
Il circuito è in condizioni di regime sinusoidale. N1, N2, N3 sono le potenze complesse assorbite dai bipoli
1, 2, 3 e NG è la potenza complessa erogata dal generatore vG. Zeq è l’impedenza equivalente del bipolo
racchiuso dalla linea tratteggiata. Determinare:
1. l’ampiezza VM della tensione del generatore;
2. le espressioni della tensione vR(t) e della corrente iL(t);
3. i valori della resistenza R e dell’induttanza L.
Elettrotecnica - A.A. 2011-12 - Prova n. 2 – 27 gennaio 2012
Domande
1.
1
Il carico trifase rappresentato in figura viene
alimentato con una terna diretta simmetrica
di tensioni concatenate avente valore efficace
Veff = 300 3 V. Determinare il valore efficace Ieff delle correnti di linea e il fattore di
potenza FP del carico. (2 punti)
Ieff
FP
C
C
C
L
L
R = 30
2.
Assumendo che tutti i traferri abbiano riluttanza uguale a R0 e che le riluttanze dei tratti
in materiale ferromagnetico siano trascurabili, determinare il coefficiente di mutua induzione dei due avvolgimenti. (2 punti)
R
L
R
L = 60
i1
R
1/C = 10
i2
N1
N2
M
L
3.
Determinare la potenza disponibile del bipolo
AB e il valore dell’impedenza ZC con cui si
ottiene il massimo trasferimento di potenza
attiva. (2 punti)
PD
ZC
iG
R
A
C
ZC
B
iG(t) = 2cos(t) A
R= 10 L = 10 1/(C) = 10
4.
Un trasformatore ideale con rapporto di trasformazione 4 con i terminali del secondario collegati ad
un resistore da 10 equivale a un resistore da
40
160
2.5
5.
6.
7.
Si consideri il comportamento al variare della pulsazione di un bipolo RLC serie alimentato da un
generatore di corrente sinusoidale. In condizioni di risonanza l’ampiezza della tensione del bipolo è
massima
nulla
minima
L’integrale lungo una linea chiusa del potenziale vettore magnetico A
è nullo
è uguale al flusso di induzione magnetica concatenato con la linea
è uguale alla corrente concatenata con la linea
Si considerino due bipoli passivi in condizione di regime sinusoidale collegati in serie. Se le potenze
attive assorbite dai due bipoli sono uguali
è maggiore l’ampiezza della tensione del bipolo avente il fattore di potenza minore
le ampiezze delle tensioni dei bipoli sono uguali
è maggiore l’ampiezza della tensione del bipolo avente il fattore di potenza maggiore
Elettrotecnica - A.A. 2011-12 - Prova n. 2 – 27 gennaio 2012
Cognome
Nome
E1
Parti svolte:
E2
Matricola
Firma
2
D
Esercizio 1
A
gV1
R7
R8
R5
E
B
IG8
C
1. indicare quali grandezze vengono scelte
come incognite del sistema risolvente
VG4
R1
R2
Supponendo noti i valori delle resistenze,
della tensione VG4, della corrente IG8 e del
parametro di trasferimento del generatore dipendente, illustrare il procedimento di risoluzione del circuito rappresentato in figura con
il metodo delle tensioni di nodo:
R3
2. scrivere il sistema risolvente
3. scrivere le espressioni in funzione delle
incognite indicate al punto 1
a. delle tensioni dei resistori
b. delle potenze erogate dai generatori
D
Esercizio 2
iG
vG
i1
1
i3
3
i2
iR
R
2
C
vC
N1 = 80240j (W, Var)
N2 = 80160j (W, Var)
N3 = 160+160j (W, Var)
NG = 480160j (W, Var)
Zeq = 6+2j ()
vG(t) = VM cos(1000t) V
Il circuito è in condizioni di regime sinusoidale. N1, N2, N3 sono le potenze complesse assorbite dai bipoli
1, 2, 3 e NG è la potenza complessa erogata dal generatore vG. Zeq è l’impedenza equivalente del bipolo
racchiuso dalla linea tratteggiata. Determinare:
1. l’ampiezza VM della tensione del generatore;
2. le espressioni della corrente iG(t) e della tensione vC(t);
3. i valori della resistenza R e della capacità C.
Elettrotecnica - A.A. 2011-12 - Prova n. 2 – 27 gennaio 2012
Domande
1.
2
Il carico trifase rappresentato in figura viene
alimentato con una terna diretta simmetrica
di tensioni concatenate avente valore efficace
Veff = 300 3 V. Determinare il valore efficace Ieff delle correnti di linea e il fattore di
potenza FP del carico. (2 punti)
Ieff
FP
R
R
R
L
L
R = 50
2.
Assumendo che tutti i traferri abbiano riluttanza uguale a R0 e che le riluttanze dei tratti
in materiale ferromagnetico siano trascurabili, determinare il coefficiente di mutua induzione dei due avvolgimenti. (2 punti)
L
C
L = 75
C
C
1/C = 45
i1
i2
N1
N2
M
R
3.
Determinare la potenza disponibile del bipolo
AB e il valore dell’impedenza ZC con cui si
ottiene il massimo trasferimento di potenza
attiva. (2 punti)
PD
ZC
iG
C
A
L
ZC
B
iG(t) = 6cos(t) A
R= 2 L = 2 1/(C) = 2
4.
Un trasformatore ideale con rapporto di trasformazione 3 con i terminali del secondario collegati ad
un resistore da 6 equivale a un resistore da
54
18
3
5.
6.
7.
Si consideri il comportamento al variare della pulsazione di un bipolo RLC serie alimentato da un
generatore di tensione sinusoidale. In condizioni di risonanza l’ampiezza della corrente nel bipolo è
nulla
minima
massima
Il potenziale vettore magnetico A è definito a meno
di una costante
del gradiente di una funzione scalare
di un vettore costante
Si considerino due bipoli passivi in condizione di regime sinusoidale collegati in parallelo. Se le potenze attive assorbite dai due bipoli sono uguali
è maggiore l’ampiezza della corrente del bipolo avente il fattore di potenza minore
è maggiore l’ampiezza della corrente del bipolo avente il fattore di potenza maggiore
le ampiezze delle correnti dei bipoli sono uguali
Elettrotecnica - A.A. 2011-12 - Prova n. 2 – 27 gennaio 2012
Cognome
Nome
E1
Parti svolte:
E2
Matricola
Firma
3
D
Esercizio 1
A
R1
mV5
R4
IG7
C
B
D
R2
R3
R5
VG6
Supponendo noti i valori delle resistenze,
della tensione VG6, della corrente IG7 e del
parametro di trasferimento del generatore dipendente, illustrare il procedimento di risoluzione del circuito rappresentato in figura con
il metodo delle correnti di maglia:
1. indicare quali grandezze vengono scelte
come incognite del sistema risolvente
R8
2. scrivere il sistema risolvente
3. scrivere le espressioni in funzione delle
incognite indicate al punto 1
a. delle correnti dei resistori
b. delle potenze erogate dai generatori
E
Esercizio 2
C
vG
vC
i2
2
i3
i1
1
3
iR
R
N1 = 100300j (W, Var)
N2 = 100+300j (W, Var)
N3 = 200+200j (W, Var)
NG = 600j (W, Var)
Zeq = 3010j ()
vG(t) = VM cos(1000t) V
Il circuito è in condizioni di regime sinusoidale. N1, N2, N3 sono le potenze complesse assorbite dai bipoli
1, 2, 3 e NG è la potenza complessa erogata dal generatore vG. Zeq è l’impedenza equivalente del bipolo
racchiuso dalla linea tratteggiata. Determinare:
1. l’ampiezza VM della tensione del generatore;
2. le espressioni della tensione vC(t) e della corrente iR(t);
3. i valori della resistenza R e della capacità C.
Elettrotecnica - A.A. 2011-12 - Prova n. 2 – 27 gennaio 2012
Domande
1.
3
Il carico trifase rappresentato in figura viene
alimentato con una terna diretta simmetrica
di tensioni concatenate avente valore efficace
Veff = 300 3 V. Determinare il valore efficace Ieff delle correnti di linea e il fattore di
potenza FP del carico. (2 punti)
Ieff
FP
L
L
L
R
R
R = 90
2.
Assumendo che tutti i traferri abbiano riluttanza uguale a R0 e che le riluttanze dei tratti
in materiale ferromagnetico siano trascurabili, determinare il coefficiente di mutua induzione dei due avvolgimenti. (2 punti)
R
C
L = 30
C
C
1/C = 45
i1
i2
N1
N2
M
C
3.
Determinare la potenza disponibile del bipolo
AB e il valore dell’impedenza ZC con cui si
ottiene il massimo trasferimento di potenza
attiva. (2 punti)
PD
ZC
iG
R
A
L
ZC
B
iG(t) = 8cos(t) A
R= 5 L = 5 1/(C) = 5
4.
Un trasformatore ideale con rapporto di trasformazione 5 con i terminali del secondario collegati ad
un resistore da 20 equivale a un resistore da
4
100
500
5.
6.
7.
Si consideri il comportamento al variare della pulsazione di un bipolo RLC parallelo alimentato da un
generatore di corrente sinusoidale. In condizioni di risonanza l’ampiezza della tensione del bipolo è
minima
nulla
massima
L’integrale lungo una linea chiusa del potenziale vettore magnetico A
è nullo
è uguale al flusso di induzione magnetica concatenato con la linea
è uguale alla corrente concatenata con la linea
Si considerino due bipoli passivi in condizione di regime sinusoidale collegati in parallelo. Se le potenze attive assorbite dai due bipoli sono uguali
è maggiore l’ampiezza della corrente del bipolo avente il fattore di potenza minore
è maggiore l’ampiezza della corrente del bipolo avente il fattore di potenza maggiore
le ampiezze delle correnti dei bipoli sono uguali
Elettrotecnica - A.A. 2011-12 - Prova n. 2 – 27 gennaio 2012
Cognome
Nome
E1
Parti svolte:
E2
Matricola
Firma
4
D
Esercizio 1
A
R1
R4
R7
R6
E
B
aI6
VG3
R2 IG5
C
Supponendo noti i valori delle resistenze,
della tensione VG3, della corrente IG5 e del
parametro di trasferimento del generatore dipendente, illustrare il procedimento di risoluzione del circuito rappresentato in figura con
il metodo delle tensioni di nodo:
1. indicare quali grandezze vengono scelte
come incognite del sistema risolvente
R8
2. scrivere il sistema risolvente
3. scrivere le espressioni in funzione delle
incognite indicate al punto 1
a. delle tensioni dei resistori
b. delle potenze erogate dai generatori
D
Esercizio 2
iG
i1
iL
vG
1
i3 3
i2
L
2
R
vR
N1 = 50100j (W, Var)
N2 = 100+200j (W, Var)
N3 = 5050j (W, Var)
NG = 250500j (W, Var)
Zeq = 4+8j ()
vG(t) = VM cos(1000t) V
Il circuito è in condizioni di regime sinusoidale. N1, N2, N3 sono le potenze complesse assorbite dai bipoli
1, 2, 3 e NG è la potenza complessa erogata dal generatore vG. Zeq è l’impedenza equivalente del bipolo
racchiuso dalla linea tratteggiata. Determinare:
1. l’ampiezza VM della tensione del generatore;
2. le espressioni della corrente iG(t) e della tensione vR(t);
3. i valori della resistenza R e dell’induttanza L.
Elettrotecnica - A.A. 2011-12 - Prova n. 2 – 27 gennaio 2012
Domande
1.
4
Il carico trifase rappresentato in figura viene
alimentato con una terna diretta simmetrica
di tensioni concatenate avente valore efficace
Veff = 300 3 V. Determinare il valore efficace Ieff delle correnti di linea e il fattore di
potenza FP del carico. (2 punti)
Ieff
FP
R
R
R
C
C
R = 30
2.
Assumendo che tutti i traferri abbiano riluttanza uguale a R0 e che le riluttanze dei tratti
in materiale ferromagnetico siano trascurabili, determinare il coefficiente di mutua induzione dei due avvolgimenti. (2 punti)
C
L
L = 45
L
L
1/C = 60
i1
i2
N1
N2
M
R
3.
Determinare la potenza disponibile del bipolo
AB e il valore dell’impedenza ZC con cui si
ottiene il massimo trasferimento di potenza
attiva. (2 punti)
PD
ZC
iG
L
A
C
ZC
B
iG(t) = 4cos(t) A
R= 3 L = 3 1/(C) = 3
4.
Un trasformatore ideale con rapporto di trasformazione 10 con i terminali del secondario collegati ad
un resistore da 30 equivale a un resistore da
3000
300
3
5.
6.
7.
Si consideri il comportamento al variare della pulsazione di un bipolo RLC parallelo alimentato da un
generatore di tensione sinusoidale. In condizioni di risonanza l’ampiezza della corrente nel bipolo è
minima
massima
nulla
Il potenziale vettore magnetico A è definito a meno
di una costante
del gradiente di una funzione scalare
di un vettore costante
Si considerino due bipoli passivi in condizione di regime sinusoidale collegati in serie. Se le potenze
attive assorbite dai due bipoli sono uguali
è maggiore l’ampiezza della tensione del bipolo avente il fattore di potenza minore
le ampiezze delle tensioni dei bipoli sono uguali
è maggiore l’ampiezza della tensione del bipolo avente il fattore di potenza maggiore