Moduli

I ANNO
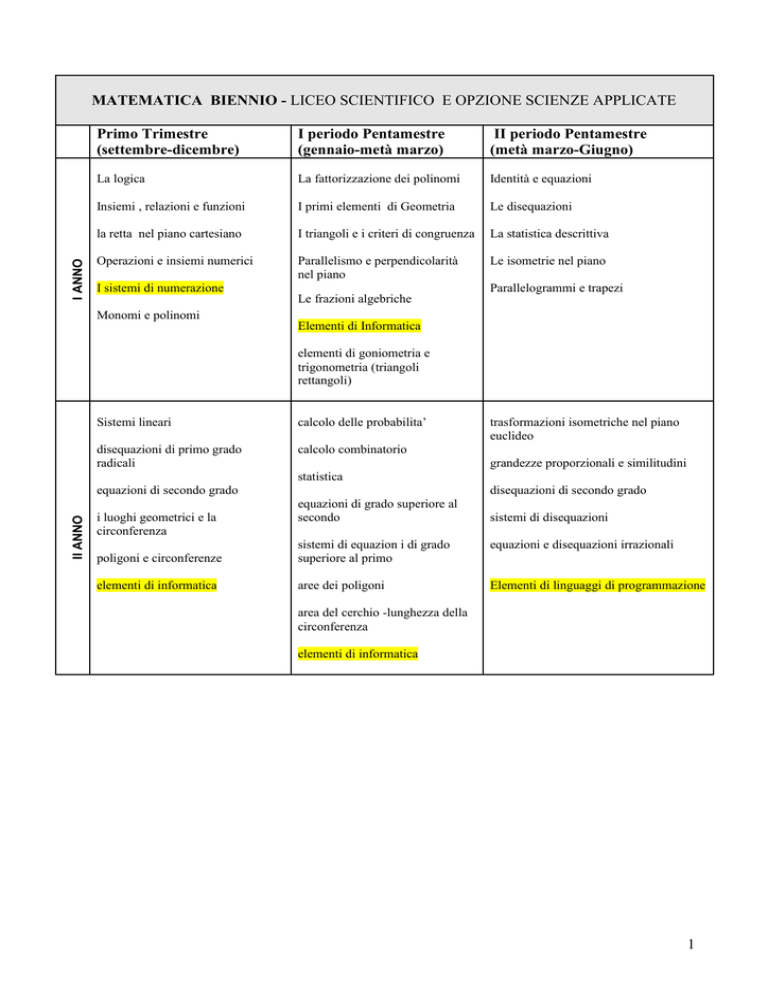
MATEMATICA BIENNIO - LICEO SCIENTIFICO E OPZIONE SCIENZE APPLICATE
Primo Trimestre
(settembre-dicembre)
I periodo Pentamestre
(gennaio-metà marzo)
II periodo Pentamestre
(metà marzo-Giugno)
La logica
La fattorizzazione dei polinomi
Identità e equazioni
Insiemi , relazioni e funzioni
I primi elementi di Geometria
Le disequazioni
la retta nel piano cartesiano
I triangoli e i criteri di congruenza
La statistica descrittiva
Operazioni e insiemi numerici
Parallelismo e perpendicolarità
nel piano
Le isometrie nel piano
I sistemi di numerazione
Monomi e polinomi
Le frazioni algebriche
Parallelogrammi e trapezi
Elementi di Informatica
elementi di goniometria e
trigonometria (triangoli
rettangoli)
Sistemi lineari
calcolo delle probabilita’
disequazioni di primo grado
radicali
calcolo combinatorio
trasformazioni isometriche nel piano
euclideo
grandezze proporzionali e similitudini
statistica
II ANNO
equazioni di secondo grado
i luoghi geometrici e la
circonferenza
disequazioni di secondo grado
equazioni di grado superiore al
secondo
sistemi di disequazioni
sistemi di equazion i di grado
superiore al primo
equazioni e disequazioni irrazionali
poligoni e circonferenze
elementi di informatica
aree dei poligoni
Elementi di linguaggi di programmazione
area del cerchio -lunghezza della
circonferenza
elementi di informatica
1
I ANNO
MATEMATICA BIENNIO - LICEO LINGUISTICO
Primo Trimestre
(settembre-dicembre)
I periodo Pentamestre
(gennaio-metà marzo)
II periodo Pentamestre
(metà marzo-Giugno)
Insiemi
Monomi e polinomi
Le equazioni
Gli insiemi numerici
La fattorizzazione dei polinomi
La statistica descrittiva
Operazioni con gli insiemi numerici
I triangoli e i criteri di congruenza
Le isometrie nel piano
I sistemi di numerazione
Parallelismo e perpendicolarità
nel piano
Parallelogrammi e trapezi
I primi elementi di Geometria
Le frazioni algebriche
la retta e i sistemi lineari
calcolo delle probabilita’
disequazioni di primo grado
radicali
calcolo combinatorio
Elementi di Informatica
trasformazioni isometriche nel piano
euclideo
grandezze proporzionali e similitudini
statistica
II ANNO
equazioni di secondo grado
i luoghi geometrici e la
circonferenza
disequazioni di secondo grado
equazioni di grado superiore al
secondo
poligoni e circonferenze
sistemi di equazion i di grado
superiore al primo
elementi di informatica
aree dei poligoni
sistemi di disequazioni
equazioni e disequazioni irrazionali
primi elementi di trigonometria
Elementi di linguaggi di programmazione
area del cerchio -lunghezza della
circonferenza
elementi di informatica
2
RIFORMAIII
MATEMATICA TRIENNIO - LICEO SCIENTIFICO
Primo Trimestre
(settembre-dicembre)
I periodo Pentamestre
(gennaio-metà marzo)
II periodo Pentamestre
(metà marzo-Giugno)
Disequazioni ( fratte, Irrazionali,
con valore assoluto)
Parabola (definizioni – retta
tangente –fasci di parabole)
Iperbole (definizioni – retta tangente –
fasci, funzione omografica)
Retta (equazioni – parallelismo –
perpendicolarità – coefficiente
angolare – fasci di rette)
Ellisse (definizioni – retta
tangente)
Circonferenza e cerchio (definizioni
– retta tangente – fasci di
circonferenze)
Isometrie (traslazione –
rotazione –simmetriatrasformazioni geometriche)
Formule di addizione, duplicazione
e bisezione (come
approfondimento del biennio)
RIFORMAIV
Approfondimenti di Trigonometria:
Il teorema della corda, il teorema
dei seni e il teorema del coseno per
la risoluzione dei triangoli.
Risoluzione approssimata di equazioni
Numeri complessi e applicazioni
Sistemi lineari (Regola di Cramer teorema di Rouchè-Capelli- sistemi
con parametro)
V NON PNI
Funzioni: (esistenza –intersezione
assi –positività)
Statistica Descrittiva: richiami ed
approfondimenti
Elementi di statistica descrittiva bivariata
Successioni: Principio di induzione,
Progressioni aritmetiche e geometriche
Affinità
Logaritmi (definizioni - equazioni
– disequazioni)
Funzione esponenziale
(definizioni - equazioni –
disequazioni)
Approfondimento sulle equazioni
esponenziali e logaritmiche
Problemi Geometrici di I e II
grado dipendenti
eventualmente da un parametro
Derivabilità (definizioni –
massimi e minimi – flessi)
Limiti (definizioni – calcolo dei
limiti limiti di successioni - limiti di
funzione - calcolo)
Studio e rappresentazione grafica
di una funzione
Continuità (definizioni –
discontinuità)
Risoluzione approssimata di
equazioni.
Risoluzione approssimata di
equazioni.
Geometria solida (Incidenza,
parallelismo e ortogonalità nello spazio,
teorema delle tre perpendicolari)
Geometria solida (aree e volumi di solidi,
principio di Cavalieri)
Statistica Descrittiva: richiami ed
approfondimenti
Calcolo Combinatorio
Probabilità(eventi, teoremi di calcolo
delle probabilità, probabilità totale e
composta, Teorema di Bayes)
Integrali definiti e indefiniti
Calcolo di aree e volumi utilizzando il
calcolo integrale
Temi di esame
Probabilità (Legge dei grandi numeri
(Bernoulli) - Formula di Bayes)
Integrale definito: volumi
V PNI
Derivabilità (definizioni – massimi
e minimi – flessi)
Studio e rappresentazione grafica
di una funzione
Derivabilità (definizioni – massimi
e minimi – flessi)
Calcolo Combinatorio
(disposizioni – permutazioni –
combinazioni)
Statistica (Variabili aleatorie discrete Interpolazione, regressione e
correlazione)
Probabilità ( nei vari contesti, nel
discreto e nel continuo)
Distribuzioni ( continue - Distribuzione
normale ed errori di misura nelle scienze
sperimentali)
Informatica: file testo
Temi di esame
Studio e rappresentazione grafica
di una funzione
Informatica: file testo
3
RIFORMAIII
MATEMATICA TRIENNIO - LICEO LINGUISTICO
Primo Trimestre
(settembre-dicembre)
I periodo Pentamestre
(gennaio-metà marzo)
Sistemi lineari con il metodo di
Cramer e determinante di matrici
Parabola (definizioni – retta tangente
–fasci di parabole)
Equazioni e Disequazioni ( richiami
su quelle di 1° grado e di 2° grado;
di 2° grado con metodo grafico e
metodi rapidi di risoluzione per
disequazioni pure e spurie; fratte,
Irrazionali, con valore assoluto)
Retta (equazioni – parallelismo –
perpedicolarità – coefficiente
angolare – fasci di rette – distanza tra
due punti – retta passante per 2 punti
– retta passante per un punto e
parallela o perpendicolare ad una
retta data – distanza di un punto da
una retta).
Punto medio di un segmento.
Baricentro di un triangolo.
Asse di un segmento
Fattorizzazione di semplici
polinomi . Disequazioni di grado
superiore al secondo già scomposte
in fattori.
Funzioni e loro caratteristiche;
funzioni lineari, quadratiche,
polinomiali e loro grafici; zeri di
una funzione.
Sistemi di disequazioni.
Goniometria (principali formule
goniometriche – teorema della
corda -teorema dei seni – teorema
di Carnot - equazioni e disequazioni
Trigonometria (relazioni tra angoli e
lati- risoluzione dei triangoli
qualsiasi)
RIFORMAIV
V
Funzione esponenziale (definizioni equazioni – disequazioni)
Limiti (definizioni – calcolo dei
limiti limiti di successioni - limiti di
funzione - calcolo)
Continuità (definizioni –
discontinuità)
Ellisse (definizioni – retta tangente –
fasci)
Iperbole (definizioni – retta tangente –
fasci, funzione omografica)
Progressioni (aritmetiche, geometriche)
Poligoni, retta, parabola, circonferenza
con Cabri Géomètre .
Risolvere problemi utilizzando equazioni
di secondo grado
Geometria solida (Incidenza,
parallelismo e ortogonalità nello spazio)
Statistica Descrittiva: richiami ed
approfondimenti
Calcolo Combinatorio
Approfondimento sulle equazioni
esponenziali e logaritmiche
Funzioni: (esistenza –intersezione
assi –positività)
Circonferenza e cerchio (definizioni –
retta tangente – fasci di circonferenze)
Foglio elettronico con Excel.
Le funzioni con Excel
Logaritmi (definizioni - equazioni –
disequazioni)
Trigonometria (relazioni tra angoli
e lati- risoluzione dei triangoli
rettangoli)
II periodo Pentamestre
(metà marzo-Giugno)
Derivabilità (definizioni – massimi e
minimi – flessi)
Studio e rappresentazione grafica di
una funzione
Probabilità(eventi, teoremi di calcolo
delle probabilità, probabilità totale e
composta, Teorema di Bayes)
Integrali definiti e indefiniti
Calcolo di aree e volumi utilizzando il
calcolo integrale
Temi di esame
Risoluzione approssimata di
equazioni.
4
I RIFORMA
FISICA - LICEO SCIENTIFICO E OPZIONE SCIENZE APPLICATE
Primo Trimestre
(settembre-dicembre)
I periodo Pentamestre
(gennaio-metà marzo)
Il Metodo scientifico.
Le forze e l’equilibrio dei corpi
II periodo Pentamestre
(metà marzo-Giugno)
Le forze e il movimento
Le grandezze fisiche. Gli errori di
misura
Le Leve
Moto uniforme.
Relazioni tra grandezze
Equilibrio nei fluidi
Moto uniformemente accelerato
II RIFORMA
Vettori e scalari
Temperatura e calore
Moti nel Piano
La luce
I principi della dinamica.
Sistemi di riferimento Inerziali e non
inerziali
Le leggi del moto
RIFORMAIII
L’energia meccanica
Moto del proiettile, moto parabolico e
moto nel piano inclinato
Moti Circolari e Oscillatori
Energia Meccanica
Gravitazione universale
Calore e temperatura
(Termometro- dilatazione – Calore e
lavoro – Capacità termica- calore
specifico)
Stati della materia e cambiamenti di
stato
(fusione-solidificazionevaporizzazione – condensazione –
sublimazione –temperatura critica)
Primo principio della
Termodinamica
(Energi interna- principio zerotrasformazioni – lavoro- applicazioni)
Secondo principio della
termodinamica
(macchine termiche- i vari enunciati
– ciclo di Carnot- il motore
dell’automobile – il frigorifero)
Entropia
Quantità di moto e urti
Momento di una forza
IV RIFORMA
Eventuale completamento della
termodinamica .
Onde
(onde elastiche- fronti d’ondaperiodiche – armoniche – interferenza)
Il suono
(caratteristiche -eco- onde stazionarie
effetto Doppler)
V
La riflessione e gli specchi
(leggi della riflessione – costruzione
delle immagini- esempi - applicazioni)
La carica e Legge di Coulomb
(La carica elettrica – elettrizzazione –
strofinio- conduttori e isolanti – la
legge)
Il campo elettrico
(definizione – flusso - teorema di
gauss – applicazioni – il potenziale)
La corrente elettrica
(Resistenza - Leggi di Ohm – effetto
Joule – condensatori)
La rifrazione e le lenti
(leggi della riflrazione –
costruzione delle immagini- esempi
- applicazioni)
Ottica fisica
(onde- corpuscoli- interferenzadiffrazione- colori)
La carica e Legge di Coulomb
(La carica elettrica – elettrizzazione
– strofinio- conduttori e isolanti – la
legge)
Il campo elettrico
(definizione – flusso - teorema di
gauss – applicazioni – il potenziale)
La corrente elettrica
(Resistenza - Leggi di Ohm – effetto
Joule – condensatori)
circuiti elettrici
(Resistenze in serie e parallelo – leggi
di Kirchhoff- forza elettromotrice)
Il campo magnetico
(fenomeni magnetici)
circuiti elettrici
(Resistenze in serie e parallelo –
leggi di Kirchhoff- forza
elettromotrice)
Il campo magnetico
(fenomeni magnetici – spira
solenoide motorino elettrico- forza
di Lorentz – legge di Lenz –
induzione –autoinduzione)
Onde elettromagnetiche
(polarizzazione – spettro- onde radio
– microonde – radiazioni – radio –
televisori – cellulari)
5
III
FISICA - LICEO LINGUISTICO
Primo Trimestre
(settembre-dicembre)
I periodo Pentamestre
(gennaio-metà marzo)
II periodo Pentamestre
(metà marzo-Giugno)
Le forze e le grandezze vettoriali
Principi della dinamica
Il lavoro e l’energia
Equilibrio dei solidi
Composizione dei moti
La quantità di moto e gli urti
Equilibrio nei fluidi
Moto rettilineo
Gravitazione universale
IV
Calore e temperatura
(Termometro- dilatazione – Calore e
lavoro – Capacità termica- calore
specifico)
Stati della materia e cambiamenti di
stato
(fusione-solidificazionevaporizzazione – condensazione –
sublimazione –temperatura critica)
Primo principio della Termodinamica
(Energi interna- principio zerotrasformazioni – lavoro- applicazioni)
Secondo principio della termodinamica
(macchine termiche- i vari enunciati –
ciclo di Carnot- il motore
dell’automobile – il frigorifero)
Entropia
Onde
(onde elastiche- fronti d’ondaperiodiche – armoniche – interferenza)
Il suono
(caratteristiche -eco- onde stazionarie
effetto Doppler)
La riflessione e gli specchi
(leggi della riflessione –
costruzione delle immaginiesempi - applicazioni)
La rifrazione e le lenti
(leggi della riflrazione –
costruzione delle immaginiesempi - applicazioni)
Ottica fisica
(onde- corpuscoli- interferenzadiffrazione- colori)
6
I ANNO
INFORMATICA LICEO SCIENTIFICO - OPZIONE SCIENZE APPLICATE
Primo Trimestre
(settembre-dicembre)
I periodo Pentamestre
(gennaio-metà marzo)
Le componenti fondamentali di un
sistema di elaborazione
Elaborazione digitale
documento: Word
La
rappresentazione
informazioni
La creazione di presentazioni
multimediali con Power Point
delle
di
II periodo Pentamestre
(metà marzo-Giugno)
un
Il foglio di calcolo Excel
Ripasso rappresentazione dei dati
interi, reali ed alfanumerici
Le strutture di controllo
Dall’algoritmo al programma
Utilizzo
di
un
linguaggio
di
programmazione per la codifica degli
algoritmi
Funzioni avanzate di Excel
Dal problema all’algoritmo
Le reti di computer e Internet
(si completa il lavoro iniziato nel
precedente a. s.)
III ANNO
II ANNO
Il sistema operativo: funzionalità di
base e le caratteristiche dei sistemi
operativi più comuni
INFORMATICA III anno DA DEFINIRE
(Dalle indicazioni nazionali)
Nel secondo biennio si procede ad un allargamento della padronanza di alcuni strumenti e un
approfondimento dei loro fondamenti concettuali. La scelta dei temi dipende dal contesto e dai rapporti
che si stabiliscono fra l’informatica e le altre discipline. Sarà possibile disegnare un percorso all'interno
delle seguenti tematiche: strumenti avanzati di produzione dei documenti elettronici, linguaggi di
markup (XML etc), formati non testuali (bitmap, vettoriale, formati di compressione), font tipografici,
progettazione web (DE); introduzione al modello relazionale dei dati, ai linguaggi di interrogazione e
manipolazione dei dati (BS); implementazione di un linguaggio di programmazione, metodologie di
programmazione, sintassi di un linguaggio orientato agli oggetti (AL).
7