Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
C.S. Chimica – Università degli Studi di Torino
Corso di Fisica C
A.A. 2002-2003
Relazioni del gruppo
___________________________________________
___________________________________________
___________________________________________
___________________________________________
___________________________________________
___________________________________________
1
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
2
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
Esperienza 1 - Oscilloscopio e generatore di funzioni
Studenti presenti (firme): __________________________________________________________________
1 Visualizzazione di una traccia sull'oscilloscopio
Che cosa appare sull’oscilloscopio quando
è stato acceso, sono stati selezionati i
comandi seguenti sui 4 selettori relativi al
controllo del TRIGGER: AUTO, DC
COUPLING, SOURCE, INT X-Y, CH.1
ed è stata selezionata sul selettore dei
tempi una velocità di spazzata di 1 ms/div
(1 divisione = 1 cm in orizzontale sullo
schermo), calibrata?
Che cosa significa velocità di spazzata di 1
ms/div?
Quando viene impostata una velocità di
spazzata superiore ad 1 ms/div, il puntino
luminoso si muove più o meno
velocemente? Perché?
Selezionare una velocità di spazzata di 1
s/div. Quanto tempo impiega il puntino
luminoso a percorrere l’intero schermo in
orizzontale?
Che relazione c’è nel caso precedente tra
velocità di spazzata e tempo impiegato a
percorrere l’intero schermo?
2 Misure di ampiezze e periodi
Una volta che venga visualizzata la forma
d’onda più o meno stabile sullo schermo,
che cosa accade regolando il selettore
relativo all’ampiezza del segnale?
E che cosa accade regolando invece il
selettore relativo alla velocità di
spazzata?
3
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
Pers
Provare a valutare l’ampiezza
picco-picco (in verticale) ed il
periodo (in orizzontale) del
segnale contando il numero di
divisioni grandi e piccole e
moltiplicandole per il fattore di
conversione sul selettore. Ripetere i
calcoli per ogni persona
componente il gruppo e cambiando
eventualmente la mano (destrasinistra). Convertite quindi la
misura di periodo in frequenza. Per
ogni misura valutate anche l’errore.
Div.
Amp.
Div.
Ampiezza periodo
Periodo
Frequenza
1
___±0.2 ____±____ ___±0.2 ____±____ ____±____
2
___±0.2 ____±____ ___±0.2 ____±____ ____±____
3
___±0.2 ____±____ ___±0.2 ____±____ ____±____
4
___±0.2 ____±____ ___±0.2 ____±____ ____±____
5
___±0.2 ____±____ ___±0.2 ____±____ ____±____
6
___±0.2 ____±____ ___±0.2 ____±____ ____±____
7
___±0.2 ____±____ ___±0.2 ____±____ ____±____
8
___±0.2 ____±____ ___±0.2 ____±____ ____±____
9
___±0.2 ____±____ ___±0.2 ____±____ ____±____
10 ___±0.2 ____±____ ___±0.2 ____±____ ____±____
C’è analogia tra il valore di frequenza
atteso (50 Hz) e quello letto?
Provare a diminuire o aumentare la scala
delle ampiezze e quella dei tempi, e
ripetere una misura. Tenendo conto che
l’errore della vostra rilevazione è di una
divisione piccola (=0.2 divisioni grandi,
poiché ce ne sono 5), ne concludete che è
meglio visualizzare un singolo tratto
dell’onda a tutto schermo oppure no?
Perché?
Scala normale
Ampiezza: _____±0.2 div à _______±_______
Periodo: _____±0.2 div à _______±_______
Scala ridotta
Ampiezza: _____±0.2 div à _______±_______
Periodo: _____±0.2 div à _______±_______
Scala ingrandita
Ampiezza: _____±0.2 div à _______±_______
Periodo: _____±0.2 div à _______±_______
3 Visualizzazione di un segnale dal generatore
Frequenza nominale: 1 KHz
Dopo avere impostato un'onda sinusoidale
proveniente dal generatore di funzioni in
Ampiezza nominale: _________
modo di funzionamento NORMAL,
regolato con frequenza 1 kHz, ampiezza di
qualche V (<10 V) ed offset 0 V, che cosa Periodo misurato: _____±0.2 div à _______±_______
osservate sull’oscilloscopio? Determinare
il numero di divisioni piccole e grandi
Frequenza misurata: ___________±__________
relative a periodo ed ampiezza dell’onda,
e confrontarle con i valori di input.
4
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
e confrontarle con i valori di input.
Che cosa accade selezionando la
posizione di calibrazione variabile per
l’ampiezza dell’onda? È possibile
misurare l’ampiezza dell’onda in questo
caso? Provare a farlo. Che cosa notate?
Ampiezza misurata: _____±0.2 div à ______±_____
Ampiezza nominale: _______________
Ampiezza con posizione di calibrazione fissa:
_________±0.2 div à __________±__________
Ampiezza con posizione di calibrazione variabile:
_________±0.2 div à __________±__________
Frequenza nominale: _______________
Periodo con posizione di calibrazione fissa:
Che cosa accade selezionando la
posizione di calibrazione variabile per il
periodo dell’onda? È possibile misurare il
periodo dell’onda in questo caso? Provare
a farlo, e poi convertire in frequenza. Che
cosa notate?
_________±0.2 div à __________±__________
Frequenza: __________±__________
Periodo con posizione di calibrazione variabile:
_________±0.2 div à __________±__________
Frequenza: __________±__________
Posizionare il selettore del trigger in
posizione AUTO, quindi variare il livello
del trigger (LEVEL). È sempre visibile
l’onda? Se no, quando cessa di essere
visibile? Determinare (contando le
divisioni) il valore numerico per il quale
parte e cessa la porzione visibile
dell’onda.
Ripetere le osservazioni precedenti
posizionando il selettore del trigger in
posizione NORM. Variando il livello del
trigger (LEVEL), è sempre visibile
l’onda? Se no, quando cessa di essere
visibile? Determinare (contando le
divisioni) il valore numerico per il quale
parte e cessa la porzione visibile
dell’onda.
Impostare il selettore relativo al canale
sulla posizione DC. Quindi impostare sul
generatore di funzioni un offset (piccolo)
diverso da zero. Quale tipo di segnale si
vede sullo schermo? Che cosa rappresenta
matematicamente l’offset? Impostare un
offset piccolo in modo che l’onda
“rimanga sullo schermo” e valutare la
posizione del massimo e del minimo
dell’onda e la sua ampiezza con e senza
offset. Discutere il risultato.
Variare la posizione del selettore del
canale dalla posizione DC alla posizione
AC e prendere le misure dei minimi e dei
Valore minimo:
_________±0.2 div à __________±__________
Valore massimo:
_________±0.2 div à __________±__________
Valore minimo:
_________±0.2 div à __________±__________
Valore massimo:
_________±0.2 div à __________±__________
Offset = 0
Min.: ________±0.2 div à __________±__________
Max.: ________±0.2 div à __________±__________
Offset = _______
Min.: ________±0.2 div à __________±__________
Max.: ________±0.2 div à __________±__________
Posizione DC
Min.: ________±0.2 div à __________±__________
5
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
massimi dell’onda.
Max.: ________±0.2 div à __________±__________
Posizione AC
Min.: ________±0.2 div à __________±__________
Max.: ________±0.2 div à __________±__________
Che tipo di segnale si ottiene adesso?
Quale è la funzione del selettore in
posizione AC rispetto alla posizione DC?
4 Misure di ampiezza, periodo e tempo di salita di segnali
Misurare sull’oscilloscopio sul canale 1
Frequenza nominale: 1 KHz
ampiezza picco-picco e periodo di un
segnale
sinusoidale
impostato
sul Periodo misurato: _____±0.2 div à _______±_______
generatore un segnale sinusoidale con
frequenza 1 kHz, ampiezza qualche volt e
Frequenza misurata: ___________±__________
offset 0 V. Determinarne ampiezza e
frequenza e confrontare con i valori Ampiezza misurata: _____±0.2 div à ______±_____
nominali.
Frequenza nominale: 1 KHz
Misurare sull’oscilloscopio sul canale 2 Periodo misurato: _____±0.2 div à _______±_______
ampiezza picco-picco e periodo del
segnale di sincronismo del generatore.
Frequenza misurata: ___________±__________
Ampiezza misurata: _____±0.2 div à ______±_____
Descrivere la forma del segnale di
sincronismo del generatore.
Ampiezza nominale: _____±0.2 div à ______±_____
Ampiezza (radd.):
_____±0.2 div à ______±_____
Che cosa succede sul segnale di Ampiezza (dimez.): _____±0.2 div à ______±_____
sincronismo variando l’ampiezza del
Osservazioni:
segnale sinusoidale? Effettuare altre due
misure (ad es., raddoppiarlo e dimezzarlo).
6
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
Che cosa succede sul segnale di
sincronismo variando il periodo del
segnale sinusoidale? Anche in questo
caso effettuare altre due misure (ad es.,
raddoppiare il periodo e dimezzarlo) e
commentarle.
Misurare sull’oscilloscopio il tempo di
salita dal 10% al 90% del valore
massimo di un segnale a onda quadra di
frequenza 100 kHz usando le apposite
linee orizzontali tratteggiate sullo schermo
dell'oscilloscopio. A questo proposito,
viene utile calibrare l’ampiezza del
segnale in modo che base e top dell’onda
coincidano con le linee tratteggiate “0” e
“100”.
Periodo nominale: _____±0.2 div à ______±_____
Frequenza nominale: ___________±__________
Periodo (radd.): _____±0.2 div à ______±_____
Frequenza (radd.): ___________±__________
Periodo (dimez.): _____±0.2 div à ______±_____
Frequenza (dimez.): ___________±__________
Osservazioni:
Tempo di salita: ___________±0.2 div
⇓
_______________±______________
Frequenza
nominale
Fare una misura di periodo a frequenza
nominale di 10 Hz, 100 Hz, 1 kHz, 10
kHz, 100 kHz, 1 MHz; ricavare la
frequenza ed il suo errore e verificare che
corrisponda al valore selezionato.
10 Hz
100 Hz
1 KHz
10 KHz
100 KHz
1 MHz
Periodo
misurato
(div)
______±0.2
______±0.2
______±0.2
______±0.2
______±0.2
______±0.2
Periodo
misurato
Frequenza
misurata
_____±____
_____±____
_____±____
_____±____
_____±____
_____±____
_____±____
_____±____
_____±____
_____±____
_____±____
_____±____
7
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
Esperienza 2 – Circuiti in corrente continua
Studenti presenti (firme): __________________________________________________________________
1 Misure con resistenze in serie
Scegliere due resistenze in modo da
ottenere un valore di resistenza
equivalente (in serie) tra 100 Ω e 1 KΩ ;
misurarne i valori esatti (con i rispettivi
errori: ricordare che l’errore associato ad
una misura è il minimo tra lo 0.3% e
comunque non meno di 1 unità sulla cifra
meno significativa) e valutare la resistenza
equivalente attesa (con il suo errore).
Valutare quale deve essere la tensione
massima applicabile alle due resistenze
quando esse siano connesse in serie,
ipotizzando Pk<0.25 W. Valutare anche
l’errore relativo a tale misura. Non
applicare tensioni maggiori di detto
valore.
R1= __________±_____ Ω
R2= __________±_____ Ω
Req= __________±_____ Ω
Vmax= __________±_____ V
V1= __________±_____V
Determinare i valori attesi delle cadute di
tensione sulle resistenze, e la corrente
attesa nel circuito.
V2= __________±_____V
i= __________±_____A
Misurare tutte le d.d.p. nel circuito
inserendo opportunamente due voltmetri
contemporaneamente. Valutare i singoli
errori delle misure.
V1= __________±_____V
V2= __________±_____V
Confrontare i valori di d.d.p. misurati con
i valori attesi. Che cosa notate?
2 Misure con resistenze in parallelo
Scegliere due resistenze in modo da
ottenere un valore di resistenza
equivalente (in parallelo) tra 100 Ω e 1
KΩ ; misurarne i valori esatti e valutare la
resistenza equivalente attesa.
R1= __________±_____ Ω
R2= __________±_____ Ω
Req= __________±_____ Ω
8
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
Valutare quale deve essere la tensione
massima applicabile alle resistenze
quando esse siano connesse in serie,
ipotizzando Pk<0.25 W. Valutare anche
l’errore relativo a tale misura. Non
applicare tensioni maggiori di detto
valore.
Vmax= __________±_____ V
i1= __________±_____ A
Determinare i valori attesi delle correnti
nelle resistenze, e calcolare la corrente
totale.
i2= __________±_____ A
i= __________±_____ A
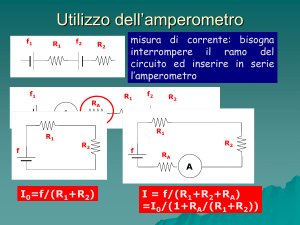
Misurare tutte le correnti (valutandone i
rispettivi errori) nel circuito inserendo
opportunamente due amperometri in
contemporanea. Valutare la corrente totale
con il suo errore.
i1= __________±_____ A
i2= __________±_____ A
i= __________±_____ A
Confrontare i valori attesi con i valori
osservati. Che cosa notate?
3 Misura di tensione in un partitore di tensione
a. Resistenze da 1 KΩ
R1= __________±_____Ω
Misurare con il multimetro i valori di due
resistenze R1 e R2 da 1 KΩ .
Valutare quale deve essere la tensione
massima applicabile alle due resistenze
quando connesse in serie, ipotizzando
Pk<0.25 W. Valutare anche l’errore
relativo a tale misura. Non applicare
tensioni maggiori di detto valore. Se la
resistenza fosse maggiore, la tensione
massima applicabile sarebbe maggiore o
minore? Perché?
Determinare i valori attesi delle cadute di
tensione sulle tre resistenze, e la corrente
attesa nel circuito.
R2= __________±_____Ω
Vmax= __________±_____ V
V1= __________±_____V
V2= __________±_____V
9
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
i= __________±_____A
Misurare la tensione fornita al circuito e le
d.d.p. sulle due resistenze (queste ultime
contemporaneamente). Determinare la
corrente circolante nel circuito.
V1= __________±_____V
V2= __________±_____V
i= __________±_____A
Confrontare i valori attesi con i valori
osservati. Che cosa si nota?
a. Resistenze da 1 KΩ
R1= __________±_____Ω
Misurare con il multimetro i valori di due
resistenze R1 e R2 da 1 KΩ .
Valutare quale deve essere la tensione
massima applicabile alle due resistenze
quando connesse in serie, ipotizzando
Pk<0.25 W. Valutare anche l’errore
relativo a tale misura. Non applicare
tensioni maggiori di detto valore. Se la
resistenza fosse maggiore, la tensione
massima applicabile sarebbe maggiore o
minore? Perché?
R2= __________±_____Ω
Vmax= __________±_____ V
V1= __________±_____V
Determinare i valori attesi delle cadute di
tensione sulle tre resistenze, e la corrente
attesa nel circuito.
V2= __________±_____V
i= __________±_____A
Misurare la tensione fornita al circuito e le
d.d.p. sulle due resistenze (queste ultime
contemporaneamente). Determinare la
corrente circolante nel circuito.
V1= __________±_____V
V2= __________±_____V
i= __________±_____A
Confrontare i valori attesi con i valori
osservati. Che cosa si nota?
10
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
b. Resistenze da 1 MΩ
R1= __________±_____Ω
Misurare con il multimetro i valori di due
resistenze R1 e R2 da 1 MΩ .
Valutare quale deve essere la tensione
massima applicabile alle due resistenze
quando connesse in serie, ipotizzando
Pk<0.25 W. Valutare anche l’errore
relativo a tale misura. Non applicare
tensioni maggiori di detto valore.
R2= __________±_____Ω
Vmax= __________±_____ V
V1= __________±_____V
Determinare i valori attesi delle cadute di
tensione sulle tre resistenze, e la corrente
attesa nel circuito.
V2= __________±_____V
i= __________±_____A
Misurare la tensione fornita al circuito e le
d.d.p. sulle due resistenze (queste ultime
contemporaneamente). Determinare la
corrente circolante nel circuito.
V1= __________±_____V
V2= __________±_____V
i= __________±_____A
Confrontare i valori attesi con i valori
osservati. Che cosa si nota?
Determinare dalle ultime misure effettuate
il valore della resistenza interna del
multimetro usato come voltmetro.
R2v= __________±_____Ω
Rv= __________±_____Ω
4 Verifica della legge di Ohm
Misurare con il multimetro i valori esatti
R= __________±_____Ω
della resistenza R=1 MΩ .
Perché in questo caso non viene richiesto
di valutare la tensione massima applicabile
affinché non si brucino le resistenze?
Misurare 15 coppie di valori tensione- Tensione erogata Tensione su R
Corrente in R
corrente, facendo variare la tensione
1V
______±_____V ______±______
erogata dal generatore da 1 V a 15 V, e
2V
______±_____V ______±______
riportando per ogni misura l’errore
3V
______±_____V ______±______
relativo (ricordare che l’errore associato
4V
______±_____V ______±______
ad una misura è il minimo tra lo 0.3% e
5V
______±_____V ______±______
comunque non meno di 1 unità sulla cifra
6V
______±_____V ______±______
meno significativa);
11
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
meno significativa);
7V
8V
9V
10 V
11 V
12 V
13 V
14 V
15 V
Valutare il valore della resistenza R come
pendenza della retta di regressione y=Bx
usando il metodo dei minimi quadrati e
forzando a zero l’intercetta A; ricordare
che l’errore associato alla determinazione
N
di B è σ B = σ y
dove N è il numero di
∆
misure,
1
( yi − Bxi )2
∑
N i=1
sulla misura di y,
N
N
∆ = N ∑ xi2 − ∑ xi ;
i =1
i=1
N
B=
i =1
N
∑
∆= ____________________
σy= ____________________
è
e
2
N ∑ xi yi −
______±______
______±______
______±______
______±______
______±______
______±______
______±______
______±______
______±______
N
σy =
l’incertezza
______±_____V
______±_____V
______±_____V
______±_____V
______±_____V
______±_____V
______±_____V
______±_____V
______±_____V
invece
σB= ____________________
N
xi ∑ yi
i =1
i =1
(conviene
∆
effettuare tutti i conti con le funzioni di
Excel).
B= _________________±___________
Confrontare i valori ottenuti con il valore
vero di R.
12
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
Esperienza 3 - Circuiti in corrente alternata
Studenti presenti (firme): __________________________________________________________________
1 Misure su un circuito RC come filtro passa-basso
Prendere un resistore da 1 KΩ e un
condensatore da 680 nF, e
misurare i valori effettivi di R e C.
In assenza di tali componenti,
selezionarne altri che portino ad un
valore di τC simile a quello di
partenza.
Stimare la costante di tempo
τC=RC, la frequenza di taglio a 3
dB f0=ω 0/2π usando i valori
misurati di R e C.
Valutare graficamente la frequenza
di taglio f0 empirica.
R = __________±________Ω
C = __________±________nF
τC = __________±________
f0 = __________±________
ω 0 = __________±________
f0 = __________±________
2 Misure su un circuito RC come filtro passa-alto
Prendere un resistore da 1 KΩ e un
condensatore da 680 nF, e
misurare i valori effettivi di R e C.
Stimare la frequenza di taglio a 3
dB f0=ω 0/2π usando i valori
misurati di R e C.
Valutare graficamente la frequenza
di taglio f0 empirica.
R = __________±________Ω
C = __________±________nF
f0 = __________±________
ω 0 = __________±________
f0 = __________±________
Commentare i risultati ottenuti nei due casi.
13
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
Misure relative al circuito RC passa basso
Rilevare le tensioni picco-picco di vin(t) e vC(t) e la fase di vC(t) rispetto a vin(t), con i rispettivi errori di m
maggiori della frequenza di taglio a 3 dB f0 (prendere circa 15 misure, infittite intorno al valore di f0); ricord
gradi (o in radianti): tenendo conto che in realtà si misura il tempo di sfasamento ∆t, lo sfasamento angolare
temporale ∆t al periodo T e moltiplicandolo per l’angolo giro (360° o 2π), cioè ϕ = 360 ∆t / T;
Tensione
piccoTensione
Tensione
Tensione
Sfasamento Sfasamento Sfasamento
picco
picco-picco
picco-picco
picco-picco
Mis. Frequenza
su
C
di
Atteso
(div)
(°)
su C
di ingresso
(div)
ingresso
(div)
1
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
2
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
3
____
____±___
____±0.2 ____±___
____±0.2
____±0.2
____±___
4
____
____±___
____±0.2 ____±___
____±0.2
____±0.2
____±___
5
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
6
____
____±___
____±0.2 ____±___
____±0.2
____±0.2
____±___
7
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
8
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
9
____
____±___
____±0.2 ____±___
____±0.2
____±0.2
____±___
10
____
____±___
____±0.2 ____±___
____±0.2
____±0.2
____±___
11
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
12
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
13
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
14
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
15
____
____±___
____±0.2 ____±___
____±0.2
____±0.2
____±___
Commenti:
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
Misure relative al circuito RC passa alto
Rilevare le tensioni picco-picco di vin(t) e vC(t) e la fase di vC(t) rispetto a vin(t), con i rispettivi errori di m
maggiori della frequenza di taglio a 3 dB f0 (prendere circa 15 misure, infittite intorno al valore di f0); ricord
gradi (o in radianti): tenendo conto che in realtà si misura il tempo di sfasamento ∆t, lo sfasamento angolare
temporale ∆t al periodo T e moltiplicandolo per l’angolo giro (360° o 2π), cioè ϕ = 360 ∆t / T.
Tensione
piccoTensione
Tensione
Tensione
Sfasamento Sfasamento Sfasamento
picco
picco-picco
picco-picco
Mis. Frequenza
picco-picco
su
C
Atteso
(div)
(°)
di
su C
di ingresso
(div)
ingresso
(div)
1
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
2
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
3
____
____±___
____±0.2 ____±___
____±0.2
____±0.2
____±___
4
____
____±___
____±0.2 ____±___
____±0.2
____±0.2
____±___
5
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
6
____
____±___
____±0.2 ____±___
____±0.2
____±0.2
____±___
7
____
____±___
____±0.2 ____±___
____±0.2
____±0.2
____±___
8
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
9
____
____±___
____±0.2 ____±___
____±0.2
____±0.2
____±___
10
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
11
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
12
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
13
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
14
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
15
____
____±0.2
____±___
____±0.2 ____±___
____±0.2
____±___
Commenti:
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
Esperienza 4 - Indice di rifrazione ed aberrazioni
Studenti presenti (firme): __________________________________________________________________
1 Indice di rifrazione
Misura
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Media
Angolo di incidenza
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
Angolo di rifrazione
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
Indice di rifrazione
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
________±________
2a Aberrazione: misure con lastra di plexiglass
∆x
∆y
2b Aberrazione: misure con specchietto metallico
∆x
∆y
16
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
17
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
18
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
19
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
Esperienza 5 – Lunghezza focale delle lenti
Studenti presenti (firme): __________________________________________________________________
1 Misure con la prima lente convergente
Posizione sorgente: ________±_______
Riportare le posizioni e le dimensioni della sorgente
(reticolo illuminato dalla lampada), che non dovrà
essere mossa durante tutta l’esperienza.
Dimensioni sorgente: ________±_______
2 Misure con la seconda lente convergente
Riportare le posizioni e le dimensioni della sorgente Posizione sorgente: ________±_______
(reticolo illuminato dalla lampada), che non dovrà
essere mossa durante tutta l’esperienza.
Dimensioni sorgente: ________±_______
3 Misure con il sistema di due lenti
Riportare le posizioni e le dimensioni della sorgente Posizione sorgente: ________±_______
(reticolo illuminato dalla lampada), che non dovrà
essere mossa durante tutta l’esperienza.
Dimensioni sorgente: ________±_______
21
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
1 Misure con la prima lente convergente
Inserire i Confrontare
Numero
misura
Misura
posizione
lente
Misura
posizione
immagine
Misura
dimensioni
immagine
Calcolo
Valore
ingrandimento
distanza tra
da misure
oggetto e lente
(M=l’/l)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Media
Confrontare il valore medio ottenuto per la distanza focale con il valore atteso.
Valor
distanza
immagin
lente
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
2 Misure con la seconda lente convergente
Numero
misura
Misura
posizione
lente
Misura
posizione
immagine
Misura
dimensioni
immagine
Calcolo
Valore
ingrandimento
distanza tra
da misure
oggetto e lente
(M=l’/l)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Media
Confrontare il valore medio ottenuto per la distanza focale con il valore atteso.
Valor
distanza
immagin
lente
Calcolo distanza
tra prima lente ed
Misura distanza
tra seconda lente
ed immagine (s2’)
Misura distanza
tra oggetto e
prima lente (s1)
Calcolo distanza
tra le lenti (L)
Calcolo
ingrandimento da
misure (M=l’/l)
Misura
dimensione
immagine
Misura posizione
schermo
Misura posizione
lente convergente
Misura posizione
lente divergente
Numero misura
Università degli Studi di Torino – C.S. Chimica – Corso di Fisica C – A.A. 2002-2003
3 Misure con il sistema di due lenti (convergente e divergente)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Commentare le misure ottenute (tipi di immagini – se reali o virtuali, se dritte o rovesciate - , ingrandimenti, ecc