RELAZIONE LABORATORIO DI MISURE
4-6-03
OGGETTO:
Misura dello sfasamento tra INGRESSO e USCITA di un circuito RC, al variare della frequenza
dell’ingresso, quando in ingresso è posta una tensione sinusoidale di ampiezza 20V picco-picco:
R
A1
C
A2
Tracciamento del diagramma di Bode delle fasi per questo filtro RC.
STRUMENTAZIONI UTILIZZATE:
- un generatore di tensione AGILENT 33120A, n° di serie MY40013665;
- un oscilloscopio TEKTRONIX modello TDS210 n° serie B011863;
DESCRIZIONE DEL PROCEDIMENTO
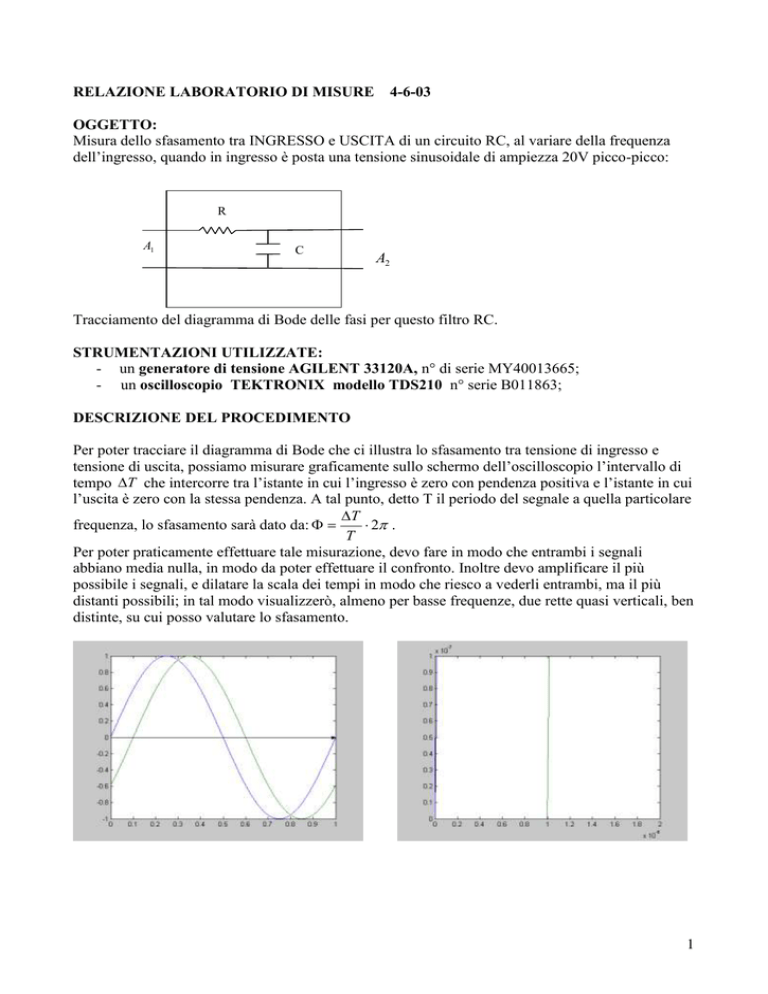
Per poter tracciare il diagramma di Bode che ci illustra lo sfasamento tra tensione di ingresso e
tensione di uscita, possiamo misurare graficamente sullo schermo dell’oscilloscopio l’intervallo di
tempo T che intercorre tra l’istante in cui l’ingresso è zero con pendenza positiva e l’istante in cui
l’uscita è zero con la stessa pendenza. A tal punto, detto T il periodo del segnale a quella particolare
T
2 .
frequenza, lo sfasamento sarà dato da:
T
Per poter praticamente effettuare tale misurazione, devo fare in modo che entrambi i segnali
abbiano media nulla, in modo da poter effettuare il confronto. Inoltre devo amplificare il più
possibile i segnali, e dilatare la scala dei tempi in modo che riesco a vederli entrambi, ma il più
distanti possibili; in tal modo visualizzerò, almeno per basse frequenze, due rette quasi verticali, ben
distinte, su cui posso valutare lo sfasamento.
1
ESECUZIONE DELLA MISURA.
Impostiamo il generatore di segnali, in modo da ottenere l’ingresso desiderato:
Vpp 20V
Out Terms: High Z (Alta impedenza)
Iniziamo a lavorare per f 10 Hz , poi aumentiamo di volta in volta la frequenza con passo di 10
Hz. Per ogni frequenza individueremo inoltre la migliore configurazione dei secondi per divisione,
mentre utilizzeremo sempre, sull’asse delle y, 2 mV/div.
Nella tabella seguente riportiamo il valore dello sfasamento al variare della frequenza.
FREQUENZA
F [Hz]
10
100
1 10 3
1 10 4
1 10 5
1 10 6
PERIODO
T [s]
0.1
0.01
0.001
0.0001
0.00001
0.000001
[s/div]
50 s / div
25 s / div
25 s / div
2.5 s / div
250 ns / div
50 ns / div
Divisioni di
differenza
5
7.7
5.2
8.6
8.1
2
T
250
192
130
21.5
2.07
100
T
2
T
0.015 rad
0.12 rad
0.82 rad
1.35 rad
1.3
rad
0.63 rad
s
s
s
s
s
ns
Notiamo che lo sfasamento aumenta finchè le frequenze si mantengono su valori non troppo alti
(senza peraltro superare il valore di 90°); per frequenze superiori ai 100 KHz incominciano ad avere
sempre più peso gli effetti capacitivi ed induttivi di R e gli effetti dissipativi di C.
In pratica il modello usato fino ad ora non va più bene, e deve essere sostituito con uno del tipo:
Fino ad ora non abbiamo utilizzato il nostro oscilloscopio con tutte le funzioni; ne abbiamo
utilizzati la parte “analogica”, mentre ci sarebbe stato possibile leggere i valori di misura tramite dei
cursori che ci avrebbero restituito il valore numerico da noi cercato; in particolare per una frequenza
di 1000 Hz, con una risoluzione di 25 s / div , sovrapponendo i cursori sui segnali l’oscilloscopio
2
ci restituisce direttamente il valore di T 131s . La risoluzione con cui si spostano i cursori, nel
s / div
caso di 25 s / div , è di 1 s . In generale risoluzion e
.
25
Un’altra funzione dell’oscilloscopio è quella per cui riesco ad abbattere il rumore di un segnale,
facendo una media su varie misurazioni.
VALUTAZIONE DELL’INCERTEZZA
Categoria A.
Se la andassimo a valutare ci verrebbe nulla; ma noi sappiamo che non esiste una misurazione priva
di incertezza; il problema è legato alla risoluzione: noi ci affidiamo all’occhio umano, che può
percepire al massimo un decimo della divisione; tale risoluzione è insufficiente: anche se mi rendo
conto che le misure variano, il fatto che l’incertezza è inferiore alla risoluzione, mi fa apparire
uguali tutte le misure che dovrei mediare.
Categoria B
Essa è presente in quanto l’oscilloscopio non è ideale; la riesco a valutare tramite il manuale, che mi
fornisce le varie incertezze.
Qualora una misurazione non restituisca un valore accettabile o contraddittorio, devo calibrare lo
strumento.
Infine, nel dominio del tempo, l’oscilloscopio può essere usato anche per determinare la costante di
tempo del circuito RC; consideriamo ad esempio in ingresso un’onda quadra a 100 Hz, con 20 Vpp;
la costante di tempo è data dal tempo che impiega la tangente alla curva di uscita per raggiungere il
valore di 20 V.
Ponendo CH1= 500 mV/div e M=10 s / div , riesco a vedere che raggiunge i 20 volt in 200s .
1
Questa è proprio la costante RC; come verifica ricaviamo tale costante dalla relazione: f T
;
2RC
sapendo che f T 814Hz , trovo RC 196 s .
3