Chimica Fisica 2
chimica industriale 2°anno
A.A. 2009-10
NMR
Antonio
Toffoletti
Momento di spin dei nuclei
Numero di massa
dispari
pari
I=n/2
1H
I=1/2
13C
23Na
.....
I=1/2
I=3/2
I=n
dispari
I=0
pari
2H
I=1
12C
I=0
14N
I=1
16O
I=0
.....
.....
Numero atomico
Risonanza
magnetica
di spin
nucleare
Radiofrequenze: per esempio
ν = 600 MHz B = 14 T
= 14’000 Gauss
(EPR : ν = 9500 MHz B = 0.35 T)
= 3’500 Gauss)
Il momento magnetico dei nuclei è proporzionale al loro
momento angolare di spin. Si può definire la proporzionalità
usando due diverse costanti:
e
µN =
= 5.051×10 − 27 JT −1 magnetone di
Bohr nucleare
2 mH
gN e
γ=
2mH
rapporto
giromagnetico
carica
dell’elettrone
fattore g
nucleare
(numero)
µI = gN µN I
massa
del H
µ I = γI
Il momento magnetico di spin
nucleare si può scrivere usando le
due notazioni:
Componenti del momento magnetico
nucleare lungo una direzione z
I nuclei studiati più spesso sono 1H e 13C che
hanno spin I=1/2
Le funzioni di spin nucleare sono:
ψα e ψβ vengono indicate semplicemente con
α e β
Se I=1/2:
I z ψ α = 1 2ψ α
I z ψ β = − 1 2ψ β
µI = 1 2 gN µN
z
µI = −1 2 gN µN
z
oppure
Iz α = 1 2α
mI = 1 2
Iz β = − 1 2 β
mI = − 1 2
In generale:
µ I = g N µ N mI
z
Nucleo
Abbondanz
a naturale
Spin
gN
1H
99.98 1/2
5.586
2H
0.02
1
0.857
13C
1.11
1/2
1.405
14N
99.64 1
0.404
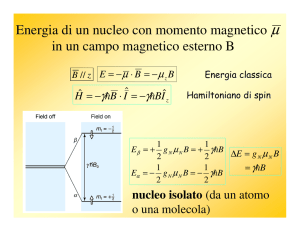
Energia di un nucleo con momento magnetico µ
in un campo magnetico esterno B
B // z E = − µ ⋅ B = − µ z B
Hˆ = −γB ⋅ Iˆ = −γBIˆz
Energia classica
Hamiltoniano di spin
1
1
Eβ = + g N µ N B = + γB ∆E = g µ B
N N
2
2
1
1
= γB
Eα = − g N µ N B = − γB
2
2
nucleo isolato (da un atomo
o una molecola)
Frequenza di Larmor di un nucleo con
momento magnetico µ
Le energie dei nuclei si esprimono spesso in funzione della
frequenza νL detta Frequenza di Larmor
γ
νL =
B
2π
1
1
1
Eβ = + g N µ N B = + γB = + hν L
2
2
2
1
1
1
Eα = − g N µ N B = − γB = − hν L
2
2
2
∆E = g N µ N B
Condizione di risonanza
= γB
= hν L
hν = ∆E = hν L
Hamiltoniano di spin per i momenti nucleari
in una molecola (o in un atomo) - 1
Nucleo “nudo”
elettroni
B
H
δB
Bloc = B + δB
= (1 − σ )B
Nucleo in una
molecola (o in
un atomo)
δB = −σB
Hˆ = −γB ⋅ Iˆ = −γBIˆz
Hˆ = −γ ( B + δB ) Iˆz
Hˆ = −γ(1 − σ ) BIˆz
σ Costante di schermo
Il campo magnetico che agisce sul nucleo in una molecola è
il campo locale Bloc dato dalla composizione del campo
esterno B e di un campo aggiuntivo δB dovuto al contributo
elettronico.
Hamiltoniano di spin per i momenti nucleari
in una molecola (o in un atomo) - 2
elettroni
B
H
Nucleo in una
molecola (o in
un atomo)
Hˆ = −γ(1 − σ ) BIˆz
δB
δB = −σB
Bloc = B + δB
= (1 − σ )B
σ Costante di schermo
Per il nucleo in una molecola (o in un atomo)
la frequenza di Larmor è definita da:
(ν L )i
γi
γi
(1 − σ i )B
=
Bloc =
2π
2π
Frequenza di risonanza dei nuclei
in una molecola (o in un atomo)
Condizione di risonanza
hν = ∆E
hν = γ(1 − σ ) B
∆E = γ(1 − σ ) B
= hν L
= hν L
ν =νL
Frequenze degli
spettrometri NMR
ν
B0
400 MHz
9.6 T
500 MHz
12 T
600 MHz
14.4 T
900 MHZ
21.6 T
Spostamento chimico
(Chemical Shift)
La frequenza di risonanza dei nuclei si può misurare come distanza da
quella di uno standard :
∆ν
ν
ν0
Standard
Svantaggio: ∆ν dipende dalla frequenza
di lavoro, è difficile confrontare risultati
ottenuti con spettrometri diversi
Si preferisce quindi usare un parametro adimensionale
(spostamento chimico) dato da:
ν −ν 0
δ=
×106
ν0
δ
0
Standard
δ non dipende dalla frequenza di lavoro
δ > 0 significa ν > ν 0
Il campo locale che agisce sul nucleo
è maggiore di quello dello standard.
Il nucleo è meno schermato dello standard
La differenza tra l’ordine di grandezza degli spostamenti chimici
chimici dei protoni e di
13
quelli dei nuclei di C è dovuta alla maggiore densità elettronica che circonda
questi ultimi.
Accoppiamento di Fermi o di contatto
tra spin dell’elettrone (S) e spin del nucleo (I)
Introduciamo ora una interazione magnetica tra i momenti di spin
dell’elettrone e del nucleo nota come interazione “di contatto” o “di
Fermi”.
Se un elettrone in un atomo o in una molecola è descritto da una funzione
d’onda che ha una probabilità diversa da zero di trovarsi su un nucleo
dotato di spin, allora tra i due momenti ci sarà un “accoppiamento”, cioè
l’energia sarà diversa a seconda dell’orientazione reciproca degli spin
dell’elettrone ms e del nucleo mI.
H Fermi = aSz I z
EFermi = ams mI
a si chiama “costante di accoppiamento iperfine” elettrone-nucleo. La
ritroveremo nella spettroscopia ESR (EPR).
Accoppiamento
spin-spin
Ac
tra spin del nucleo 1 (I1) e spin del nucleo 2 (I2)
H Fermi = aSz I z
EFermi = ams mI
Consideriamo
come esempio la
molecola di H2
spin
dell’elettrone
spin del
protone
1. L’accoppiamento di Fermi
favorisce energeticamente la
interazione di un elettrone con spin
α con un nucleo con spin β, e
viceversa.
2. Quindi sarà più probabile
trovare l’elettrone con spin α
vicino e sul nucleo con spin β,
come indicato simbolicamente in
figura.
3. Corrispondentemente sull’altro
nucleo ci sarà una piccola
preponderanza di elettrone con
spin β. Se questo secondo nucleo
ha spin α ci sarà un ulteriore
abbassamento dell’energia,
sempre a causa dell’interazione di
Fermi.
4. Viceversa se questo secondo
nucleo ha spin β, l’interazione di
Fermi alzerà l’energia.
5. Quindi in questo caso abbiamo
un bilancio energetico più
sfavorevole del precedente.
6. Quindi in conclusione l’energia
sarà più bassa se i due nuclei
hanno spin opposto, più alta se
hanno lo stesso spin.
7. Questo si può tradurre in un
“hamiltoniano di spin nucleare”,
cioè che contiene solo operatori
che agiscono sullo spin nucleare:
H acc = J I z1 I z2
Eacc = J mI1 mI 2
E
8. La costante di accoppiamento
spin-spin J (espressa in unità di
frequenza) è dell’ordine degli Hz:
l’energia in gioco è piccolissima
rispetto alle energie degli stati
elettronici (≈1015 Hz). La
costante può essere positiva o
negativa a seconda del numero e
tipo di legami chimici che
separano i due nuclei.
Hamiltoniano di spin in funzione della
frequenza
h
ˆ
H = −γ i
(1 − σ i ) BIˆzi
2π
γi
Hˆ
=−
(1 − σ i ) BIˆzi
h
2π
= −ν L i Iˆzi
Frequenza di Larmor del nucleo i-esimo
(ν L )i
γi
γi
(1 − σ i )B
=
Bloc =
2π
2π
Spettro NMR di due protoni accoppiati
e con lo stesso chemical shift
H = −νI1 − νI 2 + JI1 I 2
Tutte le transizioni corrispondono
alla stessa frequenza di risonanza.
ν
L’accoppiamento all’interno di gruppi equivalenti di
protoni non si manifesta nello spettro
Spettro NMR di due protoni accoppiati con chemical
shift diverso
H = −ν 1I z1 −ν 2 I z 2 + JI z1I z 2
E = −ν 1mI1 −ν 2 mI 2 + JmI1mI 2
ββ
∆E = ν 1 +
1
J
2
½ ν1 + ½ ν2 + 1/4J
∆E = ν 2 +
-½ ν1 +½ ν2 - 1/4J
½ ν1 - ½ ν2 - 1/4J
βα
αβ
∆E = ν 1 −
1
J
2
1
J
2
∆E = ν 2 −
αα
1
J
2
-½ ν1 - ½ ν2 + 1/4J
ν1
ν2
Accoppiamento tra gruppi di nuclei
ν A ,ν B
3 nuclei A
equivalenti
2 nuclei B
equivalenti
frequenze di risonanza
NMR
Se tra i due gruppi di nuclei non
ci fosse accoppiamento...
νA
νB
Ma se c’è accoppiamento i nuclei A risentono della
situazione dei nuclei B, e viceversa. In tal caso ogni riga
dovuta ad un gruppo di nuclei equivalenti si separa (splitting)
in un numero di righe corrispondente ai diversi stati di spin
del gruppo vicino.
3 nuclei A
equivalenti
2 nuclei B
equivalenti
νA
J=0
νB
3 : 2
Gli integrali
dei due
multipletti
stanno nello
stesso
rapporto del
numero di
protoni
equivalenti
corrispondenti
J≠0
J
1
J
2
J
1
Tripletto di righe
1
J
3
J
3
Quartetto di righe
1
OH
CH2
il protone dell’OH è ancora
meno schermato. Qui
scambia “rapidamente” con
le altre molecole ed è quindi
disaccoppiato dagli altri
nuclei
I protoni del metilene sono
meno schermati di quelli
del metile (δ più grande).
Quartetto 1:3:3:1 per
accoppiamento con il CH3
Integrali dei multipletti. Sono
proporzionali al numero di
nuclei che contribuiscono al
multipletto.
CH3
Tripletto 1:2:1 per
accoppiamento con
il CH2
Multipletti di righe NMR
L’accoppiamento all’interno di ogni gruppo di protoni
equivalenti non si manifesta nello spettro.
La risonanza di ogni gruppo è invece separata in più righe
dall’accoppiamento con gruppi di altri protoni.
L’accoppiamento con un gruppo di n protoni equivalenti separa
la risonanza in n+1 righe equidistanti le cui intensità relative
sono date dal triangolo di Tartaglia.
numero di H
Numero e intensità delle righe
0
1
1
1
1
2
1
3
1
4
5
1
2
3
4
5
1
1
3
6
10
1
4
10
1
5
1
ecc.