grafi-29-3-04.nb
1
II modulo A: funzione f x
Dominio: 1
x
1.
x3
Quindi D f
Log 1
0, ovvero x3
1,
x3
1, ovvero
.
Segno: f x 0 se e solo se 1 x3 1, ovvero se e
solo se x3 0, ovvero se e solo se x 0.
Inoltre, f 0
Log 1
0, f x
0 se x
Abbiamo
limx
f x
limx
limx
Log x3
Inoltre, poiché 1
limx
1
f x
x3
limx
Log 1 x3
3 limx
Log x
0 abbiamo anche
1
Log 1
x3
1, 0 .
grafi-29-3-04.nb
2
La derivata:
3 x2
1 x3
f' x
0
x
0 nel dominio.
Quindi f ha un solo intervallo di monotonia (è
crescente su 1,
).
Inoltre il grafico ha tangente orizzontale in x 0.
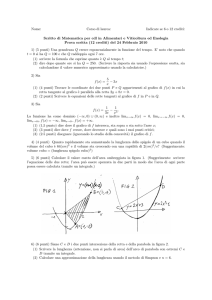
ParametricPlot
t, Log 1
t^3
, t,
1, 8
6
4
2
2
4
6
8
-2
-4
Graphics
II modulo B: funzione f x
Dominio: D f
Funzione pari.
Segno:
, 1
x2 1
x2 1
1, 1
1,
.
grafi-29-3-04.nb
se x2
x2 1
ovvero
x
retta y
3
1 0 , dividendo la diseguaglianza
x2 1
2
2
x 1per x 1 0 otteniamo x2 1 1,
f x 1. Quindi la porzione del grafico per
, 1
1,
giace al di sopra della
1.
Se invece x2 1 0, dividendo la diesguaglianza
x2 1 1 x2 per 1 x2 0 otteniamo l'altra
f x 1 ovvero 1 f x . Quindi la porzione
del grafico per x
1, 1 giace al di sotto della
1. Si ha f 0
1.
retta y
Limiti agli estremi:
limx
f x
x2
x2
limx
1.
Per x che tende a 1 da destra e da sinistra:
limx
1
f x
limx
1
2
2 x 1
grafi-29-3-04.nb
limx
1
4
f x
limx
1
2
2 x 1
Si scriva x 1
con
0 nel primo caso,
con
0 nel secondo
x 1
e si prenda il limite per
0 .
Derivata prima:
f' x
4x
x2 1
2
.
Quindi f x 0 per ogni x 0 nel dominio,
f ' 0 0, f ' x 0 per ogni x 0 nel dominio.
Pertanto, f ha quattro intervalli di monotonia:
, 1,
1, 0 ove f è crescente,
0, 1 , 1,
ove f è decrescente.
ParametricPlot
t, t ^ 2
1
t^2
1
, t,
10, 10
grafi-29-3-04.nb
5
10
5
-5
-2.5
2.5
-5
-10
Graphics
5
7.5
10