Campo magnetico di un filo conduttore, rettilineo ed infinitamente lungo, percorso da corrente
elettrica
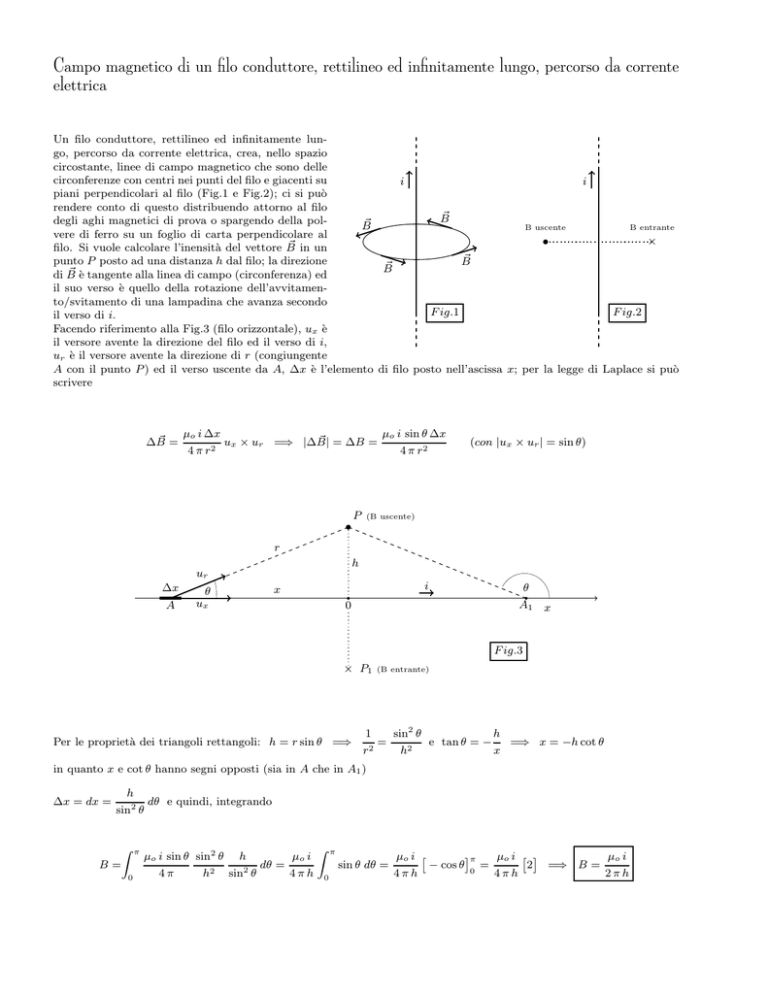
Un filo conduttore, rettilineo ed infinitamente lungo, percorso da corrente elettrica, crea, nello spazio
circostante, linee di campo magnetico che sono delle
circonferenze con centri nei punti del filo e giacenti su
i
i
piani perpendicolari al filo (Fig.1 e Fig.2); ci si può
rendere conto di questo distribuendo attorno al filo
~
B
degli aghi magnetici di prova o spargendo della pol~
B
B uscente
B entrante
vere di ferro su un foglio di carta perpendicolare al
×
~ in un
filo. Si vuole calcolare l’inensità del vettore B
~
punto P posto ad una distanza h dal filo; la direzione
B
~
B
~ è tangente alla linea di campo (circonferenza) ed
di B
il suo verso è quello della rotazione dell’avvitamento/svitamento di una lampadina che avanza secondo
F ig.1
F ig.2
il verso di i.
Facendo riferimento alla Fig.3 (filo orizzontale), ux è
il versore avente la direzione del filo ed il verso di i,
ur è il versore avente la direzione di r (congiungente
A con il punto P ) ed il verso uscente da A, ∆x è l’elemento di filo posto nell’ascissa x; per la legge di Laplace si può
scrivere
~ =
∆B
µo i ∆x
4 π r2
~ = ∆B =
ux × ur =⇒ |∆B|
P
µo i sin θ ∆x
4 π r2
(con |ux × ur | = sin θ)
(B uscente)
r
h
ur
∆x
A
i
x
θ
ux
θ
A1
0
x
F ig.3
× P1
Per le proprietà dei triangoli rettangoli: h = r sin θ =⇒
1
r2
(B entrante)
=
sin2 θ
h2
e tan θ = −
h
x
=⇒ x = −h cot θ
in quanto x e cot θ hanno segni opposti (sia in A che in A1 )
∆x = dx =
h
sin2 θ
B=
Z
0
π
dθ e quindi, integrando
µo i sin θ sin2 θ
4π
h2
h
2
sin θ
dθ =
µo i
4πh
Z
0
π
sin θ dθ =
µo i 4πh
− cos θ
π
0
=
µo i µo i
2 =⇒ B =
2πh
4πh












