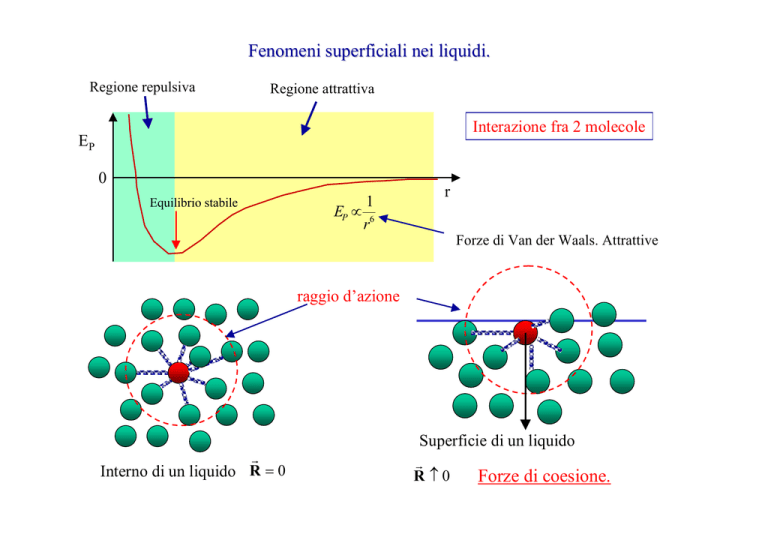
Fenomeni superficiali nei liquidi.
Regione repulsiva
Regione attrattiva
Interazione fra 2 molecole
EP
0
Equilibrio stabile
1
EP ∝ 6
r
r
Forze di Van der Waals. Attrattive
raggio d’azione
r
Interno di un liquido R = 0
Superficie di un liquido
r
R≠0
Forze di coesione.
Fenomeni superficiali nei liquidi
l
lato mobile: tirato
verso l’interno
F = 2τ l
[τ ] =
N
m
rompendo la lamina
tensione superficiale. forza per unità di lunghezza
τ (>0) è una proprietà del liquido; diminuisce con la temperatura;
dipende dal materiale con cui è a contatto
Due facce
dx
/ = F ⋅ dx = 2τ l dx
Lavoro della forza esterna F in uno spostamento dx:
F
l
/ = ∆W ⇒
/ = 2τ dS
τ : energia per unità di superficie
W =τ S
superficie totale
L’equilibrio stabile corrisponde a W minima
a un liquido tende rendere minima
la sua superficie libera. Es. gocce sferiche.
A contatto con aria, a 20°C
τ = 0.072 N/m
Acqua :
Alcool etilico: τ = 0.022 N/m
τ = 0.465 N/m
Mercurio:
Fenomeni superficiali nei liquidi.
Liquido a contatto con un solido (o altro liquido non miscibile)
Solido. Adesione
Adesione > Coesione. Liquido bagna.
Liquido. Coesione
Adesione < Coesione. Il liquido non bagna.
τ2
τ1
τ3
olio
in equilibrio:
r
r
r
τ 1dl + τ 2 dl + τ 3 dl = 0
Se l’acqua è pura τ1 è maggiore. L’olio si espande.
Descrizione in termini di energia
W = τ 1 S Aa + τ 2 S Oa + τ 3 S OA
minima.
Legge di Laplace
Per una goccia:
Pe: pressione esterna; Peπr2
Pi: pressione interna; Piπr2
T: tensione superficiale; 2πrτ
pi − pe =
2τ
r
Per una bolla (2 superfici):
pi − pe =
p maggiore
p minore
Dimostrazione per una goccia (1 superficie)
d / = ∆ p ⋅ dV = 4 π R 2 dR ∆ p
d / = τ dS = 8 π RdR τ
Lavoro contro le forze di pressione
Variazione di energia potenziale.
In alternativa:
In generale:
2 π r τ sin θ = F N
r = R sin θ
∆P =
e S = π r2
τ
τ
+
R1
R2
4τ
r
Fenomeni superficiali nei liquidi.
L’effetto di adesione e coesione si manifesta nella superficie libera dei liquidi: comparsa di un “menisco”
θθ
L’angolo di contatto dipende dal liquido e
dal solido utilizzati (e dalla temperatura).
θ
Data una combinazione liquido-solido
l’angolo ha un valore caratteristico.
insetto che cammina
sull’acqua
attrazione fra piccoli galleggianti.
perché il liquido
non scende?
Embolo
Fenomeni di capillarità
h =
2 τ cos α
ρ gr
Legge di Jurin per la
salita capillare
il liquido bagna
α < 90°, h > 0
P0
il liquido non bagna
α > 90°, h < 0
Legge di Laplace
B è immediatamente
sotto la superficie libera
PB = P0 −
2τ
2τ cos α
= P0 −
R
r
Legge di Stevino:
P0
P A = P B + ρ gh
ma PA = P0
Attenzione: r è il raggio del capillare, R il raggio di curvatura del menisco.
r = R cos α












