Il MOSFET (Metal Oxide Semiconductor Field Effect Transistor).
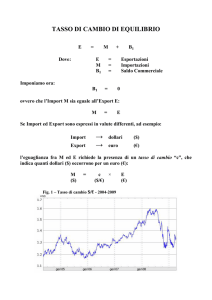
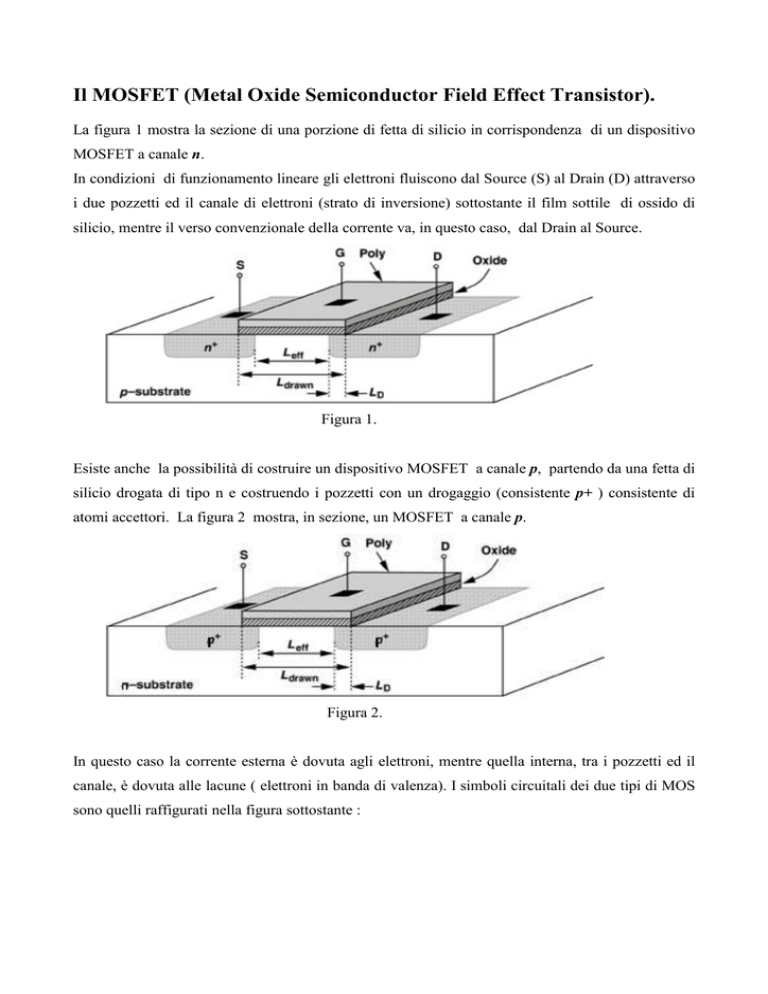
La figura 1 mostra la sezione di una porzione di fetta di silicio in corrispondenza di un dispositivo
MOSFET a canale n.
In condizioni di funzionamento lineare gli elettroni fluiscono dal Source (S) al Drain (D) attraverso
i due pozzetti ed il canale di elettroni (strato di inversione) sottostante il film sottile di ossido di
silicio, mentre il verso convenzionale della corrente va, in questo caso, dal Drain al Source.
Figura 1.
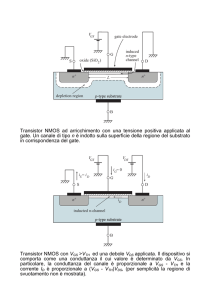
Esiste anche la possibilità di costruire un dispositivo MOSFET a canale p, partendo da una fetta di
silicio drogata di tipo n e costruendo i pozzetti con un drogaggio (consistente p+ ) consistente di
atomi accettori. La figura 2 mostra, in sezione, un MOSFET a canale p.
Figura 2.
In questo caso la corrente esterna è dovuta agli elettroni, mentre quella interna, tra i pozzetti ed il
canale, è dovuta alle lacune ( elettroni in banda di valenza). I simboli circuitali dei due tipi di MOS
sono quelli raffigurati nella figura sottostante :
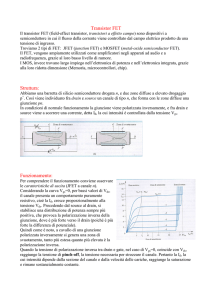
Le caratteristiche di uscita di un MOSFET a canale n sono rappresentate nella figura 3.
VGS rappresenta la tensione di gate.
Figura 3
In prima approssimazione tali caratteristiche sono descritte, nel primo tratto di tipo parabolico dalla
relazione semplificata
I DS = µ nCOX
VDS 2
W
V
V
V
−
−
(
)
G T DS
L
2
(1)
Dove µn = mobilità degli elettroni nel canale;
COX = Capacità dell’ossido di gate;
W = larghezza della regione di gate;
L = lunghezza della regione di gate;
VG = Tensione presente al gate;
VT = Tensione di soglia del MOS;
VDS = Tensione Drain -Source.
Nella regione di saturazione delle caratteristiche, in prima approssimazione, la corrente IDS è data
da:
I DS = µ nCOX
W
2
(VG − VT )
2L
(2)
In pratica questa regione è caratterizzata da rette non parallele all’asse IDS=0.
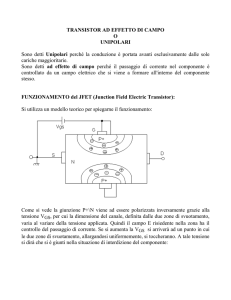
Figura 4. Configurazione Source Comune
Si consideri la configurazione circuitale a sorgente comune rappresentata nella figura 4, e per essa
cerchiamo di determinare il circuito equivalente per piccoli segnali, in regime lineare e di bassa
frequenza.
In questo contesto la corrente drain-source iD può essere espressa come funzione della tensione
gate-source vGS e drain-source vDS , cioè :
iD = F ( vGS , vDS )
(3)
Considerando incrementi finiti di vGS e vDS si può scrivere:
∆iD =
∂iD
∂vGS
∆vGS +
vDS
∂iD
∂vDS
∆vDS
(4)
vGS
che, considerando la notazione in uso per piccoli segnali, diventa
id =
∂iD
∂vGS
vgs +
vDS
∂iD
∂vDS
vds
(5)
vGS
Introducendo le seguenti definizioni:
gm =
Transconduttanza
∂iD
∂vGS
rds =
Resistenza differenziale di canale
iD
vgs
→
vDS
∂vDS
∂iD
→
vGS
vds
id
(6)
vds
(7)
vgs
allora la (5) si può scrivere come:
id = g m vgs +
vds
rds
(8)
Inoltre se definiamo µ, coefficiente di amplificazione del MOSFET, come:
µ=−
∂vDS
∂vgS
≅−
iD
vds
vgs
(9)
id
la (8) diventa
µ = g m rds
(10)
Ora siamo nelle condizioni di generare il circuito equivalente per piccoli segnali, per la
configurazione circuitale source comune.
La (8) si può scrivere, infatti:
0 = −id rds + g m v gs rds + vds
(11)
A cui corrisponde i circuiti di figura 5a, oppure il circuito di figura 6a
Figura 5b.
Circuito equivalente nella configurazione source
comune: rds=r0
Figura 5a.
Circuito equivalente generato dalla (11) dove
rds=r0
Utilizzando la (10) nella (11) si ottiene la condizione per generare un altro tipo di circuito
equivalente (figura 6 a e b) .Infatti dalla (11) e (10) si ha :
0 = −id rds + µ vgs + vds
(12)
Valutiamo il guadagno in tensione dal circuito equivalente di figura 5 b, cioè nel source comune :
Av =
vo − g m vgs ( rds * RL )
=
vi
vi ( rds + RL )
vgs =vi → Av =
− g m ( rds * RL )
( rds + RL )
(13)
Quindi:
Av = − g m RL
rds
a)
(14)
b)
Figura 6
a) Circuito equivalente generato dalla formula 12. b) Circuito equivalente della configurazione Source Comune
Esempio
g m = 30 ⋅10−3 mhos
4
rds = 10 Ω
4
R L = 10 Ω
Av = −
30*10 −3 *108
= −150
2*104
(15)
Il segno meno indica che il segnale in uscita è sfasato di 180° rispetto a quello presente in ingresso.
Il guadagno in potenza è teoricamente infinito e essendo pari a zero la potenza presente in ingresso.
Amplificatore a Drain Comune.
La configurazione a drain comune di un mosfet è mostrata in figura 7.
Figura 7
Per quanto attiene il circuito equivalente si consideri la figura 8 o anche la figura 9 dove si è passati
dal circuito equivalente di Norton a quello di Thevenin
Figura8
Figura 9
Dalla figura 9 si ha :
is =
g m vgs rds
Rs + rds
(16)
Poichè
vgs = vi − RS iS
(17)
si ha che :
RS g m rds vi RS 2 g m rds is
vo = iS RS =
−
=
RS + rds
RS + rds
R g r
is RS 1 + S m ds
RS + rds
A=
RS g m rds vi
=
RS + rds
RS + rds
vo RS g m rds
=
vi
RS + rds RS g m rds + RS + rds
(18)
Se rds>>RS allora
A≅
g m RS
<1
1 + g m RS
Se gm= 30*10-3 mho e RS=200Ω
20*10−3 * 200
A≅
= 0.8
1 + 20*10−3 * 200
(19)
Per quanto attiene l’impedenza d’uscita conviene trasformare il circuito di figura 9 in quello della
figura sottostante.
Si agisce applicando la tensione vo cortocircuitando il gate vgs= - vo e calcolando il rapporto tra vo
e –i2 :
i1rds + v0 g m rds + (i1 − i2 ) RS = 0
v0 + RS (i2 − i1 ) = 0
(20)
Risolvendo il sistema si ha:
Z0 =
v0
RS rds
1
=
= RS rds
−i2 RS g m rds + RS + rds
gm
(21)
Esempio
Se
RS = 100Ω
4
r ds = 10 Ω
−3
g m = 30*10 mho
Z0 =
102 *10 4
106
≅
= 25Ω
104 + 3*10−2 *106 + 100 4*104
Si noti che il segnale d’uscita in questa configurazione è in fase con quello d’ingresso ; l’impedenza
d’ingresso è alta , mentre l’impedenza d’uscita è piccola e minore della RS. Questo circuito può
essere impiegato come trasformatore d’impedenza (separatore).
Amplificatore a Gate Comune.
La configurazione di un MOSFET a gate comune e’ quella di figura 10.
Figura 10
Ed i circuiti equivalenti di Norton e Thevenin sono mostrati nelle figure 11a e 11b.
a)
b)
Figura 11
Dalla figura 11b si può scrivere:
iRL − vi + iRS + g m vgs rds + irds = 0
vgs = iRS − vi
(22)
da cui si ottiene
i=
vi (1 + g m rds )
RS g m rds + RS + rds + RL
(23)
Per quanto attiene l’impedenza d’ingresso si ha:
Zi =
v i RS g m rds + RS + rds + RL
=
i
1 + g m rds
Per quanto riguarda il guadagno di tensione, con uscita nel drain:
(24)
Av =
RL (1 + g m rds )
v0 iRL
=
=
vi
vi
RS g m rds + RS + rds + RL
(25)
Esempio
RL = 104 Ω
g m = 20*10−3 mho
rds = 10 4 ohm
RS = 100 ohm
Dalla 25 si ottiene
Av =
104 (1 + 20*10−3 *104 )
104 + 104 + (1 + 20*10−3 *104 )100
! 50
(26)
MOS COMPLEMENTARE
Figura 12
E’ costituito da due MOS (QP), uno a canale n, l’altro a canale p, connessi come in figura 12.
Per tensioni applicate in ingresso fino a Vγ (tensione di soglia d’ingresso) il canale formato è quello
del mos 1, pe rcui la tensione d’uscita è pari a vu=VDD. Non passa corrente nel canale di lacune.
Per tensioni applicate superiori a Vγ il canale formato e’ quello del MOS 2 (QN), per cui la tensione
d’uscita assume circa il valore di massa. Non passa corrente nel canale di elettroni.
Questo circuito ha la caratteristica di dissipare potenza trascurabile nelle condizioni stazionarie,
mentre nei transitor viene dissipata potenza ma di piccola entità.
Questo circuito, in campo digitale, viene impiegato come invertitore, quindi come struttura di base
per costruire I blocchi logici fondamentali come le porte AND , NAND etc.