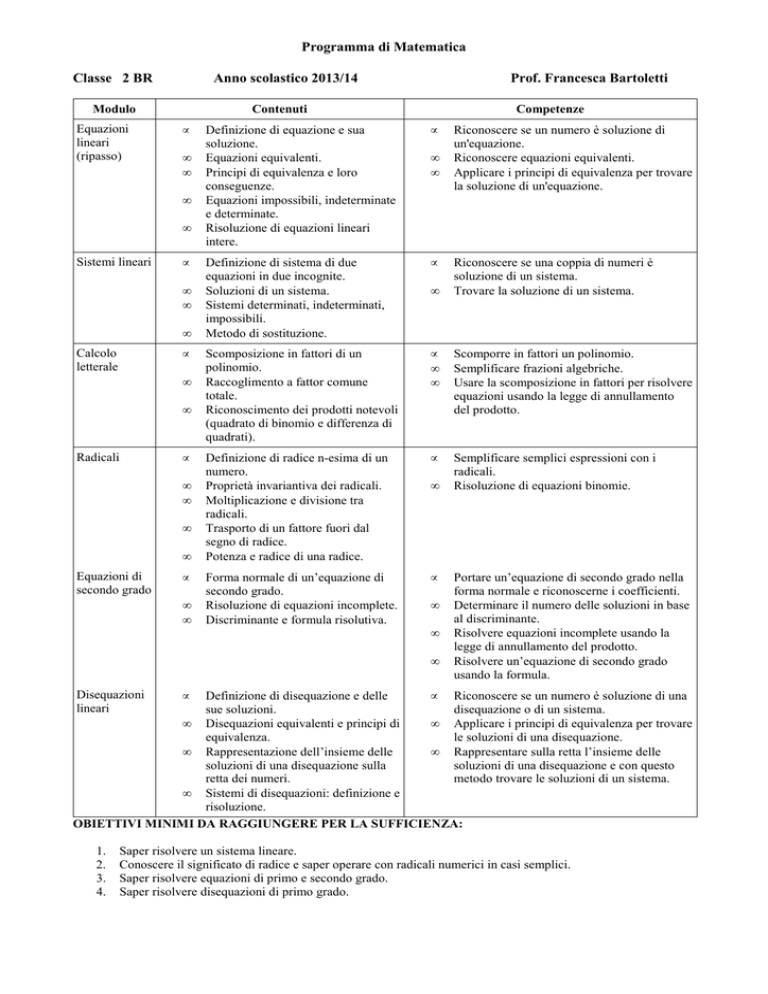
Programma di Matematica
Classe 2 BR
Anno scolastico 2013/14
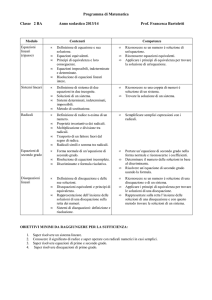
Modulo
Equazioni
lineari
(ripasso)
Contenuti
•
•
•
•
•
Sistemi lineari
•
•
•
•
•
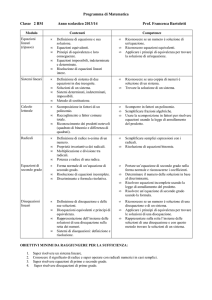
Calcolo
letterale
•
•
Radicali
•
•
•
•
•
Equazioni di
secondo grado
Prof. Francesca Bartoletti
•
•
•
Competenze
Definizione di equazione e sua
soluzione.
Equazioni equivalenti.
Principi di equivalenza e loro
conseguenze.
Equazioni impossibili, indeterminate
e determinate.
Risoluzione di equazioni lineari
intere.
•
Definizione di sistema di due
equazioni in due incognite.
Soluzioni di un sistema.
Sistemi determinati, indeterminati,
impossibili.
Metodo di sostituzione.
•
Scomposizione in fattori di un
polinomio.
Raccoglimento a fattor comune
totale.
Riconoscimento dei prodotti notevoli
(quadrato di binomio e differenza di
quadrati).
•
•
•
Scomporre in fattori un polinomio.
Semplificare frazioni algebriche.
Usare la scomposizione in fattori per risolvere
equazioni usando la legge di annullamento
del prodotto.
Definizione di radice n-esima di un
numero.
Proprietà invariantiva dei radicali.
Moltiplicazione e divisione tra
radicali.
Trasporto di un fattore fuori dal
segno di radice.
Potenza e radice di una radice.
•
Semplificare semplici espressioni con i
radicali.
Risoluzione di equazioni binomie.
Forma normale di un’equazione di
secondo grado.
Risoluzione di equazioni incomplete.
Discriminante e formula risolutiva.
•
•
•
•
•
•
•
•
Riconoscere se un numero è soluzione di
un'equazione.
Riconoscere equazioni equivalenti.
Applicare i principi di equivalenza per trovare
la soluzione di un'equazione.
Riconoscere se una coppia di numeri è
soluzione di un sistema.
Trovare la soluzione di un sistema.
Portare un’equazione di secondo grado nella
forma normale e riconoscerne i coefficienti.
Determinare il numero delle soluzioni in base
al discriminante.
Risolvere equazioni incomplete usando la
legge di annullamento del prodotto.
Risolvere un’equazione di secondo grado
usando la formula.
Definizione di disequazione e delle
• Riconoscere se un numero è soluzione di una
sue soluzioni.
disequazione o di un sistema.
• Disequazioni equivalenti e principi di
• Applicare i principi di equivalenza per trovare
equivalenza.
le soluzioni di una disequazione.
• Rappresentazione dell’insieme delle
• Rappresentare sulla retta l’insieme delle
soluzioni di una disequazione sulla
soluzioni di una disequazione e con questo
retta dei numeri.
metodo trovare le soluzioni di un sistema.
• Sistemi di disequazioni: definizione e
risoluzione.
OBIETTIVI MINIMI DA RAGGIUNGERE PER LA SUFFICIENZA:
Disequazioni
lineari
1.
2.
3.
4.
•
Saper risolvere un sistema lineare.
Conoscere il significato di radice e saper operare con radicali numerici in casi semplici.
Saper risolvere equazioni di primo e secondo grado.
Saper risolvere disequazioni di primo grado.