Variabili aleatorie

Variabili aleatorie
X (ω )
ℜ
ω
x
S
a.a. 2013-2014
1
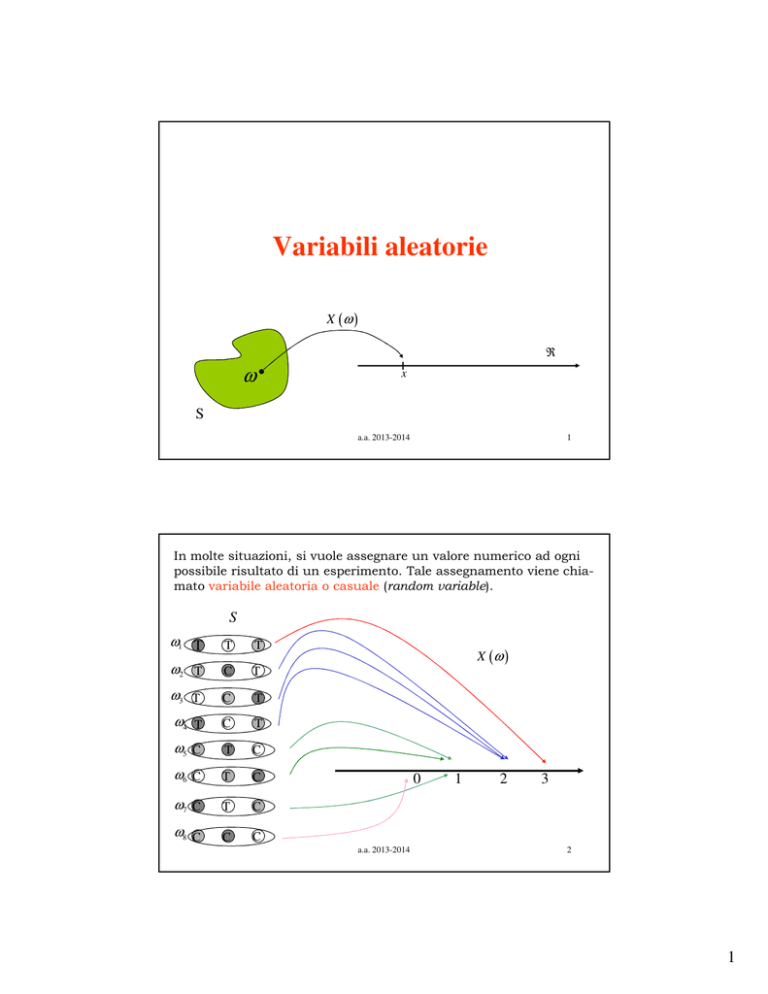
In molte situazioni, si vuole assegnare un valore numerico ad ogni
possibile risultato di un esperimento. Tale assegnamento viene chiamato variabile aleatoria o casuale (random variable).
S
ω1 T
T
T
ω2 T
C
T
ω3 T
C
T
ω4 T
C
T
ω5 C
T
C
ω6 C
T
C
ω7 C
T
C
ω8 C
C
C
X (ω )
0
a.a. 2013-2014
1
2
3
2
1
In molte situazioni, si vuole assegnare un valore numerico ad ogni
possibile risultato di un esperimento. Tale assegnamento viene chiamato variabile aleatoria o casuale (random variable).
X (ω )
S
ω1
T
T
T
ω2
T
C
T
ω3 T
C
T
ω4 T
C
T
ω5 C
T
C
ω6 C
T
C
ω7 C
T
C
ω8 C
C
C
1
P ({ω1} ) =
8
1
P ({ω2 } ) =
8
1
P ({ω3 } ) =
8
1
P ({ω4 } ) =
8
1
P ({ω5 } ) =
8
1
P ({ω6 } ) =
8
1
P ({ω7 } ) =
8
1
P ({ω8 } ) =
8
a.a. 2013-2014
3
2
2
P ( X = 2) = ?
2
1
1
1
0
3
P ( X = 2) = ?
( X = 2) = {
T
P ( X = 2) = P{
=
x
P(X=x)
C
T
,
T
T
C
T
,
C
T
,
T
C
T
T
C
,
T
T
C
}
T
}
3
8
0
1
2
3
1/8
3/8
3/8
1/8
Massa di probabilità
Distribuzione di probabilità
4
a.a. 2013-2014
2
La variabile aleatoria che abbiamo così caratterizzato prende il
nome di variabile aleatoria binomiale.
IPOTESI
1. Prove di Bernoulli (dicotomiche)
2. Probabilità di successo costante nelle prove.
p
3. Prove indipendenti.
n
4. Numero delle prove fissato.
X ∼ B ( n, p )
a.a. 2013-2014
5
Funzione di ripartizione
(CDF=cumulative distribution function)
F ( x) = P ( X ≤ x ) per ogni x ∈ℜ
Nel caso dell’esempio effettuato:
x<0
 0
1/ 8 x ∈ [0,1)

F ( x) = 1/ 2 x ∈ [1, 2)
7 / 8 x ∈ [2,3)

x≥3
 1
a ) lim F ( x) = 1 e lim F ( x) = 0
x →∞
x →−∞
b) x1 ≤ x2 ⇒ F ( x1 ) ≤ F ( x2 )
In R
a.a. 2013-2014
6
3
Istruzione di assegnazione
Seq : crea una sequenza di valori tra 0
e 3 con passo 1
tt stampa il vettore creato a video
Per creare una funzione a gradini le istruzioni sono:
Per aprire la finestra grafica…
a.a. 2013-2014
7
Per stampare in PDF questo grafico
NB: Nella prova scritta è necessario
includere i grafici in formato pdf.
a.a. 2013-2014
8
4
La v.a. binomiale X restituisce il numero di successi ottenuti in n prove
bernoulliane (indipendenti e dicotomiche)
Per creare un grafico della massa di probabilità….
…a punti (trattandosi di serie discreta)
a.a. 2013-2014
9
E’ possibile aprire uno script-file
dove memorizzare la successione
di istruzioni che produce il grafico
Per eseguire un file, salvare il codice
nella directory corrente…
a.a. 2013-2014
10
5
Altri grafici: Istogrammi
> tt<-seq(0,10,by=1)
> y<-dbinom(tt,10,0.5)
>plot(tt,y,type='h',col='red',lwd=10,
main='Funz. densità',
xlab='Successi',ylab=‘f(x)')
>
Usare l’help per conoscere i possibili parametri di input:
Help in formato http
a.a. 2013-2014
11
Esempio help on line
Per ripulire la console…
a.a. 2013-2014
12
6
Esercizio: Si è affermato che per il 60% di tutti gli impianti a energia
solare la bolletta si è ridotta di almeno di un terzo.
Qual è la probabilità che la bolletta si sia ridotta di almeno un terzo per
(a) quattro impianti su cinque;
(b) almeno quattro impianti su cinque.
n = 5, p = 0.60
(a ) P( X = 4) = ?
(b) P( X ≥ 4) = ?
⊳ ( X ≥ 4) = ( X = 4) + ( X = 5)
⊳ P( X ≥ 4) = P( X = 4) + P( X = 5)
⊳ P ( X ≥ 4) = 1 − P ( X < 4)
⊳ P ( X ≥ 4) = 1 − P ( X ≤ 3) = 1 − F (3)
a.a. 2013-2014
13
Per calcolare la funzione di ripartizione
Per effettuare il grafico
> tt<-seq(0,5,by=1)
> y<-pbinom(tt,5,0.6)
plot(tt,y,type='s',col='red',lwd=6,
main='Funz. distribuzione binomiale',
xlab='Successi',ylab='F(x)')
>
Per rispondere al quesito
a.a. 2013-2014
14
7
I quantili
Il quantile di ordine α è un valore xα che divide la massa di probabilità in due
parti: una proporzionale a α e l'altra proporzionale a 1 − α .
F ( xα ) ≥ α , α ∈ (0,1)
In R la sintassi è
Supponiamo di voler calcolare
x 0 .6 7
a.a. 2013-2014
15
In termini di massa di probabilità
Il grafico nasce dalla sovrapposizione
di due grafici.
A differenza del MATLAB questa
operazione in R è più complicata
> tt<-seq(0,5,by=1)
> y<-dbinom(tt,5,0.6)
> plot(tt[1:5],y[1:5],type='h',col='red',
lwd=6,main='Quantili',xlim=range(0,5),
ylim=range(0,0.4),xlab=' ',ylab=' ')
> par(new=TRUE)
> plot(tt[6],y[6],type='h',col='green',
lwd=4,xlim=range(0,5),ylim=range(0,0.4),
xlab='Successi',ylab='f(x)')
>
a.a. 2013-2014
16
8
(mean/expectation)
E[ X ] = 0 × P ( X = 0) + 1× P ( X = 1) + 2 × P ( X = 2) + 3 × P ( X = 3) + 4 × P ( X = 4) + 5 × P ( X = 5)
(variance)
Var[ X ] = (0 − 3) 2 × P ( X = 0) + (1 − 3) 2 × P ( X = 1) + ⋯ + (5 − 3) 2 × P ( X = 5)
(standard deviation)
a.a. 2013-2014
17
Sul significato di media
0
1
2
3
4
5
Sul significato di varianza
0
1
2
3
a.a. 2013-2014
4
5
18
9
• Grafici asimmetrici e valori di p
19
a.a. 2013-2014
X = X1 + X 2 + ⋯ + X n
E[ X ] = E[ X1 ] + E[ X 2 ] + ⋯ + E[ X n ]
Var[ X ] = Var[ X1 ] + ⋯ + Var[ X n ]
Variabile aleatoria di Bernoulli
E[ X ] = p
Var[ X ] = (0 − p ) 2 (1 − p ) + (1 − p ) 2 p
= p(1 − p )
a.a. 2013-2014
20
10
Spazio campione 3 Si consideri l’esperimento casuale che consiste
nel lanciare un dado e nell’osservare le facce
che si presentano.
X
1
2
3
4
5
6
a.a. 2013-2014
21
a.a. 2013-2014
22
per n = 6 è
> x<-seq(1,6,by=1)
> y<-dunif(x,min=0,max=6)
>y
[1] 0.16 0.16 0.16 0.16 0.16 0.16
>plot(x,y,type='h',col='red',lwd=4,
main='Massa di prob. uniforme',
xlab='Facce del dado',ylab='f(x)')
>
11
• Distribuzione uniforme discreta (funzione ripartizione)
> x<-seq(1,6,by=1)
> y<-punif(x,min=0,max=6)
> plot(x,y,type='s',col='red',lwd=4,main='Funz. ripartizione uniforme',
xlab='Facce del dado',ylab='F(x)')
>
a.a. 2013-2014
23
Simulazione del lancio del dado
• Viene generato un numero u
a caso tra 0 e 1.
• Si assume uscita la faccia
del dado che corrisponde
al valore x assunto dalla
v.a. tale che
F ( x) ≥ u
Questo schema di generazione è valido per tutte le leggi di distribuzione
> u<-runif(1,0,1)
>u
[1] 0.9199806
>
Poiché 0.91>5/6, allora la faccia generata è 6
>x3<-sample(1:10,5,replace=T)
a.a. 2013-2014
24
12
T
T
C
ω1 = T
ω2 = CT
ω3 = CCT
ω4 = CCCT
T
T
C
C
T
C
T
C
a.a. 2013-2014
25
C
P ( X ≥ n + m | X ≥ n) = P( X > m)
E[X ] =
1
p
Var [ X ] =
a.a. 2013-2014
1− p
p2
26
13
Gioco del lotto
Sia E l’evento ‘estrazione (prima) del numero 1 sulla ruota di Roma’
P( E ) =
1
17
, P( E C ) =
18
18
Il numero di settimane di ritardo dell’evento E è una v.a. con legge
n
geometrica:
 17 
P ( X > n) =  
 18 
P ( X = a + r | X > a) = P ( X = r )
L’attesa residua ha la stessa
distribuzione di probabilità
dell’attesa dall’inizio
a.a. 2013-2014
27
• Distribuzione geometrica
> x<-seq(1,100,by=1)
> y<-dgeom(x,0.5)
> plot(x,y,type='h',col='red',lwd=4,main='Massa di prob. geometrica',
xlab='Numero di lanci per avere un successo',ylab='f(x)')
>
a.a. 2013-2014
28
14
Confronto tra funz. ripartizione
>plot(x,y,type='s',col='red',
lwd=4, main='Funz. Ripartizio
ne geometrica', ylim=range(0,1),xlim=range(0,100),
xlab=‘ ',ylab=‘ ')
> y<-pgeom(x,0.1)
> par(new=TRUE)
>plot(x,y,type='s',col='green',
lwd=4, ylim=range(0,1),
xlim=range(0,100),
xlab='Num. lanci ',ylab='F(x)')
>
Il raggiungimento della massa 1 avviene
più velocemente per p=0.5.
> legend(80,0.5,c("p=0,5","p=0,1"),lty=c(1,1),lwd=c(2.5,2.5),col=c(“red",“green"))
Esercizio: Un esperto tiratore colpisce un bersaglio il 95% delle volte. Qual è
la probabilità che il tiratore manchi il bersaglio per la prima volta al quindicesimo colpo?
a.a. 2013-2014
E[X ] = λ
29
Var [ X ] = λ
15
> x<-seq(0,20,by=1)
> y<-dpois(x,2)
> plot(x,y,type='h',col='red',lwd=4,main=‘Massa prob. lam=2',
xlab=‘Num. difetti', ylab='f(x)')
>
a.a. 2013-2014
31
> x<-seq(0,20,by=1)
> y<-dpois(x,5)
> plot(x,y,type='h',col='red',lwd=4,main=‘Massa prob. lam=5',
xlab=‘Num. difetti', ylab='f(x)')
>
a.a. 2013-2014
32
16
A confronto, massa di probabilità di v.a. di Poisson e di v.a.
binomiale
Le due distribuzioni appaiono molto simili.
Se proviamo ad aumentare i parametri…
a.a. 2013-2014
33
> x<-seq(0,100,by=1)
> y<-dpois(x,50)
>plot(x,y,type='h',col='red',lwd=4,
main=‘Massa prob. lam=50',
xlab=‘Num. difetti', ylab='f(x)',ylim=range(0,0.06))
> x<-seq(0,100,by=1)
> y<-dbinom(x,500,1/10)
>plot(x,y,type='h',col='red',lwd=4,
main=Massa prob. (500,1/10)',
xlab=‘Num. difetti', ylab='f(x)',ylim=range(0,0.06))
a.a. 2013-2014
34
17
Al crescere di n e p, la massa di probabilità di una v.a. binomiale
tende a ....
?
Questo risultato prende il nome di teorema centrale del limite.
a.a. 2013-2014
35
18
> x<-seq(0,10,by=1)
> y<-dhyper(x,20,80,10)
> plot(x,y,type='h',col='red',lwd=4,main=‘Massa. iperg. (20,80,10)',
xlab=‘Num.suc.', ylab='f(x)')
>
10 estrazioni senza reimissione
da un’urna con 20 palline bianche
e 80 palline nere
a.a. 2013-2014
37
19
Binomiale e ipergeometrica
a confronto
In statistica:
- Campionamento da popolazione
finita con o senza reimmissione
- Campionamento da popolazione
infinita
a.a. 2013-2014
39
Distribuzione di Pascal
Definizione
In una successione di prove di Bernoulli, con probabilità di
successo p, sia Wr la v.a. che conta il numero di prove necessarie per avere l'r -esimo successo. Tale v.a. ha distribuzione
di Pascal di parametri p e r e massa di probabilità data da:
 x −1  r
x−r
f ( x) = 
 p (1 − p ) ,
x−r
x = r , r + 1,...
Se poniamo y =x − r ⇒ x = y + r
Poni Y = Wr − r ⇒ P(Y = k ) = P(Wr = r + k )
Wr descrive il numero di prove (non di insuccessi) prima di avere
l'r -esimo successo
a.a. 2013-2014
40
20
Distribuzione binomiale negativa
Definizione
In una successione di prove di Bernoulli, con probabilità di
successo p, sia Wk la v.a. che conta il numero di prove necessarie per avere il k -esimo successo. La v.a. Wk - k ha distribuzione binomiale negativa di parametri p e k e massa di
probabilità data da:
 x + k − 1 k
x
f ( x) = 
 p (1 − p ) ,
 x

x = 0,1,...
> x<-seq(0,15,by=1)
> y<-dnbinom(x,3,0.5)
> plot(x,y,type='h',col='red',lwd=4,main='Massa prob. r=3 p=0.5', xlab='Num.prove',
ylab='f(x)',ylim=range(0,0.3),xlim=range(0,15))
> x<-seq(0,15,by=1)
> y<-dnbinom(x,5,0.5)
> plot(x,y,type='h',col='red',lwd=4,main='Massa prob. r=5 p=0.5', xlab='Num.prove',
ylab='f(x)',ylim=range(0,0.3), xlim=range(0,15))
a.a. 2013-2014
42
21
> x<-seq(0,15,by=1)
> y<-dnbinom(x,3,0.5)
> plot(x,y,type='h',col='red',lwd=4,main='Massa prob. r=3 p=0.5', xlab='Num.prove',
ylab='f(x)',ylim=range(0,0.3),xlim=range(0,15))
> x<-seq(0,15,by=1)
> y<-dnbinom(x,3,0.3)
> plot(x,y,type='h',col='red',lwd=4,main='Massa prob. r=3 p=0.3', xlab='Num.prove',
ylab='f(x)',ylim=range(0,0.3), xlim=range(0,15))
a.a. 2013-2014
43
La v.a. geometrica è un caso particolare della v.a. binomiale negativa.
y<-dnbinom(1:15,1,0.5)
y<-dgeom(1:15,0.5)
a.a. 2013-2014
44
22
Domanda : Sia Tk = Wk − Wk −1 la v.a. che restituisce
il numero di prove tra il (k -1)-esimo successo e il
k -esimo successo. Qual è la distribuzione di Tk ?
Distribuzione geometrica
Media e varianza della distribuzione di Pascal:
E[X ] =
r
p
Var [ X ] = r
1− p
p2
Per avere la distribuzione di Pascal basta shiftare la distribuzione
binomiale negativa in avanti
a.a. 2013-2014
46
23
1. Due squadre di basket si sfidano a una serie di incontri. Il primo
team che vince 4 partite è dichiarato vincitore della sfida. Supponiamo che una delle due squadre sia più forte dell’altra e che vinca ogni
singola partita con probabilità 0.6, indipendentemente dagli altri incontri. Si trovi la probabilità che il team più forte vinca la sfida in
esattamente i incontri, con i=5,6,7.
2. Si lancia 4 volte una moneta equilibrata. Sia X il numero totale
di teste ottenute. Calcolare la distribuzione di probabilità di X-2.
3. Un certo tipo di missile ha probabilità di fallimento 0.02.
Calcolare la distribuzione della variabile aleatoria che conta il numero
di lanci prima di avere il primo fallimento.
Discreto continuo
Uniforme
Uniforme
Uniforme
Uniforme
discreta,
discreta,
discreta,
discreta,
n=101
n=21
n=11
n=6
n=501
n=51
0.18
0.18
0.16
0.16
0.14
0.14
?
0.12
0.12
Uniforme
0.1
0.1
0.08
0.08
0.06
0.06
0.04
0.04
0.02
0.02
00
00
11
22
33
44
55
66
77
Per passare dal modello discreto al modello continuo non basta
solo “infittire” i valori del range perché le probabilità vanno a
zero!!
24
0.1818=(1/11)/0.5
0.1961=(1/51)/0.1
0.1996=(1/501)/0.01
0.2=(1/5001)/0.001
F ( xi ) = ∑ f ( x) ⇒ F ( xi ) =
x ≤ xi
xi
∫
f ( x)dx
−∞
X variabile aleatoria continua
25
26
a=0
b=1
a=0
b=1
27
Le istruzioni per creare il grafico precedente
> x<-seq(-0.5,0,by=0.1)
> y<-x*0
> plot(x,y,type='l',col='red',lwd=4,main='Distrib. uniforme',ylab='F(x)',
xlim=range(-0.5,1.5),ylim=range(-0.2,1.2))
> par(new=TRUE)
> x<-seq(0,1,by=0.1)
> y<-punif(x,min=0,max=1)
> plot(x,y,type='l',col='red',lwd=4,ylab=' ',xlim=range(-0.5,1.5),
ylim=range(-0.2,1.2))
> par(new=TRUE)
> x<-seq(1,1.5,by=0.1)
> y<-rep(1,6)
plot(x,y,type='l',col='red',lwd=4,ylab=' ',xlim=range(-0.5,1.5),
ylim=range(-0.2,1.2))
>
a.a. 2013-2014
55
Al crescere di n e p, la massa di probabilità di una v.a. binomiale
tende a ....
?
Questo risultato prende il nome di teorema centrale del limite.
a.a. 2013-2014
56
28
Grafici della densità gaussiana al
variare della media -3, 0, 3 e parità
di deviazione standard 1.
Variare la media equivale a shiftare
la curva lungo l’asse delle ascisse.
Le istruzioni per creare il grafico precedente
> x<-seq(-8,8,0.1)
> y<-dnorm(x,mean=0,sd=1)
> plot(x,y,type='l',col='red',lwd=4,main='Guassiana media=-3,0,3',
ylab='f(x)',ylim=range(0,0.4),xlim=range(-8,8))
> par(new=TRUE)
> y1<-dnorm(x,mean=-3,sd=1)
> plot(x,y1,type='l',col='green',lwd=4,ylab='',ylim=range(0,0.4),
xlim=range(-8,8))
> par(new=TRUE)
> y2<-dnorm(x,mean=3,sd=1)
> plot(x,y2,type='l',col='blue',lwd=4,ylab='',ylim=range(0,0.4),
xlim=range(-8,8))
> legend(3,0.35,c("m=-3","m=0","m=3"),lty=c(1,1,1),lwd=c(2.5,2.5,2.5),
col=c('green','red','blue'))
>
a.a. 2013-2014
58
29
Grafici della densità gaussiana al
variare della deviazione standard
0.4,1, 3 e parità di media 0.
Variare la deviazione standard equivale a variare la distribuzione della
massa di probabilità lungo l’asse
delle ascisse.
Esercizio: Rifare i due grafici in R usando l’esempio nella pagina
precedente
Cosa accade alle funzioni di ripartizione?
a.a. 2013-2014
60
30
I quantili
I quantili di una gaussiana sono molto utili in statistica.
> qnorm(0.95,mean=0,sd=1)
[1] 1.644854
> qnorm(0.65,mean=0,sd=1)
[1] 0.3853205
Variabile aleatoria standardizzata
Prop: Sia X una v.a. gaussiana N ( µ , σ 2 ). La v.a. Z =
X −µ
σ
è
gaussiana N (0,1)
Infatti trasformate lineari di v.a. gaussiane sono ancora gaussiane.
Inoltre
X −µ 1
E [Z ] = E 
= E[X − µ] = 0
 σ  σ
1
X −µ 1
Var [ Z ] = Var 
= 2 Var [ X − µ ] = 2 Var [ X ] = 1

σ
 σ  σ
a.a. 2013-2014
62
31
ESERCIZI
1. Determinare la probabilità che una variabile aleatoria normale
standard assuma un valore compreso tra 0.87 e 1.28 e tra -0.34 e 0.62,
maggiore di 0.85
2. Determinare z0.01 , ossia quel valore tale che
P ( Z > z 0.01 ) = 0.01
3. In un processo fotografico il tempo di sviluppo delle stampe può
essere considerato una variabile casuale avente distribuzione normale
con una media di 16.28 sec e una deviazione standard di 0.12 sec.
Determinare la probabilità che assuma un valore compreso tra 16.00
e 16.50 secondi; almeno 16.20 secondi; al massimo 16.35
Il comando in R per disegnare la
densità esponenziale è dexp(…)
La v.a. esponenziale è spesso impiegata
nello studio dell’affidabilità dei sistemi,
come modello di tempo fino alla sua
rottura
32
ESERCIZI
1. Una popolazione di bambini di una scuola romana è stata sottoposta
a un test con una batteria di domande. L’andamento della distribuzione
dei punteggi conseguiti è risultato di tipo normale, con varianza pari a
10. La percentuale di bambini che ha riportato un punteggio inferiore
a 112 è risultata pari al 91,92%. Calcolare la media della distribuzione.
2. Il tempo in ore necessario alla riparazione di un macchinario è una
variabile aleatoria esponenziale di parametro 1. Determinare la probabilità che la riparazione superi le 2 ore di tempo.
3. Arrivi alla fermata dell’autobus alle 10 e sei certo che l’autobus passerà in un momento qualsiasi uniformente distribuito tra le 10 e le 10.30.
Qual è la probabilità che tu debba aspettare più di 10 minuti? Se alle
10.15 l’autobus non è ancora arrivato, qual è la probabilità che tu debba
aspettare almeno altri 10 minuti?
33