Soluzioni di Adriana Lanza
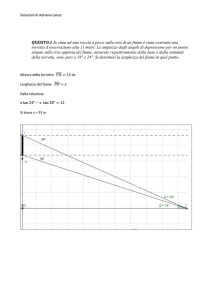
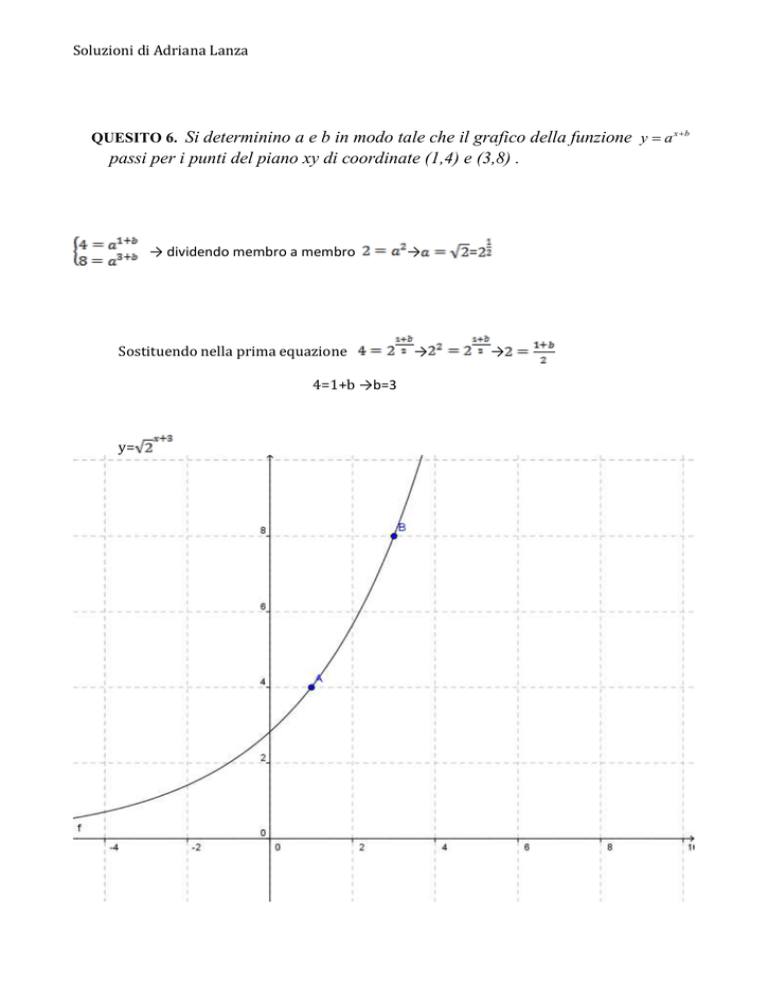
QUESITO 6. Si determinino a e b in modo tale che il grafico della funzione y a x b
passi per i punti del piano xy di coordinate (1,4) e (3,8) .
→ dividendo membro a membro
Sostituendo nella prima equazione
4=1+b →b=3
y=
→
→
=
→
Soluzioni di Adriana Lanza
QUESITO7. Un tetraedro ed un ottaedro regolari hanno gli
spigoli della stessa lunghezza l. Si dimostri che il volume
dell’ottaedro è il quadruplo di quello del tetraedro.
Prima dimostrazione :Calcolo dei due volumi, che
indicheremo con V1 e V2 rispettivamente, in funzione dello
spigolo l
tetraedro
=
l
Volume tetraesdro =
Ottaedro
Il volume è il doppio di quello di una piramide avente
per base un quadrato di lato l e altezza pari a
Volume ottaedro =
=
V2 = 4 V1
=
Soluzioni di Adriana Lanza
Seconda dimostrazione (geometrica)
Le figure seguenti mostrano che:
a) L’ottaedro di spigolo l può essere inscritto in un tetraedro di spigolo 2l, quindi di
volume pari a 8 V1
b) Il tetraedro di spigolo 2l può essere decomposto in 5 parti, di cui una è l’ottaedro, le
altre quattro consistono in tetraedri di spigolo l, quindi di volume pari a V1
Pertanto
8V1= V2+4 V1
Da cui
V2= 4 V1
Soluzioni di Adriana Lanza
QUESITO8. Si trovi l’equazione della retta tangente alla curva di equazioni parametriche
x = 2t e y
2
nel suo punto di coordinate (2,1) .
t 1
2
Primo metodo
Dalle equazioni parametriche si passa facilmente all’ equazione cartesiana della curva,
eliminando il parametro t.
La curva passa effettivamente per il punto (2,1) che corrisponde al valore t=1 del parametro.
Nel suddetto punto la retta tangente ha coefficiente angolare m= y’(2)
→
Equazione della retta tangente x+2y-4=0
Secondo metodo
Le funzioni x(t) e y(t) , che rappresentano le coordinate di un generico punto della curva ,
sono continue e derivabili e il coefficiente angolare m della retta tangente nel punto (2;1) è
uguale al rapporto
Poiché x’(t) = 2
metodo
si trova m=
, ovvero lo stesso risultato del primo
Soluzioni di Adriana Lanza
QUESITO9. Si dimostri che se una funzione f(x) è derivabile nel punto x0 , ivi è anche
continua; si porti un esempio di funzione continua in un punto e ivi non derivabile.
Ipotesi: f(x) è derivabile in xo → finito
lim f ( x) f ( x0 )
f ' ( x0 )
x x0
x x0
Tesi : f(x) è continua in xo.
f(x) è continua in xo se
lim
f ( x) f ( x0 ) ovvero
x x0
Dall’identità
h si deduce
=
quindi
c.v.d.
Il risultato precedente è conseguenza diretta del fatto che, al tendere di h a 0, il limite del
rapporto incrementale esiste ed è finito. Se il suddetto limite non esiste o è infinito, nulla si
può dire del limite
.
La continuità è pertanto condizione necessaria per la derivabilità, ma non è condizione
sufficiente, poiché esistono funzioni continue in un punto ma ivi non derivabili
Esempio 1 : punto angoloso
Sia f(x) un funzione continua e
derivabile in x0 e sia
f(x0)=0
f(x)>0 in un intorno destro di x0
f(x) <0 in un intorno sinistro di x0
La funzione
non è derivabile in x0 in quanto
=- f’( )
= f’( )
Soluzioni di Adriana Lanza
La derivata prima ammette in xo una discontinuità di prima specie
Esempio 2. Cuspide
La funzione
è continua in O(0,0) ma non è ivi derivabile
Se proviamo a calcolare il limite del rapporto incrementale, per h tendente a 0,
troviamo
=
=
La derivata prima
ammette in O una discontinuità di seconda specie
Soluzioni di Adriana Lanza
Esempio 3 Flesso a tangente verticale
La funzione
è continua in O(0,0) ma non è ivi derivabile
Se proviamo a calcolare il limite del rapporto incrementale, per h tendente a 0,
troviamo
=
=
La derivata
ammette in O un discontinuità di seconda specie
La derivata seconda
è positiva per x<0 e negativa per x>0
Soluzioni di Adriana Lanza
Esempio 4 Punto isolato
Il valore x=-1 appartiene al dominio ed è un punto isolato.
Per definizione la funzione è ivi continua, ma non è possibile definire la derivata
Soluzioni di Adriana Lanza
QUESITO10. Si dimostri che la differenza dei quadrati di due lati di un triangolo è uguale alla
differenza dei quadrati delle rispettive proiezioni dei lati stessi sul terzo lato del triangolo.
Con riferimento alla figura :
Si deve dimostrare che
Osserviamo che
c.v.d.