quesiti 6-10

SOLUZIONI di Adriana Lanza
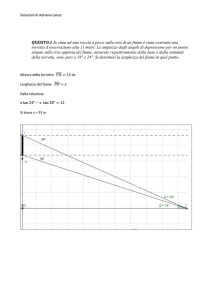
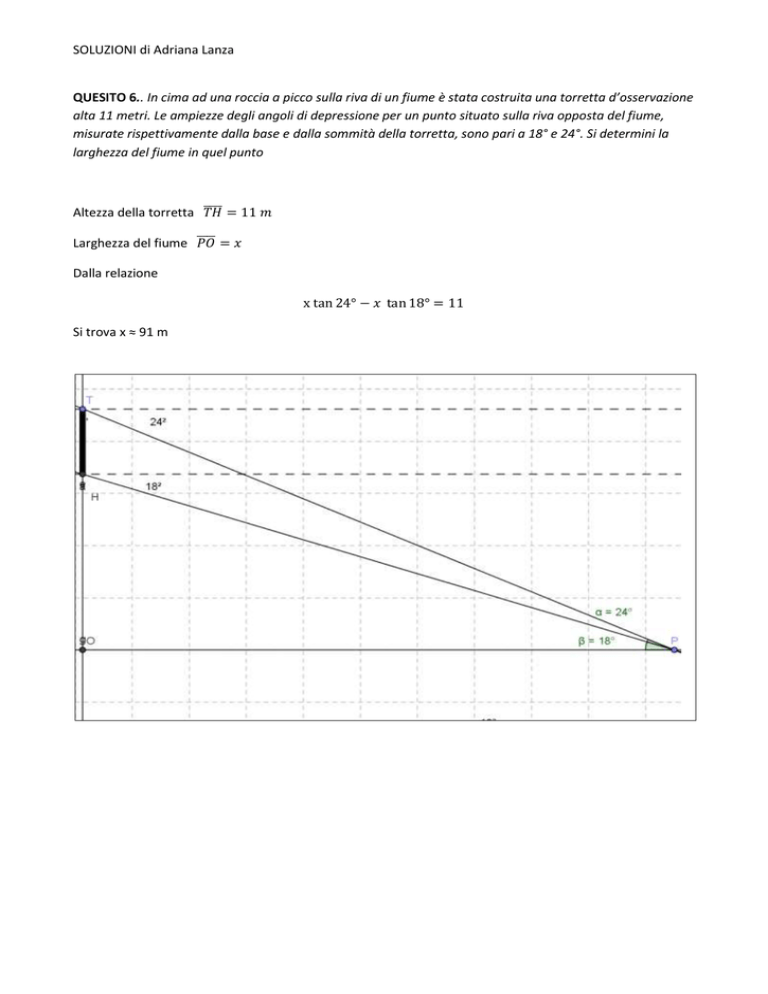
QUESITO 6.. In cima ad una roccia a picco sulla riva di un fiume è stata costruita una torretta d’osservazione
alta 11 metri. Le ampiezze degli angoli di depressione per un punto situato sulla riva opposta del fiume,
misurate rispettivamente dalla base e dalla sommità della torretta, sono pari a 18° e 24°. Si determini la
larghezza del fiume in quel punto
̅̅̅̅ = 11 𝑚
Altezza della torretta 𝑇𝐻
Larghezza del fiume ̅̅̅̅
𝑃𝑂 = 𝑥
Dalla relazione
x tan 24° − 𝑥 tan 18° = 11
Si trova x ≈ 91 m
SOLUZIONI di Adriana Lanza
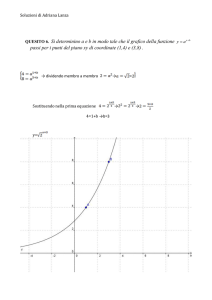
QUESITO 7. Considerata la funzione f ( x) 
33 x  a x
, dove a è una costante reale positiva, si determini
6 x  5x
tale costante, sapendo che lim f ( x)  2 .
x0
Il limite può essere calcolato applicando la regola di de l H𝑜̂pital
lim
27𝑥 ln 27−𝑎𝑥 ln 𝑎
𝑥→0 6𝑥 ln 6−5𝑥 ln 5
=
27
𝑎
6
ln
5
ln
Imponendo che il risultato sia uguale a 2
27
6
36
27
𝑎
5
25
𝑎
ln =2 ln = ln →
=
36
25
75
→a=
4
SOLUZIONI di Adriana Lanza
QUESITO 8. Su un piano orizzontale α si
pongono un cono circolare retto, il cui raggio di
base è r e l’altezza 2r, e una sfera di raggio r. A
quale distanza x dal piano α bisogna segare
questi due solidi con un piano orizzontale ß,
perché la somma delle aree delle sezioni così
ottenute sia massima
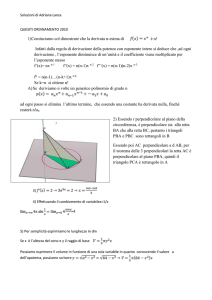
La figura seguente rappresenta le sezioni mediane dei due solidi
Le sezioni col piano ß sono , rispettivamente , un cerchio di raggio DH e un cerchio di raggio KF
Si ha inoltre
̅̅̅̅ = 𝐾𝐼
̅̅̅ = 𝑥
𝐻𝑂
̅̅̅̅ = 2𝑟 − 𝑥
𝐻𝑉
̅̅̅̅ = |𝑟 − 𝑥|
𝐶𝐾
0≤x≤2r
Dalla similitudine dei triangoli VDE e VAB si deduce
̅̅̅̅ = 2𝑟 − 𝑥 → 𝐷𝐻
̅̅̅̅ =
𝐷𝐸
2𝑟 − 𝑥
2
̅̅̅̅ = √𝑟 2 − (𝑟 − 𝑥)2 = √2𝑟𝑥 − 𝑥 2
Applicando il teorema di Pitagora al triangolo CFK si trova𝐾𝐹
La somma delle aree delle due sezioni è
2𝑟−𝑥 2
)
2
𝑆(𝑥) = 𝜋(
3
4
+ 𝜋(2rx-𝑥 2 ) = 𝜋(− 𝑥 2 + 𝑟𝑥 + 𝑟 2 )
S(x) rappresenta una parabola con la concavità rivolta verso il basso.
2
L’ascissa del vertice 𝑥𝑜 = 3 𝑟 è compresa nell’intervallo di variabilità dell’incognita e rappresenta il punto
di massimo per la funzione
SOLUZIONI di Adriana Lanza
QUESITO9. Si dimostri che per gli zeri x1 e x2 di una funzione f ( x)  ax 2  bx  c vale la relazione
f ' ( x1 )  f ' ( x2 )  0 e si dia una interpretazione geometrica della affermazione dimostrata.
Poiché f’(x) =2ax+b, si deve dimostrare che
2ax1+b+2ax2+b= 2a(x1+x2)+2b
Ricordando che , per le proprietà delle radici di un
‘equazione di secondo grado, x1+x2= -b/a si ottiene
-2b+2b=0 c.v.d.
Se non si vuol ricorrere alla suddetta formula, si può scrivere
f(x) nella forma
a(x-x1)(x-x2)→ f’(x) = a(x-x2)+a(x-x1)
da cui f’(x1) = a(x1-x2)
f’(x2) = a(x2-x1)→ f’(x1)+f’(x2)=0
Significato geometrico
f’(x1) e f’(x2) rappresentano i coefficienti angolari delle rispettive rette tangenti, nei punti in cui la parabola ,
associata ad f(x), incontra l’asse delle x.
Data la simmetria della curva rispetto all’asse della parabola(retta parallela all’asse y), le due tangenti
devono avere coefficienti angolari uguali e opposti
SOLUZIONI di Adriana Lanza
e x ( x  1)
QUESITO 10. Si calcoli il valore medio della funzione f ( x) 
, nell’intervallo 1 ≤ x ≤ 2 .
x2
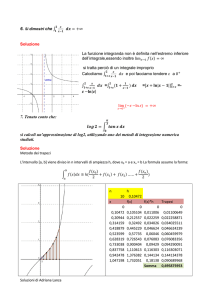
Valor medio
1
2 𝑒 𝑥 (𝑥−1)
𝑏
.𝑏−𝑎 ∫𝑎 𝑓(𝑥)𝑑𝑥 = ∫1
𝑥2
𝑒𝑥
𝑒2
dx =[ 𝑥 ]12 = 2 − 𝑒
Calcolo della funzione primitiva (Integrazione per parti )
∫
𝑒 𝑥 (𝑥−1)
𝑑𝑥
𝑥2
1
1
1
= − 𝑥 𝑒 𝑥 (𝑥 − 1) + ∫ 𝑥(x𝑒 𝑥 − 𝑒 𝑥 + 𝑒 𝑥 ) 𝑑𝑥=
− 𝑥 𝑒 𝑥 (𝑥 − 1) + ∫ 𝑒 𝑥 𝑑𝑥 = −𝑒 𝑥 +
𝑒𝑥
𝑥
+ 𝑒𝑥 =
𝑒𝑥
𝑥