B
Simmetrie e cristalli
In questa appendice richiameremo proprietà di enti geometrici molto elementari per mostrarne poi delle interessanti applicazioni in Cristallografia.
ria
Si considerino i punti A0 , A1 , A2 , . . . An con n ≥ 1; si dice spezzata
l’insieme dei segmenti congiungenti ciascun Ai con Ai+1 , i = 0, . . . , n − 1. I
punti A0 , A1 , A2 , . . . An si dicono vertici della spezzata e la spezzata si
dice chiusa se An = A0 .
A6
viso
A1
A3
A0
A2
A5
A4
za p
rov
Figura B.1. Esempio di spezzata aperta.
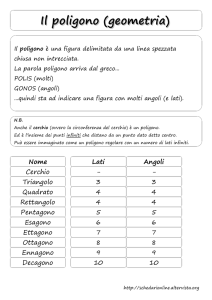
Si dice poligono ogni spezzata chiusa con almeno tre vertici. I segmenti della spezzata si dicono lati del poligono e gli estremi dei segmenti vertici del
poligono .
boz
Talvolta è utile pensare ai lati di un poligono che siano orientati concordemente come a n vettori aventi per somma zero.
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
p. 434
A3
A8
A9
A5
A4
A2
A6
A7
A0
A1
Figura B.2. Esempio di spezzata chiusa.
viso
ria
Se tutti i vertici di un poligono sono complanari il poligono si dice piano,
sghembo altrimenti. In base al Teorema di Jordan 1 un poligono piano divide
il piano che lo contiene in (almeno) due regioni di cui quelle limitate si dicono
interno del poligono. Un poligono si dice convesso se, presi comunque due
punti interni al poligono, il segmento che li unisce è interno al poligono; si
dice invece concavo se ciò non accade.
Figura B.3. Esempi di un poligono convesso (a sinistra) e di uno concavo (a destra)
Un poligono si dice equilatero se tutti i lati hanno la stessa lunghezza,
equiangolo se tutti gli angoli sono uguali.
za p
rov
Mentre ogni triangolo equiangolo è anche equilatero, nei quadrangoli i due
concetti sono indipendenti: infatti un rombo è equilatero ma non equiangolo
mentre un rettangolo è equiangolo ma non equilatero.
Un poligono si dice regolare se risulta sia equilatero che equiangolo.
Con l’ausilio della figura B.4 è facile vedere il seguente fatto
1
Una curva piana continua che non si autointerseca divide il piano in due regioni
di cui una limitata. Questo profondo risultato, apparentemente intuitivo, venne
dimostrato per la prima volta da Camille Jordan (1838 – 1922) nel suo Cours
d’Analyse.
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
p. 435
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
La somma degli angoli interni di un poligono convesso di n(≥ 3) lati è pari
a (n − 2) · π.
—◮ Dimostrazione. Preso infatti un punto interno O si considerino gli n triangoli individuati dal vertice O e dagli estremi di ciascun lato del poligono. Poiché
la somma degli angoli interni di un triangolo è l’angolo piatto2 e quindi misura
(in radianti) π, la somma degli angoli interni del poligono risulta dunque pari
alla somma degli angoli interni degli n triangoli (n · π) a cui va tolto l’angolo di
ampiezza 2π che costituisce la somma degli angoli di vertice O degli n triangoli.
◭—
ria
O
Figura B.4. La somma degli angoli interni di un poligono convesso con n lati è
pari alla somma degli angoli interni di n − 2 triangoli
viso
Pertanto ogni angolo interno di un poligono regolare misura (1 − 2/n) · π.
za p
rov
Ci chiediamo ora: è possibile ricoprire l’intero piano una sola volta usando
un solo tipo di poligono regolare con lato unitario, facendo combaciare lati e
vertici di poligoni adiacenti? Questo problema - noto anche come problema
della tassellatura del piano - ha chiaramente una soluzione dato che è possibile
pavimentare l’intero piano con quadrati di lato unitario, che non si accavallano
e che, se adiacenti, hanno in comune lati e vertici. La risposta generale è
pure sorprendentemente semplice. Poiché in un vertice possono convergere m
poligoni regolari di n lati, la condizione per la tassellatura del piano diventa
m(1 − 2/n)π = 2π
ossia
2
A questo risultato si arriva facilmente considerando, in un triangolo qualsiasi, la
retta per un vertice parallela al lato opposto. Essa individua, con gli altri due lati,
angoli congruenti agli angoli opposti al vertice, pertanto la somma degli angoli
interni di un triangolo è l’angolo piatto (vedere figura B.5).
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
p. 436
β
α
β
α
Figura B.5. La somma degli angoli interni di un triangolo è pari all’angolo piatto
m(n − 2) = 2n
ria
che possiamo equivalentemente scrivere nella forma
(m − 2)(n − 2) = 4.
Se ne deduce che le uniche soluzioni intere di questa equazione sono
viso
m=3 n=6
m=4 n=4
m=6 n=3
(B.1)
cioè oltre alla tassellatura del piano con quadrati è possibile la tassellatura
del piano con triangoli equilateri e con esagoni regolari.
La generalizzazione nello spazio IR3 dei poligoni piani è rappresentata dai
poliedri (in IRn , con n ≥ 4 dai politopi ).
za p
rov
Un poliedro è un insieme finito e connesso di poligoni piani tali che ogni lato
di ciascun poligono appartiene esattamente ad un altro poligono e con la
proprietà che i lati dei poligoni che concorrono a ciascun vertice rimangano
in un solo semispazio individuato da un piano passante per tale vertice. Gli
interni dei poligoni si dicono facce mentre i loro lati si dicono spigoli.
Esempi di poliedri sono le piramidi, i prismi e gli antiprismi.
Dalla definizione risulta che le facce non possono intersecarsi in un poliedro
e che non sono ammesse tra i poliedri situazioni tipo la “doppia piramide a
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
p. 437
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
(a)
(b)
(c)
(e)
(d)
ria
Figura B.6. Esempi di poliedri: piramidi [(a),(b)], prisma (c) e antiprismi [(d),(e)]
viso
clessidra”. Infine, come per i poligoni piani, appare chiaro che un poliedro
divide lo spazio in (almeno) due regioni, di cui quelle limitate costituiscono
l’interno. Un poliedro si dice convesso se nessun piano contenente le facce
interseca l’interno.
Un poliedro si dice regolare se tutte le facce sono poligoni regolari convessi
uguali tra loro e se ad ogni vertice concorrono lo stesso numero di spigoli.
za p
rov
Se, in un poliedro regolare le facce sono poligoni regolari con p lati e se a ogni
vertice concorrono q spigoli, il poliedro regolare si indica con {p, q}.
A differenza dei poligoni regolari convessi (che sono infiniti), di poliedri regolari convessi ce ne sono solo 5 come risulta da una banale generalizzazione
del ragionamento svolto per la determinazione delle tassellature regolari del
piano. Sia infatti dato un poliedro regolare e convesso {p, q}; se immaginiamo
di sviluppare su un piano passante per un vertice del poliedro le q facce che a
questo concorrono, dalla convessità segue che
q(1 − 2/p)π < 2π,
ossia, sviluppando,
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
1 1
1
+ > ;
p q
2
p. 438
(B.2)
pertanto le sole coppie intere {p, q} verificanti la (B.2) sono
p = 3, q = 3 p = 3, q = 4
p = 3, q = 5 p = 4, q = 3
p = 5, q = 3
che danno luogo, rispettivamente, ai poliedri detti tetraedro, ottaedro, icosaedro, cubo e dodecaedro. Complessivamente essi sono noti come solidi platonici3 .
Tetraedro
Cubo
Dodecaedro
ria
Ottaedro
Icosaedro
Cosı̀ chiamati perché descritti per la prima volta da Platone, il quale però attribuisce la scoperta di alcuni di essi ai Pitagorici. Questi, che del numero e delle
relazioni misurabili della geometria avevano fatto il fondamento della loro dottrina, ritenevano che i solidi in questione, per la loro regolarità, si interponevano tra
le sfere celesti (quindi implicitamente erano in grado di apprezzarne l’inscrivibilità in sfere) e queste, con il loro moto, nell’armonia dell’universo, producevano
suoni e musica, pure regolati da perfetti rapporti numerici. Infine va ricordato
che i primi quattro solidi platonici vennero descritti anche da Euclide e a questi
Platone, nel Timeo, associò i quattro elementi costitutivi dell’Universo, cioè fuoco (tetraedro), aria (ottaedro), acqua (icosaedro), e terra (cubo). Il quinto solido
platonico, ossia il dodecaedro, fu, secondo Platone, usato dal Creatore per decorare l’Universo; sempre nel medesimo dialogo, Platone afferma “non accorderemo
a nessuno che vi siano corpi visibili più belli di questi.” La bellezza e regolarità di
questi solidi vennero riscoperte durante il Rinascimento contemporaneamente ai
primi studi di prospettiva (si pensi al De quinque corporibus regolaribus di Piero
della Francesca o al De proportione di Luca Pacioli) per poi essere nuovamente
rivisitati in chiave esoterica dal neoplatonico Keplero.
za p
rov
3
viso
Figura B.7. I cinque solidi platonici
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
p. 439
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
ria
Vediamo infine, per completezza, il caso non convesso partendo dal piano. I
cosiddetti poligoni regolari a stella (noti già ai Pitagorici) sono poligoni non
convessi con lati ed angoli formati da lati consecutivi uguali fra loro, con
la possibilità per i lati di autointesecarsi. Il pentagono regolare stellato (o
stella a cinque punte) si ottiene ad esempio congiungendo in ordine alterno i
vertici di un pentagono regolare convesso. Analogamente si possono costruire
in IR3 dei poliedri regolari a stella che sono poliedri non convessi con facce
autointersecantesi fra loro. Si può dimostrare che anche i poliedri regolari a
stella (noti anche come poliedri di Keplero (1777 – 1859)4 sono in numero
finito; più precisamente tre dodecaedri stellati e un icosaedro stellato.
Matematico e astronomo, Keplero (J. Kepler, 1571 – 1630) detto Keplero) propose
un modello del sistema solare basato sui solidi platonici; a confermare l’atteggiamento pitagorico che ancora permeava la visione dell’Universo, ricordiamo che
nel libro L’armonia del mondo del 1619 Keplero descrisse le leggi musicali che regolano il moto dei pianeti in accordo con quanto asserito da Platone (e attribuito
ai pitagorici) e secondo le quali i rapporti armonici del moto dei pianeti corrispondono ai rapporti dell’ottava e della quinta (Timeo). Si noti che la famosa
terza legge di Keplero, poi usata da Newton per ricavare la legge di gravitazione
universale, ritrova il rapporto di quinta giacché asserisce che il quadrato del periodo di rivoluzione di un pianeta attorno al Sole è proporzionale al cubo della
sua distanza da esso (per la precisione la terza legge fa riferimento “al semiasse
maggiore” invece che “alla distanza” dato che l’orbita, in genere, risulta ellittica, col sole in uno dei fuochi). Il sistema solare, come complesso di sfere, veniva
sostanzialmente descritto attraverso i rapporti dei solidi platonici mentre ciascun
pianeta veniva interpretato come una corda di una lira a sette corde suonata da
Apollo: con il loro moto venivano prodotti i suoni che costituivano la musica delle
sfere. In particolare Keplero precisa che Mercurio canta da soprano, Marte da
tenore, Saturno e Giove da bassi e la Terra e Venere da alti.
za p
rov
4
viso
Figura B.8. Pentagono regolare stellato
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
Dodecaedro stellato
Dodecaedro stellato
di II specie
di III specie
Icosaedro stellato
ria
Dodecaedro stellato
p. 440
di VII specie
di IV specie
viso
Figura B.9. I poliedri di Keplero-Poinsot
Teorema di Eulero
za p
rov
Un poliedro si dice semplice se può essere deformato in modo continuo fino
a diventare una sfera, ovvero se il poliedro non presenta “buchi”. Più precisamente si potrebbe dire che presa comunque una curva chiusa sul poliedro,
essa può venir deformata in modo continuo fino ad un punto. Per i poliedri
semplici vale il seguente risultato.
Indichiamo con F il numero delle facce, con S il numero degli spigoli e con
V il numero dei vertici di un poliedro semplice. Allora 5
F − S + V = 2.
—◮ Dimostrazione. Si tolga una faccia del poliedro e, con movimenti continui,
si deformi il restante del poliedro fino a realizzare uno sviluppo piano.
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
p. 441
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
Naturalmente, con questo procedimento, il numero di vertici e il numero di spigoli del poliedro rimangono invariati; considerando l’esterno dello sviluppo piano
come la faccia rimossa, anche il numero delle facce del poliedro rimane inalterato.
Operiamo ora dei cambiamenti nello sviluppo piano del poliedro che non cambiano
la caratteristica di Eulero del poliedro, ossia la quantità F − S + V .
Su ogni faccia dello sviluppo piano con più di tre spigoli si aggiunga una diagonale (cioè
un segmento che unisce due vertici non consecutivi); ad ogni aggiunta di una diagonale
aumenterà di una unità sia S (si aggiunge uno spigolo) che F (si aggiunge una faccia).
Tuttavia rimane invariata la quantità F − S + V .
Si rimuovano quelle facce (ormai tutte triangolari) dello sviluppo piano che risultano avere
due spigoli sulla frontiera dello sviluppo stesso. In tal modo, ogni rimozione comporta la
diminuzione di una faccia, due spigoli e un vertice, rimanendo inalterata la quantità
F − S + V . Si ripeta questo procedimento fino a che tutte le facce dello sviluppo piano
rimanenti abbiano in comune con la frontiera o uno spigolo oppure lo sviluppo piano si
riduca ad un triangolo.
Si rimuovano quelle facce dello sviluppo piano aventi in comune con la frontiera uno
spigolo; ad ogni rimozione diminuiscono di una unità sia il numero delle facce che il
numero degli spigoli, pertanto resta invariata la quantità F − S + V .
ria
Alla fine, dopo aver ripetutamente operato i cambiamenti descritti nei punti a),
b) e c), lo sviluppo piano del poliedro si riduce ad un triangolo per il quale il
calcolo della caratteristica di Eulero è molto facile dato che V = 3, S = 3 e
F = 2 (contando, come detto all’inizio della dimostrazione, sia la faccia interna
che quella esterna). Pertanto F − S + V = 2 − 3 + 3 = 2. ◭—
La formula della caratteristica di Eulero per un politopo n-dimensionale si
generalizza nella seguente (Formula di Schläfli)
viso
N0 − N1 + N2 − · · · + (−1)n−1 · Nn−1 = 1 − (−1)n
ove Nj , 0 ≤ j < n è il numero dei politopi j-dimensionali contenuti nel politopo; si può dimostrare che essa risulta invariante per trasformazioni continue.
Tale formula consente anche di “memorizzare” più facilmente quella di Eulero,
osservando che il numero di politopi di dimensione pari va sommato, mentre
va sottratto il numero di politopi di dimensione dispari.
za p
rov
Infine, per completezza, ricordiamo che un importantissimo risultato sulle
triangolazioni delle superfici compatte dovuto a Radò consente di classificare
tali oggetti passando allo studio degli sviluppi piani dei poliedri associati.
Vediamo ora come usando il Teorema di Eulero sia possibile ricavare in altro
modo i solidi platonici. Sia infatti dato un poligono convesso regolare {p, q};
poiché ogni spigolo appartiene a due facce e unisce due vertici si ricavano
subito le seguenti relazioni
2S = pF = qV.
Pertanto, utilizzando la Formula di Eulero si deduce che
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
2=F −S+V =
cioè anche
p. 442
2·S
2·S
−S+
p
q
1 1
1
1
+ = + .
p q
2 S
(B.3)
Essendo per ipotesi p, q numeri interi maggiori di 3 (e S > 0), se p e q sono
strettamente maggiori di 3 si ottiene l’assurdo
1 1
1
1
1
1 1
+ ≤ + = ≤ + .
p q
4 4
2
2 S
Quindi o p = 3 o q = 3. Se p = 3, da
1
1 1 1
= + −
S
q
3 2
0<
ria
si ricava che q ≤ 5, cioè q = 3 o q = 4 o q = 5. Poiché la (B.3) è “simmetrica”
in p e q, si vede facilmente che, oltre alle coppie viste, le uniche altre possibili
soluzioni intere di (B.3) sono p = 4, q = 3 e p = 5, q = 3. Le caratteristiche
dei solidi platonici sono riassunte nella tabella B.1.
Tabella B.1. Caratteristiche dei solidi platonici
F S V
tetraedro 4 6 4
ottaedro 8 12 6
icosaedro 20 30 12
cubo
6 12 8
dodecaedro 12 30 20
za p
rov
{3, 3}
{3, 4}
{3, 5}
{4, 3}
{5, 3}
nome
viso
tipo {p, q}
Richiami sulle simmetrie
Indicata con d la distanza euclidea in IRN una funzione biunivoca f : IRN →
IRN tale che ∀x, y ∈ IRN
d(f (x), f (y)) = ρ · d(x, y)
boz
©F. Rosso, Università di Firenze
ρ ∈ IR+
www.math.unifi.it/rosso/
p. 443
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
si dice una similitudine o trasformazione di similitudine di rapporto ρ. In
particolare se ρ = 1 la trasformazione si dice isometria, mentre sarà un ingrandimento o una riduzione a seconda che ρ > 1 o ρ < 1. In IR2 un esempio
di similitudine è un’omotetia di centro O e rapporto ρ, cioè una applicazione
del piano in sé che lascia fisso il punto O e trasforma ogni altro punto nel
modo indicato nella figura B.10, mentre un esempio di isometria del piano
è una simmetria assiale o riflessione (cioè una applicazione del piano in sé
involutoria che lascia fisso ogni punto di una retta fissata detta asse di simmetria e che trasforma ogni semipiano individuato dall’asse nell’altro. Anche
le traslazioni e le rotazioni del piano sono isometrie.
P′
ρ · d(O, P )
P
O
viso
ria
Figura B.10. Esempio di omotetia di centro O e rapporto ρ; il punto P ′ viene
individuato sulla congiungente OP alla distanza d(O, P ′ ) = ρ · d(O, P ).
za p
rov
Figura B.11. Esempio di simmetria assiale.
È facile vedere che:
ogni traslazione del piano si può ottenere come composizione di due riflessioni ad assi paralleli (si noti che l’intensità della traslazione è pari al
doppio della distanza fra gli assi);
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
p. 444
Figura B.12. Traslazione
ogni rotazione del piano si può ottenere come composizione di due riflessioni ad assi incidenti nel centro di rotazione (si noti che l’angolo della
rotazione è pari al doppio dell’angolo fra gli assi);
viso
ria
Figura B.13. Rotazione
ogni similitudine del piano si può ottenere come composizione di al più
un’omotetia, di una traslazione e di una rotazione, ossia ogni similitudine
del piano si può ottenere come composizione di al più un’omotetia e di
quattro riflessioni.
za p
rov
Le roto-traslazioni vengono anche dette movimenti rigidi del piano. L’insieme
dei movimenti rigidi e delle riflessioni del piano si dicono anche congruenze.
Si noti che l’insieme delle rotazioni di centro fissato (cosı̀ come l’insieme di
tutte le traslazioni del piano), con la ovvia legge di composizione, costitui-
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
p. 445
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
scono un gruppo6 . Diremo che un oggetto o figura è “simmetrica” se esiste
una congruenza che lascia l’oggetto invariato pur permutando i suoi elementi.
L’insieme di tutte le congruenze di un oggetto simmetrico (a cui va aggiunto
l’identità) è un gruppo detto gruppo delle simmetrie dell’oggetto. Più ampio è
tale gruppo e maggiori sono le simmetrie dell’oggetto, nel senso che l’oggetto
appare più simmetrico (si noti che ogni oggetto ha per simmetria l’identità).
Osserviamo in particolare che se il gruppo delle simmetrie di una figura è
finito, la figura possiede un numero finito di “vertici” che vengono permutati
dalle congruenze. Pertanto esiste un “centro” che viene trasformato in sé dalle
congruenze. Dunque abbiamo mostrato la seguente
Ogni gruppo finito di congruenze lascia almeno un punto fisso.
viso
ria
In particolare se il gruppo finito delle congruenze di una figura è ciclico (il che
accade se ogni congruenza S del gruppo si ottiene componendo m volte con se
stessa una sola congruenza T del gruppo, detta generatore del gruppo) il punto
A della figura verrà trasformato nel punto A1 = T (A) o in A2 = T (A1 ) =
T (T (A)) o nel punto A−1 = T −1 (A) o, in generale, nel punto Ak = T k (A) con
−n < k < n dalle congruenze del gruppo di simmetrie della figura. I punti
A−n+1 , . . . , A−1 , A, A1 , . . . , An−1 possono essere pensati come vertici di
un poligono che risulta equilatero (si ricordi che T è un’isometria). Viceversa,
dato un poligono regolare di n lati, esso è dotato di un gruppo di simmetrie che
ha come sottogruppo il gruppo delle rotazioni aventi per centro il centro del
poligono: esso è un gruppo ciclico generato dalla rotazione di ampiezza 2π/n.
Passando dal piano allo spazio, una rotazione attorno ad una retta o asse
di ampiezza 2π/n determina un gruppo ciclico di n elementi (considerando
anche l’identità). L’asse è detto binario, ternario, quaternario, ecc. a seconda
che n = 2, 3, 4, ecc.
6
za p
rov
Vogliamo ora computare il numero di rotazioni di un poliedro {p, q}. I possibili
assi di rotazione sono le congiungenti il centro del poliedro con i vertici, i punti
medi degli spigoli e i centri delle facce. Poiché, a parte il tetraedro, vertici,
spigoli e facce sono antipodali rispetto al centro del poliedro, il numero degli
assi è 12 (F + S + V ); nel tetraedro, però, ogni vertice è antipodale ad una
faccia, sicché il numero totale degli assi continua ad essere 21 (F + S + V ). In
un poliedro {p, q}, attorno ad ogni asse passante per un vertice si determinano
q − 1 rotazioni (non computando l’identità), ovvero ogni asse per un vertice
di un poliedro {p, q} è q-nario, mentre ogni asse passante per il centro di una
In matematica si indica con tale nome un insieme di oggetti in cui sia definita
una legge di moltiplicazione (che possiamo indicare ad esempio col simbolo ◦)
con le seguenti proprietà: il “prodotto” (comunque sia definito) di due elementi
a, b dell’insieme genera un elemento c appartenete all’insieme stesso, il prodotto
è associativo (cioè (a ◦ b) ◦ c = a ◦ (b ◦ c)), esiste un elemento neutro e (tale cioè
che a ◦ e = a), per ogni elemento a esiste l’inverso ã (ovvero a ◦ ã = e).
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
p. 446
faccia è p-nario (le p rotazioni attorno ad un asse passante per il centro di
una faccia coincidono infatti col gruppo delle rotazioni della faccia stessa, che
è un poligono regolare con p lati). Gli assi passanti per il punto medio di
uno spigolo sono invece binari. In totale dunque, escludendo di computare
l’identità, il numero delle rotazioni di un poliedro {p, q} è pari a
1
(F (p − 1) + S + V (q − 1)).
2
Tenendo conto della formula di Eulero e delle relazioni 2S = pF = qV che
sussistono in un poliedro {p, q} risulta poi
1
1
(F (p − 1) + S + V (q − 1)) = (pF − F + S + qV − V ) =
2
2
=
1
1
(pF − 2 + qV ) = (4S − 2) = 2S − 1.
2
2
za p
rov
viso
ria
Pertanto, il numero delle rotazioni di un poliedro {p, q}, contando anche l’identità, è dato da 2S. Lo studio delle simmetrie dei poliedri è alla base della
classificazione delle forme semplici dei cristalli (cristallografia geometrica). I
cristalli infatti presentano una eccezionale regolarità e simmetria e sono raggruppati in 32 classi che si possono suddividere in 7 sistemi a seconda delle
proprietà di simmetria. Cosı̀ il sistema cubico (quello della comune salgemma)
è caratterizzato dall’esistenza di 3 assi quaternari e 4 ternari (nella più regolare delle classi, la esacisottaedrica, vi sono anche 6 assi binari, a conferma della
formula appena calcolata, dato che 6+4(3−1)+3(4−1)+1 = 24 = 2·12 = 2S),
nel sistema esagonale i cristalli sono dotati di un asse senario, in quello tetragonale di un asse quaternario, in quello trigonale di un asse ternario, in
quello rombico di un asse binario; infine il sistema monoclino è caratterizzato dalla presenza di una simmetria di tipo “riflessione rispetto ad un piano”
mentre quello triclino non ha alcuna simmetria. Salta agli occhi che queste
simmetrie (e tutte le possibili loro combinazioni) sono poche se confrontate
con quelle immaginabili per i poliedri o per altre strutture naturali. Si pensi
ad una stella marina: se le cinque braccia sono uguali essa è dotata di una
simmetria di asse quinario. In natura invece non esistono cristalli con assi
quinari, né con assi di simmetria di tipo settenario, ottonari o, in generale,
maggiore di senario. Il motivo è profondo ed interessante dal punto di vista
geometrico. Fu lo studioso francese Haüy il primo a supporre (nel 1784) che
i cristalli fossero formati da un aggregato regolare di piccolissime “celle” la
cui forma geometrica determinava quella del cristallo stesso. Haüy chiamò tali
celle molecole integranti e, benché ne avesse individuato solo tre, egli tuttavia
introdusse l’idea che i cristalli avessero una struttura regolare e discontinua
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
p. 447
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
che si sarebbe poi sviluppata fino all’odierno concetto di reticolo cristallino
di atomi, definitivamente confermato nel 1912 con l’esperimento di diffrazione
dei raggi X ideato da Max von Laue. Ben prima però, l’intuizione di Haüy
fu perfezionata da Bravais il quale, studiando i possibili modi in cui si potevano realizzare dei reticoli spaziali omogenei, periodici e discontinui, riuscı̀ a
trovare 14 possibili reticoli, che, tenendo conto delle simmetrie, si riducono
ai 7 sistemi già descritti. L’idea di Haüy di molecola integrante consentı̀ al
mineralogista inglese Miller di associare a ogni faccia di (una cella di) un cristallo dei simboli (noti come simboli milleriani (l : m : n)) che, rispetto ad un
opportuno sistema di riferimento cristallografico, rappresentano i coefficienti
(normalizzati) che individuano il piano contenente la faccia stessa. Poiché si
ritiene che un cristallo sia una struttura discontinua e periodica, se ne deduce
che deve valere la cosiddetta legge di razionalità degli indici, secondo la quale a
facce parallele corrispondono, rispetto ad un opportuno sistema di riferimento
cristallografico, indici milleriani proporzionali, con costante di proporzionalità
razionale. Tale legge fondamentale della cristallografia è anche detta legge di
Haüy.
viso
ria
Sulla base di queste premesse cristallografiche possiamo mostrare geometricamente il motivo per il quale nei cristalli non possono esistere altri assi di
rotazione oltre a quelli di tipo binario, ternario, quaternario e senario. Sia dato
infatti un reticolo piano di punti dotato di più di un centro di rotazione. Sia
P un centro di rotazione di ampiezza 2π/n e sia Q 6= P un centro di rotazione
di ampiezza 2π/n che realizzi la minima distanza r da P (si veda la figura
B.14). Sia P ′ il trasformato di P rispetto alla rotazione di centro Q e Q′ il
trasformato di Q rispetto alla rotazione di centro P ′ . Possono presentarsi due
eventualità: o P = Q′ oppure P 6= Q′ . Nel primo caso il triangolo di vertici
P ′ , Q e P = Q′ è equilatero e dunque l’angolo di rotazione è di π/3, ossia
n = 6; nel secondo caso dovendo risultare, per ipotesi su r, d(P, Q) ≤ d(P, Q′ )
segue immediatamente che l’angolo di rotazione deve essere maggiore di π/2,
ossia n ≤ 4.
za p
rov
Q’
2π/n
P’
P
2π/n
Q
Figura B.14. Dimostrazione geometrica della restrizione cristallografica
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
p. 448
Questa dimostrazione è dovuta a Wigner e il risultato è anche noto come restrizione cristallografica; si osservi che è in perfetto accordo con il risultato
sulla tassellatura del piano e che, in cristallografia, si interpreta con la proprietà di omogeneità dei cristalli. Per la precisione, va ricordato che esistono
degli stati di aggregazione atomica con una struttura diversa (detta dei quasicristalli) da quella dei cristalli che non implicano l’esistenza di un reticolo e per
le quali esistono delle simmetrie di ordine 5. Queste strutture, rivelate dalla
diffrazione ai raggi X di una lega di alluminio e manganese, vennero scoperte
per la prima volta nel 1984, ma descritte molto prima, come ipotesi teorica,
dal matematico inglese Roger Penrose che studiò la possibilità di tassellare il
piano con forme pentagonali in maniera non periodica.
Classi cristalline
descrizione
I 3 assi della croce assiale hanno tutti differente
lunghezza e formano tra loro angoli diversi da
90◦ . I cristalli triclini non presentano né assi di
simmetria né piani di riflessione
Sistema monoclino
I 3 assi della croce assiale sono di diversa lunghezza. 2 assi formano tra loro angoli retti; il
terzo forma con il loro piano un angolo maggiore di 90◦ . I cristalli monoclini hanno un solo
asse binario ed un solo piano di simmetria
viso
Sistema ortorombico
ria
Classe
Sistema triclino
I 3 assi della croce assiale hanno lunghezza differente e formano tra loro 3 angoli retti. Si
considera ortorombico un cristallo che presenta
solo assi binari e/o 2 piani di riflessione insieme
za p
rov
Sistema trigonale o romboedrico La croce assiale è a quattro assi, 3 assi di uguale lunghezza giacciono su un piano orizzontale formando un angolo di 120◦ tra di loro. Il
quarto asse è più lungo o più corto degli altri
ed è perpendicolare al loro piano orizzontale.
Un cristallo è trigonale se ha un asse ternario
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
p. 449
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
Due degli assi della croce assiale hanno eguale lunghezza in quanto a 90◦ l’asse si ripete
a causa della simmetria quaternaria, il terzo
è più lungo o più corto. Tutti e 3 gli angoli
che formano sono retti. Un cristallo si considera tetragonale se ha un solo asse di simmetria
quaternario
Sistema esagonale
Impiega una croce assiale a 4 assi. 3 assi di
uguale lunghezza giacciono sul piano orizzontale facendo un angolo di 120◦ l’uno con l’altro.
Il quarto asse è più lungo o più corto ed è disposto perpendicolarmente al piano degli altri
tre. È considerato esagonale un cristallo avente
un asse senario
Sistema cubico
Tutti e 3 gli assi della croce assiale hanno la
stessa lunghezza e si incrociano tra loro ad angolo retto. Si considera cubico un cristallo che
abbia almeno 2 assi di simmetria ternari
za p
rov
viso
ria
Sistema tetragonale
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/
p. 450
viso
ria
Fabio Rosso: Lezioni di Matematica ..., Capitolo B
za p
rov
Figura B.15. Reticoli di Bravais
boz
©F. Rosso, Università di Firenze
www.math.unifi.it/rosso/