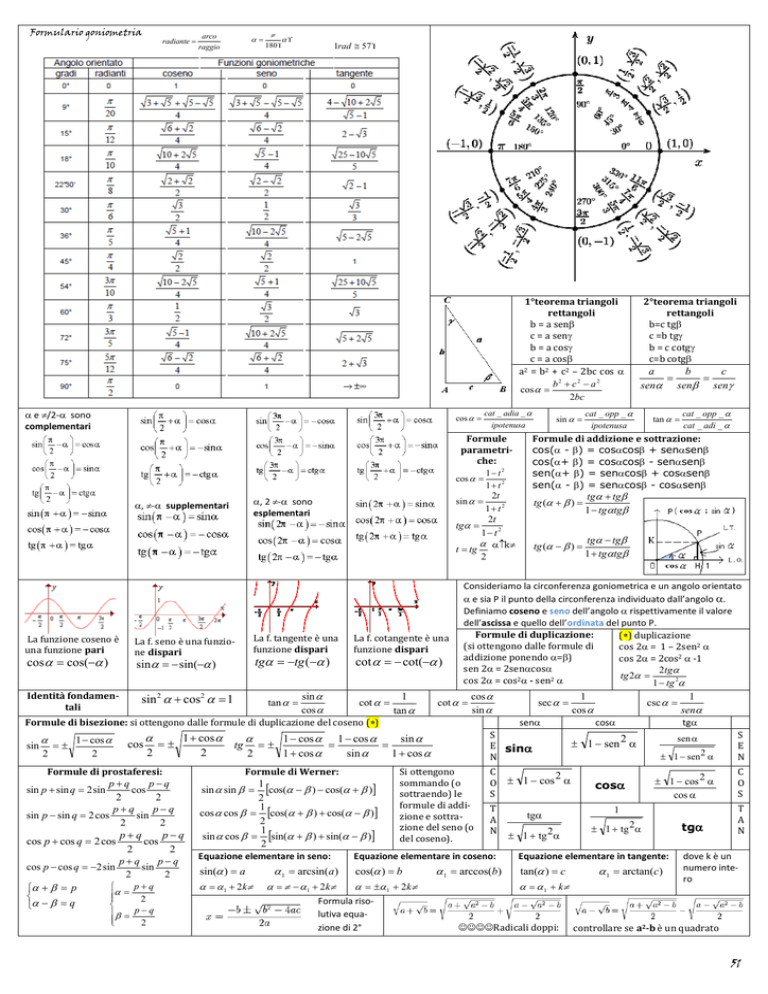
Formulario goniometria
radiante =
arco
raggio
α=
π
180°
α°
1rad ≅ 57°
1°teorema triangoli
rettangoli
b = a senβ
c = a senγ
b = a cosγ
c = a cosβ
a2 = b2 + c2 – 2bc cos α
b2 + c 2 − a 2
cos α =
2bc
α e π/2-α sono
complementari
cos α =
cat _ adia _ α
ipotenusa
Formule
parametriche:
1− t2
1+ t 2
2t
sin α =
1+ t2
cos α =
α, π-α supplementari
α, 2 π-α sono
esplementari
2t
1− t 2
α α≠kπ
t = tg
2
sin α =
cat _ opp _ α
ipotenusa
2°teorema triangoli
rettangoli
b=c tgβ
c =b tgγ
b = c cotgγ
c=b cotgβ
a
b
c
=
=
senα senβ senγ
tan α =
cat _ opp _ α
cat _ adi _ α
Formule di addizione e sottrazione:
cos(α - β) = cosαcosβ + senαsenβ
cos(α+ β) = cosαcosβ - senαsenβ
sen(α+ β) = senαcosβ + cosαsenβ
sen(α - β) = senαcosβ - cosαsenβ
tgα + tgβ
tg (α + β ) =
1 − tgαtgβ
tgα =
tg (α − β ) =
tgα − tgβ
1 + tgαtgβ
Consideriamo la circonferenza goniometrica e un angolo orientato
α e sia P il punto della circonferenza individuato dall’angolo α.
Definiamo coseno e seno dell’angolo α rispettivamente il valore
dell’ascissa e quello dell’ordinata del punto P.
Formule di duplicazione:
(∗) duplicazione
La f. tangente è una La f. cotangente è una
La funzione coseno è
La f. seno è una funzio(si ottengono dalle formule di
cos 2α = 1 – 2sen2 α
funzione dispari
funzione dispari
una funzione pari
ne dispari
addizione ponendo α=β)
cos 2α = 2cos2 α -1
tgα = −tg (−α )
cot α = − cot(−α )
cosα = cos(−α )
sin α = − sin(−α )
sen 2α = 2senαcosα
2tgα
tg 2α =
cos 2α = cos2α - sen2 α
1 − tg 2α
Identità fondamensin α
cos α
1
1
1
sin 2 α + cos2 α = 1
tan α =
cot α =
sec α =
csc α =
cot α =
tali
cos α
sin α
cos α
senα
tan α
Formule di bisezione: si ottengono dalle formule di duplicazione del coseno (∗)
senα
cosα
tgα
S
S
α
1 + cos α
sen α
1 − cos α 1 − cos α
sin α
α
α
1 − cos α
± 1 − sen 2 α
cos = ±
tg = ±
=
=
sin = ±
E sinα
E
2
2
2
1 + cos α
sin α
1 + cos α
2
2
± 1 − sen 2 α
N
N
Formule di prostaferesi:
p+q
p−q
sin p + sin q = 2 sin
cos
2
2
p+q
p−q
sin p − sin q = 2 cos
sin
2
2
cos p + cos q = 2 cos
cos p − cos q = −2 sin
α + β = p
α − β = q
p+q
p−q
cos
2
2
p+q
p−q
sin
2
2
p+q
α=
2
β = p − q
2
Formule di Werner:
Si ottengono
C
C
2
± 1 − cos 2 α
sommando (o
O ± 1 − cos α
O
1
cos
α
sin α sin β = [cos(α − β ) − cos(α + β )]
sottraendo) le
S
S
cos α
2
formule di addi1
T
T
1
cos α cos β = [cos(α + β ) + cos(α − β )]
tgα
zione e sottraA
A
2
2
zione
del
seno
(o
tgα
± 1 + tg α
1
N
N
2α
±
1
+
tg
sin α cos β = [sin(α + β ) + sin(α − β )]
del coseno).
2
Equazione elementare in seno:
Equazione elementare in coseno:
Equazione elementare in tangente: dove k è un
numero intesin(α ) = a
α 1 = arcsin(a ) cos(α ) = b
α 1 = arccos(b)
tan(α ) = c
α 1 = arctan(c)
ro
α = α 1 + 2kπ α = π − α 1 + 2kπ
α = ±α 1 + 2kπ
α = α 1 + kπ
Formula risolutiva equazione di 2°
☺☺☺☺Radicali doppi:
controllare se a2-b è un quadrato
51










