LA DISTRIBUZIONE NORMALE o DI GAUSS

LA DISTRIBUZIONE NORMALE o DI GAUSS
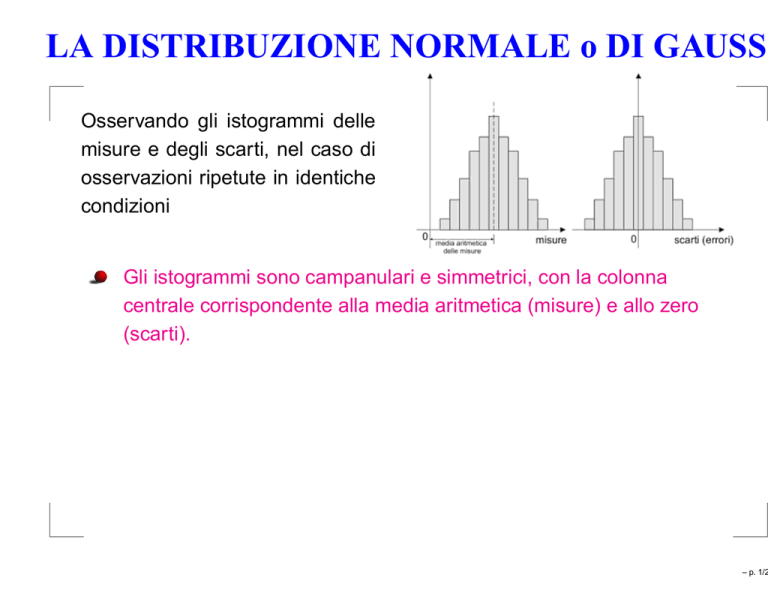
Osservando gli istogrammi delle
misure e degli scarti, nel caso di
osservazioni ripetute in identiche
condizioni
Gli istogrammi sono campanulari e simmetrici, con la colonna
centrale corrispondente alla media aritmetica (misure) e allo zero
(scarti).
– p. 1/2
LA DISTRIBUZIONE NORMALE o DI GAUSS
Osservando gli istogrammi delle
misure e degli scarti, nel caso di
osservazioni ripetute in identiche
condizioni
Gli istogrammi sono campanulari e simmetrici, con la colonna
centrale corrispondente alla media aritmetica (misure) e allo zero
(scarti).
Le misure prossime alla media sono più numerose di quelle lontane.
Gli scarti più piccoli sono più numerosi di quelli grandi.
– p. 1/2
LA DISTRIBUZIONE NORMALE o DI GAUSS
Osservando gli istogrammi delle
misure e degli scarti, nel caso di
osservazioni ripetute in identiche
condizioni
Gli istogrammi sono campanulari e simmetrici, con la colonna
centrale corrispondente alla media aritmetica (misure) e allo zero
(scarti).
Le misure prossime alla media sono più numerose di quelle lontane.
Gli scarti più piccoli sono più numerosi di quelli grandi.
Il numero delle misure maggiori della media è all’incirca uguale a
quello delle misure minori della media. Il numero deli scarti positivi (in
eccesso) è all’incirca uguale a quello degli scarti negativi (in difetto).
– p. 1/2
LA DISTRIBUZIONE NORMALE o DI GAUSS
Osservando gli istogrammi delle
misure e degli scarti, nel caso di
osservazioni ripetute in identiche
condizioni
Gli istogrammi sono campanulari e simmetrici, con la colonna
centrale corrispondente alla media aritmetica (misure) e allo zero
(scarti).
Le misure prossime alla media sono più numerose di quelle lontane.
Gli scarti più piccoli sono più numerosi di quelli grandi.
Il numero delle misure maggiori della media è all’incirca uguale a
quello delle misure minori della media. Il numero deli scarti positivi (in
eccesso) è all’incirca uguale a quello degli scarti negativi (in difetto).
Una funzione analitica atta a rappresentare una tale distribuzione
deve essere simmetrica, unimodale e campanulare.
– p. 1/2
DISTRIBUZIONE DEGLI ERRORI ACCIDENTALI
Proprietà ipotetiche dedotte da Gauss dalle
osservazioni:
s = x − x∗ scarto di una misura dal valore vero
– p. 2/2
DISTRIBUZIONE DEGLI ERRORI ACCIDENTALI
Proprietà ipotetiche dedotte da Gauss dalle
osservazioni:
s = x − x∗ scarto di una misura dal valore vero
1. Se s > 0 e s < 0 equiprobabili → distribuzione degli
scarti simmetrica rispetto allo zero.
– p. 2/2
DISTRIBUZIONE DEGLI ERRORI ACCIDENTALI
Proprietà ipotetiche dedotte da Gauss dalle
osservazioni:
s = x − x∗ scarto di una misura dal valore vero
1. Se s > 0 e s < 0 equiprobabili → distribuzione degli
scarti simmetrica rispetto allo zero.
2. Scarti piccoli più probabili: se |s1 | > |s2 | →
P (|s1 |) < P (|s2 |).
– p. 2/2
DISTRIBUZIONE DEGLI ERRORI ACCIDENTALI
Proprietà ipotetiche dedotte da Gauss dalle
osservazioni:
s = x − x∗ scarto di una misura dal valore vero
1. Se s > 0 e s < 0 equiprobabili → distribuzione degli
scarti simmetrica rispetto allo zero.
2. Scarti piccoli più probabili: se |s1 | > |s2 | →
P (|s1 |) < P (|s2 |).
3. Condizione di normalizzazione (ipotesi aggiuntiva)
Z +∞
f (s) ds = 1
−∞
– p. 2/2
DISTRIBUZIONE DEGLI ERRORI ACCIDENTALI
In base alle 3 ipotesi e dal principio della media
aritmetica a Gauss derivò che la distribuzione degli
scarti di misure affette da errori accidentali è descritta
2 2
h
−h
da: f (s) = √π e s funzione di Gauss o legge
normale di distribuzione degli errori
– p. 3/2
DISTRIBUZIONE DEGLI ERRORI ACCIDENTALI
Soddisfa alle 3 ipotesi iniziali:
– p. 4/2
DISTRIBUZIONE DEGLI ERRORI ACCIDENTALI
Soddisfa alle 3 ipotesi iniziali:
1. Forma a campana simmetrica rispetto a s = 0;
– p. 4/2
DISTRIBUZIONE DEGLI ERRORI ACCIDENTALI
Soddisfa alle 3 ipotesi iniziali:
1. Forma a campana simmetrica rispetto a s = 0;
2. Decrescente per |s| crescente;
– p. 4/2
DISTRIBUZIONE DEGLI ERRORI ACCIDENTALI
Soddisfa alle 3 ipotesi iniziali:
1. Forma a campana simmetrica rispetto a s = 0;
2. Decrescente per |s| crescente;
3. Tendente a zero per s → ±∞, come richiesto dalla
condizione di normalizzazione)
– p. 4/2
DISTRIBUZIONE DEGLI ERRORI ACCIDENTALI
Soddisfa alle 3 ipotesi iniziali:
1. Forma a campana simmetrica rispetto a s = 0;
2. Decrescente per |s| crescente;
3. Tendente a zero per s → ±∞, come richiesto dalla
condizione di normalizzazione)
La legge normale degli scarti dipende da un solo
parametro h, detto modulo di precisione della misura.
Tanto maggiore è h tanto minore è la dispersione delle
misure rispetto alla media.
– p. 4/2
DISTRIBUZIONE DEGLI ERRORI ACCIDENTALI
Soddisfa alle 3 ipotesi iniziali:
1. Forma a campana simmetrica rispetto a s = 0;
2. Decrescente per |s| crescente;
3. Tendente a zero per s → ±∞, come richiesto dalla
condizione di normalizzazione)
La legge normale degli scarti dipende da un solo
parametro h, detto modulo di precisione della misura.
Tanto maggiore è h tanto minore è la dispersione delle
misure rispetto alla media.
Per h descrecente la campana si abbassa e si allarga.
– p. 4/2
PROPRIETÀ DELLA LEGGE NORMALE
Hp: Supponiamo di aver infinite misure, N → ∞
– p. 5/2
PROPRIETÀ DELLA LEGGE NORMALE
Hp: Supponiamo di aver infinite misure, N → ∞
Valore di aspettazione dello variabile scarto:
+∞
h
sf (s)ds =
E(s) = √
π −∞
Z +∞
h
−h2 s2
√
ds = 0
se
π −∞
è identicamente nullo.
Z
– p. 5/2
PROPRIETÀ DELLA LEGGE NORMALE
Hp: Supponiamo di aver infinite misure, N → ∞
Valore di aspettazione dello variabile scarto:
+∞
h
sf (s)ds =
E(s) = √
π −∞
Z +∞
h
−h2 s2
√
ds = 0
se
π −∞
è identicamente nullo.
Z
Ne segue un’importantissima conseguenza:
E(s) = E (x − x∗ ) = E(x) − x∗ = 0 → E(x) = x∗
– p. 5/2
PROPRIETÀ DELLA LEGGE NORMALE
E(x) = x∗
– p. 6/2
PROPRIETÀ DELLA LEGGE NORMALE
E(x) = x∗
Il valore di aspettazione delle misure di una grandezza
fisica affette solo da errori casuali esiste, e coincide con
il valore vero della grandezza misurata.
– p. 6/2
PROPRIETÀ DELLA LEGGE NORMALE
ERRORE MEDIO θ: il valore di
aspettazione del
modulo dello scarto θ = E |s|
1
θ= √
h π
– p. 7/2
PROPRIETÀ DELLA LEGGE NORMALE
ERRORE MEDIO θ: il valore di
aspettazione del
modulo dello scarto θ = E |s|
1
θ= √
h π
ERRORE PROBABILE ρ: quel valore di s per cui metà
delle misure ha |s| ≤ ρ
Z +ρ
f (s)ds = 0.5
−ρ
– p. 7/2
PROPRIETÀ DELLA LEGGE NORMALE
ERRORE MEDIO θ: il valore di
aspettazione del
modulo dello scarto θ = E |s|
1
θ= √
h π
ERRORE PROBABILE ρ: quel valore di s per cui metà
delle misure ha |s| ≤ ρ
Z +ρ
f (s)ds = 0.5
−ρ
ERRORE QUADRATICO MEDIO σ : è la radice
quadrata del valore di aspettazione del quadrato degli
1
1
2
scarti ( E s = 2h2 ) σ = √
2h
– p. 7/2
RELAZIONI TEORICHE
Per misure affette da errori distribuiti secondo la legge
normale:
l’errore quadratico medio ed il modulo di precisione h
soddisfano alla relazione σ =
1
√
h 2
– p. 8/2
RELAZIONI TEORICHE
Per misure affette da errori distribuiti secondo la legge
normale:
l’errore quadratico medio ed il modulo di precisione h
soddisfano alla relazione σ =
1
√
h 2
Il rapporto tra errore probabile ed errore quadratico
medio vale σρ ≃ 0.674
– p. 8/2
RELAZIONI TEORICHE
Per misure affette da errori distribuiti secondo la legge
normale:
l’errore quadratico medio ed il modulo di precisione h
soddisfano alla relazione σ =
1
√
h 2
Il rapporto tra errore probabile ed errore quadratico
medio vale σρ ≃ 0.674
Il rapporto tra errore medio ed errore quadratico medio
vale
θ
σ
≃ 0.798
– p. 8/2
RELAZIONI TEORICHE
– p. 9/2
DISTRIBUZIONI DELLE MISURE E DEGLI SCARTI
Esprimendo h in funzione di σ la legge di Gauss diventa
f (s) =
√1
σ 2π
s2
−
e 2σ 2
– p. 10/2
DISTRIBUZIONI DELLE MISURE E DEGLI SCARTI
Esprimendo h in funzione di σ la legge di Gauss diventa
f (s) =
√1
σ 2π
s2
−
e 2σ 2
Esprimendo s = x − µ otteniamo f (x) =
√1
σ 2π
1
−
e 2
x−µ 2
σ
– p. 10/2
DISTRIBUZIONI DELLE MISURE E DEGLI SCARTI
Esprimendo h in funzione di σ la legge di Gauss diventa
f (s) =
√1
σ 2π
s2
−
e 2σ 2
Esprimendo s = x − µ otteniamo f (x) =
√1
σ 2π
1
−
e 2
x−µ 2
σ
– p. 10/2
LO SCARTO NORMALIZZATO
Essendo la distribuzione normale largamente utilizzata
e non avendo il suo integrale indefinito una forma
analitica, per il calcolo delle probabilità vengono usati
valori pre-tabulati.
– p. 11/2
LO SCARTO NORMALIZZATO
Essendo la distribuzione normale largamente utilizzata
e non avendo il suo integrale indefinito una forma
analitica, per il calcolo delle probabilità vengono usati
valori pre-tabulati.
Impossibile avere tabelle per tutte le possibili coppie di
valori dei parametri σ e µ. È quindi conveniente rendere
il calcolo della funzione cumulativa F (x) indipendente
dai parametri.
– p. 11/2
LO SCARTO NORMALIZZATO
Essendo la distribuzione normale largamente utilizzata
e non avendo il suo integrale indefinito una forma
analitica, per il calcolo delle probabilità vengono usati
valori pre-tabulati.
Impossibile avere tabelle per tutte le possibili coppie di
valori dei parametri σ e µ. È quindi conveniente rendere
il calcolo della funzione cumulativa F (x) indipendente
dai parametri.
Definiamo scarto normalizzato o variabile normale
x−µ
standardizzata t =
σ
– p. 11/2
LO SCARTO NORMALIZZATO
Essendo la distribuzione normale largamente utilizzata
e non avendo il suo integrale indefinito una forma
analitica, per il calcolo delle probabilità vengono usati
valori pre-tabulati.
Impossibile avere tabelle per tutte le possibili coppie di
valori dei parametri σ e µ. È quindi conveniente rendere
il calcolo della funzione cumulativa F (x) indipendente
dai parametri.
Definiamo scarto normalizzato o variabile normale
x−µ
standardizzata t =
σ
La densità di probabilità della variabile t è
1 − 1 t2
ϕ(t) = √ e 2
2π
– p. 11/2
DISTRIBUZIONE NORMALE STANDARDIZZATA
Indipendente dall’errore quadratico medio, ovvero dalla
precisione della misura.
– p. 12/2
DISTRIBUZIONE NORMALE STANDARDIZZATA
Indipendente dall’errore quadratico medio, ovvero dalla
precisione della misura.
La distribuzione normale standardizzata è una
particolare normale con E(x) = 0 e σ = 1.
1 − 1 t2
ϕ(t) = √ e 2
2π
– p. 12/2
DISTRIBUZIONE NORMALE STANDARDIZZATA
Alla normale standardizzata può essere ricondotta qualunque
x−µ
funzione di Gauss, effettuando il cambio di variabili: t =
σ
Z z
Z µ+zσ
1 x−µ 2
1 − 1 t2
1
√ e− 2 σ
√ e 2 dt =
valendo la relazione:
2π
−z
µ−zσ σ 2π
– p. 13/2
DISTRIBUZIONE NORMALE STANDARDIZZATA
Alla normale standardizzata può essere ricondotta qualunque
x−µ
funzione di Gauss, effettuando il cambio di variabili: t =
σ
Z z
Z µ+zσ
1 x−µ 2
1 − 1 t2
1
√ e− 2 σ
√ e 2 dt =
valendo la relazione:
2π
−z
µ−zσ σ 2π
Esistono delle tabelle per il calcolo dell’integrale della distribuzione
normale standardizzata
– p. 13/2
DISTRIBUZIONE NORMALE STANDARDIZZATA
Alla normale standardizzata può essere ricondotta qualunque
x−µ
funzione di Gauss, effettuando il cambio di variabili: t =
σ
Z z
Z µ+zσ
1 x−µ 2
1 − 1 t2
1
√ e− 2 σ
√ e 2 dt =
valendo la relazione:
2π
−z
µ−zσ σ 2π
Esistono delle tabelle per il calcolo dell’integrale della distribuzione
normale standardizzata
La distribuzione normale standardizzata presenta le stesse
caratteristiche della distribuzione normale NON standardizzata. Ciò
che distingue le due distribuzioni è che la normale standardizzata ha
µ = 0 e σ = 1.
– p. 13/2
DISTRIBUZIONE NORMALE STANDARDIZZATA
L’aspetto più importante della standardizzazione è che
trasformando una distribuzione normale di parametri
(µ, σ ) nella distribuzione standardizzata (0, 1), le aree
individuate nella prima da due qualsiasi ascisse x1 e x2
sono uguali alle aree individuate nella seconda dagli
scarti normalizzati
x1 − µ
x2 − µ
t1 =
t2 =
σ
σ
– p. 14/2
DISTRIBUZIONE NORMALE STANDARDIZZATA
La distribuzione normale standardizzata è
rappresentata da UNA SOLA CURVA, mentre la
distribuzione normale generale è costituita da una
famiglia a seconda dei valori di µ e σ .
– p. 15/2
LO SCARTO
NORMALIZZATO
Z
+1
Pr t ∈ [−1, +1]
Pr t ∈ [−2, +2]
Pr t ∈ [−3, +3]
=
=
=
√1
2π
√1
2π
2
− t2
√1
2π
e
Z−1
+2
Z−2
+3
2
− t2
e
2
− t2
e
dt = 0.6827 . . .
dt = 0.9545 . . .
dt = 0.9973 . . .
−3
– p. 16/2
LO SCARTO NORMALIZZATO
Ricordando che t = s/σ
Pr s ∈ [−σ, +σ]
≡ Pr t ∈ [−1, +1] ≈ 0.6827
Pr s ∈ [−2σ, +2σ] ≡ Pr t ∈ [−2, +2] ≈ 0.9545
Pr s ∈ [−3σ, +3σ] ≡ Pr t ∈ [−3, +3] ≈ 0.9973
– p. 17/2
INTERPRETAZIONE PROBABILISTICA DI σ
Le misure affette da errori casuali (e quindi normali)
hanno una probabilità del 68% di cadere all’interno di
un intervallo di semiampiezza σ centrato sul valore vero
della grandezza misurata. Il 95% e il 99,7% (quasi la
totalità) delle misure sono affette da errore in modulo
minore o al piu‘ uguale a 2σ e 3σ rispettivemente.
– p. 18/2
INTERPRETAZIONE PROBABILISTICA DI σ
Le misure affette da errori casuali (e quindi normali)
hanno una probabilità del 68% di cadere all’interno di
un intervallo di semiampiezza σ centrato sul valore vero
della grandezza misurata. Il 95% e il 99,7% (quasi la
totalità) delle misure sono affette da errore in modulo
minore o al piu‘ uguale a 2σ e 3σ rispettivemente.
L’intervallo di semiampiezza σ centrato su di una misura
qualsiasi di un campione ha pertanto una probabilità
del 68% di contenere il valore vero, sempreché gli errori
siano casuali e normali.
– p. 18/2
ESAME DEI DATI: criterio del 3σ
In una serie di misure dirette quale criterio per
individuare dati sospetti e anomali?
– p. 19/2
ESAME DEI DATI: criterio del 3σ
In una serie di misure dirette quale criterio per
individuare dati sospetti e anomali?
Si calcolano x e σx
– p. 19/2
ESAME DEI DATI: criterio del 3σ
In una serie di misure dirette quale criterio per
individuare dati sospetti e anomali?
Si calcolano x e σx
Si eliminano le misure |x − x̄| > 3σ (p ∼ 0.003).
– p. 19/2
ESAME DEI DATI: criterio del 3σ
In una serie di misure dirette quale criterio per
individuare dati sospetti e anomali?
Si calcolano x e σx
Si eliminano le misure |x − x̄| > 3σ (p ∼ 0.003).
Si ricalcolano x e σx
– p. 19/2
STIMA DELL’ERRORE QUADRATICO MEDIO
Si abbiano n misure xi di una stessa grandezza fisica
– p. 20/2
STIMA DELL’ERRORE QUADRATICO MEDIO
Si abbiano n misure xi di una stessa grandezza fisica
Sia ǫi = xi − x∗ l’errore di una misura, dove x∗ è il valore vero
(incognito) della grandezza fisica in esame.
– p. 20/2
STIMA DELL’ERRORE QUADRATICO MEDIO
Si abbiano n misure xi di una stessa grandezza fisica
Sia ǫi = xi − x∗ l’errore di una misura, dove x∗ è il valore vero
(incognito) della grandezza fisica in esame.
n
1X
Sia ǫ =
ǫi l’errore da associare alla media aritmetica.
n i=1
– p. 20/2
STIMA DELL’ERRORE QUADRATICO MEDIO
Si abbiano n misure xi di una stessa grandezza fisica
Sia ǫi = xi − x∗ l’errore di una misura, dove x∗ è il valore vero
(incognito) della grandezza fisica in esame.
n
1X
Sia ǫ =
ǫi l’errore da associare alla media aritmetica.
n i=1
Sia si = xi − x lo scarto di una misura rispetto alla media aritmetica.
– p. 20/2
STIMA DELL’ERRORE QUADRATICO MEDIO
Si abbiano n misure xi di una stessa grandezza fisica
Sia ǫi = xi − x∗ l’errore di una misura, dove x∗ è il valore vero
(incognito) della grandezza fisica in esame.
n
1X
Sia ǫ =
ǫi l’errore da associare alla media aritmetica.
n i=1
Sia si = xi − x lo scarto di una misura rispetto alla media aritmetica.
Ne segue che ǫi = si + ǫ.
– p. 20/2
STIMA DELL’ERRORE QUADRATICO MEDIO
Si abbiano n misure xi di una stessa grandezza fisica
Sia ǫi = xi − x∗ l’errore di una misura, dove x∗ è il valore vero
(incognito) della grandezza fisica in esame.
n
1X
Sia ǫ =
ǫi l’errore da associare alla media aritmetica.
n i=1
Sia si = xi − x lo scarto di una misura rispetto alla media aritmetica.
Ne segue che ǫi = si + ǫ.
Quadriamo: (ǫi )2 = (si )2 + ǫ2 + 2si ǫ
– p. 20/2
STIMA DELL’ERRORE QUADRATICO MEDIO
Si abbiano n misure xi di una stessa grandezza fisica
Sia ǫi = xi − x∗ l’errore di una misura, dove x∗ è il valore vero
(incognito) della grandezza fisica in esame.
n
1X
Sia ǫ =
ǫi l’errore da associare alla media aritmetica.
n i=1
Sia si = xi − x lo scarto di una misura rispetto alla media aritmetica.
Ne segue che ǫi = si + ǫ.
Quadriamo: (ǫi )2 = (si )2 + ǫ2 + 2si ǫ
Sommiamo da 1 a n
n
n
n
n
X
X
X
X
[(si )2 + ǫ2 + 2si ǫ] =
(ǫi )2 =
(si )2 + nǫ2 + 2ǫ
si
i=1
n
X
i=1
(ǫi )2 =
i=1
n
X
i=1
i=1
(si )2 + nǫ2
i=1
– p. 20/2
STIMA DELL’ERRORE
QUADRATICO
MEDIO
P
P
Dividiamo per n →
n
2
i=1 (ǫi )
n
=
n
2
i=1 (si )
n
+ ǫ2
– p. 21/2
STIMA DELL’ERRORE
QUADRATICO
MEDIO
P
P
Dividiamo per n →
n
2
i=1 (ǫi )
n
n
2
i=1 (si )
=
n
+ ǫ2
La varianza è dunque:
2
σ =
Pn
i=1 (si )
n
2
+ ǫ2
(1)
espressa in funzione degli scarti e dell’errore della media, ancora
incognito.
– p. 21/2
STIMA DELL’ERRORE
QUADRATICO
MEDIO
P
P
Dividiamo per n →
n
2
i=1 (ǫi )
n
n
2
i=1 (si )
=
n
+ ǫ2
La varianza è dunque:
2
σ =
Pn
i=1 (si )
n
2
+ ǫ2
(1)
espressa in funzione degli scarti e dell’errore della media, ancora
incognito.
Quadriamo l’errore
della media:
!
2
n
X
1
1
si
= 2 (ǫ1 + ǫ2 + · · · ǫn )2 =
ǫ2 = 2
n
n
i=1
1 2
2
2
(ǫ
+
ǫ
+
·
·
·
ǫ
1
2
n + 2ǫ1 ǫ2 + 2ǫ1 ǫ3 + · · · )
2
n
#
" n
1 X
2
ǫ = 2
(ǫi )2 + (2ǫ1 ǫ2 + 2ǫ1 ǫ3 + · · · )
n i=1
– p. 21/2
STIMA DELL’ERRORE
QUADRATICO
MEDIO
P
P
Dividiamo per n →
n
2
i=1 (ǫi )
n
n
2
i=1 (si )
=
n
+ ǫ2
La varianza è dunque:
2
σ =
Pn
i=1 (si )
n
2
+ ǫ2
(1)
espressa in funzione degli scarti e dell’errore della media, ancora
incognito.
Quadriamo l’errore
della media:
!
2
n
X
1
1
si
= 2 (ǫ1 + ǫ2 + · · · ǫn )2 =
ǫ2 = 2
n
n
i=1
1 2
2
2
(ǫ
+
ǫ
+
·
·
·
ǫ
1
2
n + 2ǫ1 ǫ2 + 2ǫ1 ǫ3 + · · · )
2
n
#
" n
1 X
2
ǫ = 2
(ǫi )2 + (2ǫ1 ǫ2 + 2ǫ1 ǫ3 + · · · )
n i=1
La somma dei termini misti può essere ragionevolmente posta = 0
per la simmetria della distribuzione di Gauss degli errori.
– p. 21/2
STIMA DELL’ERRORE QUADRATICO MEDIO
Il quadrato dell’errore della
 nmedia è quindi:
X
#
" n
(ǫi )2 

2
X


σ
1
1
i=1
=
(ǫi )2 = 
ǫ2 = 2

n i=1
n
n
n


– p. 22/2
STIMA DELL’ERRORE QUADRATICO MEDIO
Il quadrato dell’errore della
 nmedia è quindi:
X
#
" n
(ǫi )2 

2
X


σ
1
1
i=1
=
(ǫi )2 = 
ǫ2 = 2

n i=1
n
n
n


Introduciamo
questa relazione nell’ Eq. (1)
Pn
2
2
(s
)
σ
i
σ 2 = i=1
+
n
n
– p. 22/2
STIMA DELL’ERRORE QUADRATICO MEDIO
Il quadrato dell’errore della
 nmedia è quindi:
X
#
" n
(ǫi )2 

2
X


σ
1
1
i=1
=
(ǫi )2 = 
ǫ2 = 2

n i=1
n
n
n


Introduciamo
questa relazione nell’ Eq. (1)
Pn
2
2
(s
)
σ
i
σ 2 = i=1
+
n
n
Pn
Pn
2
2
(s
)
(s
)
1
i
i
→ σ 2 = i=1
= i=1
Esplicitiamo σ 2 → σ 2 1 −
n
n
n−1
– p. 22/2
STIMA DELL’ERRORE QUADRATICO MEDIO
Il quadrato dell’errore della
 nmedia è quindi:
X
#
" n
(ǫi )2 

2
X


σ
1
1
i=1
=
(ǫi )2 = 
ǫ2 = 2

n i=1
n
n
n


Introduciamo
questa relazione nell’ Eq. (1)
Pn
2
2
(s
)
σ
i
σ 2 = i=1
+
n
n
Pn
Pn
2
2
(s
)
(s
)
1
i
i
→ σ 2 = i=1
= i=1
Esplicitiamo σ 2 → σ 2 1 −
n
n
n−1
sP
n
2
i=1 (si )
Infine:
σ=
n−1
che esprime lo scarto quadratico medio in funzione di tutti e soli gli
scarti delle misure.
– p. 22/2
STIMA DELL’ERRORE QUADRATICO MEDIO DELLA MEDIA
L’errore della media o scarto quadratico medio della media deriva
dall’Eq. (??)
sP
r
n
2
σ2
σ
i=1 (si )
=√
σx =
σx =
n
n(n − 1)
n
– p. 23/2
STIMA DELL’ERRORE QUADRATICO MEDIO DELLA MEDIA
L’errore della media o scarto quadratico medio della media deriva
dall’Eq. (??)
sP
r
n
2
σ2
σ
i=1 (si )
=√
σx =
σx =
n
n(n − 1)
n
Il guadagno in precisione
all’aumentare del numero di
misure non scala linearmente
con n. Inoltre Il processo non
può essere spinto all’infinito:
interviene l’usura degli strumenti,
verificarsi di errori accidentali,
ecc.
– p. 23/2
INDETERMINAZIONI STATISTICHE
Nel caso di misure ripetute
lo scarto quadratico medio σm rappresenta
l’indeterminazione statistica da associare alla singola
misura. Infatti se prendiamo un qualunque misura mi , si
ha il ∼ 68% di probabilità che |mi − m| ≤ σm e cioè che
nell’intervallo
mi − σm | − − − − − −mi − −m − − − −|mi − σm
sia compreso il valore m assunto per vero.
– p. 24/2
INDETERMINAZIONI STATISTICHE
Nel caso di misure ripetute
lo scarto quadratico medio σm rappresenta
l’indeterminazione statistica da associare alla singola
misura. Infatti se prendiamo un qualunque misura mi , si
ha il ∼ 68% di probabilità che |mi − m| ≤ σm e cioè che
nell’intervallo
mi − σm | − − − − − −mi − −m − − − −|mi − σm
sia compreso il valore m assunto per vero.
lo scarto quadratico medio della media σm rappresenta
l’indeterminazione statistica da associare alla media
aritmetica. Essa è minore di quella della singola misura
di un fattore 1/n.
– p. 24/2
INDETERMINAZIONI STATISTICHE
Nel caso di misure ripetute
lo scarto quadratico medio σm rappresenta
l’indeterminazione statistica da associare alla singola
misura. Infatti se prendiamo un qualunque misura mi , si
ha il ∼ 68% di probabilità che |mi − m| ≤ σm e cioè che
nell’intervallo
mi − σm | − − − − − −mi − −m − − − −|mi − σm
sia compreso il valore m assunto per vero.
lo scarto quadratico medio della media σm rappresenta
l’indeterminazione statistica da associare alla media
aritmetica. Essa è minore di quella della singola misura
di un fattore 1/n.
– p. 24/2
TEOREMA DEL LIMITE CENTRALE
Hp: N variabili casuali xi , statisticamente indipendenti e provenienti
da una distribuzione avente densità di probabilità ignota, della quale
esistano finite sia la media µi che la varianza σi2 .
– p. 25/2
TEOREMA DEL LIMITE CENTRALE
Hp: N variabili casuali xi , statisticamente indipendenti e provenienti
da una distribuzione avente densità di probabilità ignota, della quale
esistano finite sia la media µi che la varianza σi2 .
Th: Una qualunque cobinazione lineare delle variabili con coefficienti
αi , tende asintoticamente alla distribuzione normale con media µ e
varianza σ 2 /N al crescere di N → ∞.
µ=
N
X
i=1
αi µi
σ2 =
N
X
αi2 σi2
i=1
– p. 25/2
TEOREMA DEL LIMITE CENTRALE
Hp: N variabili casuali xi , statisticamente indipendenti e provenienti
da una distribuzione avente densità di probabilità ignota, della quale
esistano finite sia la media µi che la varianza σi2 .
Th: Una qualunque cobinazione lineare delle variabili con coefficienti
αi , tende asintoticamente alla distribuzione normale con media µ e
varianza σ 2 /N al crescere di N → ∞.
µ=
N
X
i=1
αi µi
σ2 =
N
X
αi2 σi2
i=1
Nessuna ipotesi sulle distribuzioni delle variabili; unico requisito:
esistenza di media e varianza.
– p. 25/2
TEOREMA DEL LIMITE CENTRALE
Hp: N variabili casuali xi , statisticamente indipendenti e provenienti
da una distribuzione avente densità di probabilità ignota, della quale
esistano finite sia la media µi che la varianza σi2 .
Th: Una qualunque cobinazione lineare delle variabili con coefficienti
αi , tende asintoticamente alla distribuzione normale con media µ e
varianza σ 2 /N al crescere di N → ∞.
µ=
N
X
i=1
αi µi
σ2 =
N
X
αi2 σi2
i=1
Nessuna ipotesi sulle distribuzioni delle variabili; unico requisito:
esistenza di media e varianza.
Particolarizzando alla media aritmetica: x, tende asintoticamente alla
distribuzione normale con media µ e varianza σ 2 /N al crescere di N .
– p. 25/2
TEOREMA DEL LIMITE CENTRALE
– p. 26/2
TEOREMA DEL LIMITE CENTRALE
La figura precedente mostra il teorema del limite centrale all’opera. I
tre pannelli in alto mostrano tre distribuzioni continue di eventi
generati secondo una distribuzione normale (sinistra), uniforme
(centro) ed esponenziale (destra).
Successivamente (dall’alto verso il basso) sono mostrate le
distribuzioni delle medie di n variabili casuali estratte dalle due
distribuzioni. n vale, nell’ordine, 2, 5, 30.
Al crescere di n le distribuzioni della media tendono ad assumere
una forma regolare a campana, indipendentemente dalle distribuzioni
iniziali, fino a convergere a distribuzioni normali.
Da notare il secondo pannello centrale dall’alto (per n = 2). La forma
triangolare corrisponde, ad esempio, alla distribuzione della variabile
“somma del punteggio di due dadi”, già incontrata.
Visuallizza qui
– p. 27/2