ELEMENTI DI MICROECONOMIA PER L`APPLICAZIONE DELL

ELEMENTI DI MICROECONOMIA PER L'APPLICAZIONE DELL'ANALISI
ALL'ECONOMIA
1. LE FUNZIONI DI DOMANDA E DI OFFERTA
Si assume di dover osservare le vicende del mercato di un certo bene in un determinato periodo di
tempo. Le grandezze che intervengono in tale analisi sono i prezzi e le quantità della merce
scambiata in un certo numero di transazioni. Altri fattori che intervengono sono: la popolazione
totale della comunità presa a riferimento, i redditi pro-capite, il periodo dell'anno, i prezzi delle
merci negli altri mercati, ecc.; tutti questi fattori rientrano nelle cosiddette condizioni di mercato.
L'analisi delle funzioni di domanda e di offerta di un bene verrà effettuata attraverso il metodo di
analisi parziale. La caratteristica principale di tale metodo (sviluppato dall'economista Marshall) è
quella di postulare che nel corso dell'analisi di un particolare mercato le corrispondenti condizioni
di mercato restino immutate (ceteris paribus). Si consideri ad esempio il mercato del burro. La
domanda di burro dipende anche, in una certa misura, dal prezzo della margarina, essendo i due
beni succedanei. Una variazione nel prezzo della margarina può condurre ad una variazione del
prezzo del burro; in altri termini, le vicende del mercato del burro non sono indipendenti da quanto
accade sul mercato della margarina. Con l'assunto ceteris paribus vengono trascurati i collegamenti
tra i mercati. In un contesto di analisi parziale, le sole relazioni da assoggettare ad analisi sono
quelle tra il prezzo e la quantità domandata, da un lato, e tra prezzo e quantità offerta, dall'altro.
Con l'espressione domanda di un bene si intende la quantità dello stesso che i compratori
desiderano acquistare in corrispondenza ad un certo prezzo, in un certo istante. Scriveremo: D=D(p)
per denotare la funzione di domanda (parziale) del bene preso in considerazione. La funzione di
domanda è decrescente rispetto al prezzo.
Con offerta di un bene si intende la quantità dello stesso che gli individui (imprese produttrici del
bene o soggetti che ne sono in possesso) sono disposti a cedere in cambio del prezzo
corrispondente, in un dato istante. Indicando con S la somma delle quantità che i venditori sono
interessati a vendere al prezzo p, la scrittura S=S(p) denota la funzione di offerta (parziale) del
bene in questione. La funzione di offerta è una funzione crescente al crescere del prezzo.
2. La curva di domanda e di offerta
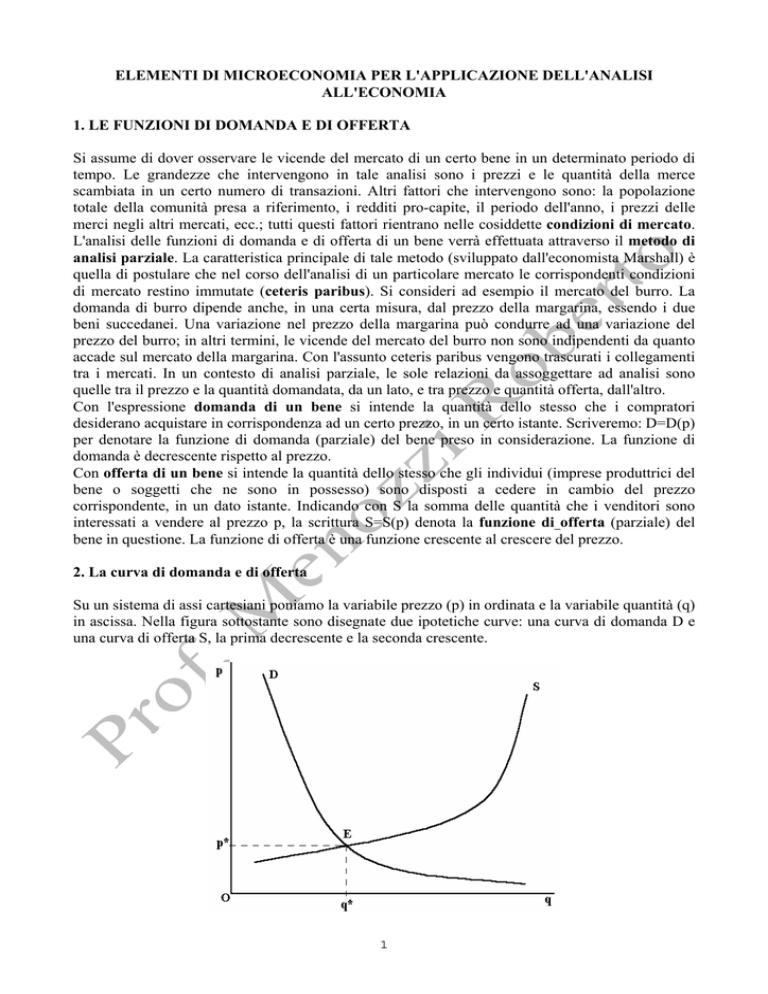
Su un sistema di assi cartesiani poniamo la variabile prezzo (p) in ordinata e la variabile quantità (q)
in ascissa. Nella figura sottostante sono disegnate due ipotetiche curve: una curva di domanda D e
una curva di offerta S, la prima decrescente e la seconda crescente.
1
Definiamo equilibrio di mercato (il punto E nel grafico sopra) lo stato in cui viene a trovarsi il
mercato di un particolare bene allorché, sotto un certo insieme di condizioni di mercato, la quantità
complessivamente domandata eguaglia la quantità complessivamente offerta. Il prezzo in
corrispondenza del quale tale eguaglianza si realizza è detto prezzo di equilibrio (il prezzo p* nel
grafico). In generale, non vi è alcuna ragione perché un equilibrio debba necessariamente esistere
come anche non è detto che, anche quando esiste, l'equilibrio debba essere unico.
3. ELASTICITÀ DI UNA FUNZIONE
Sia y=f(x) una funzione numerica definita in un intervallo I. Si chiama elasticità della funzione
f(x) in un punto x, dove sia y=f(x)≠0, la quantità:
x ∂y x ∂y ∂x
ε = f ′( x ) ⋅ =
⋅ =
:
y ∂x y
y x
ed esprime il limite, se esiste, degli incrementi relativi di y=f(x) e della variabile indipendente x.
4. ELASTICITÀ DELLA DOMANDA RISPETTO AL PREZZO
Nell'analisi della curva di domanda è importante avere a disposizione uno strumento che misuri di
quanto varia la quantità domandata al variare del prezzo, indipendentemente dalla scelta dell'unità
di misura con cui si esprimono prezzi e quantità. A ciò provvede la nozione di elasticità della
domanda rispetto al prezzo. Il concetto di elasticità è già implicito nell'economia classica ed è
Cournot a tentarne per primo una formulazione rigorosa nel 1838. L'onore di aver reso popolare tale
importante concetto è tuttavia di Marshall che ne tratta nei suoi Principles (1890), anche se i primi
risultati in merito risalgono al 1885.
Definiamo elasticità della domanda di una merce rispetto al prezzo della stessa, il rapporto tra la
variazione relativa della quantità domandata e la variazione relativa del prezzo. In simboli:
εD =
∆q ∆p
∆q p
:
=
⋅
p
∆p q
q
dove ∆ denota una variazione finita piccola a piacere. Considerando variazione infinitesime e
richiamando alla mente la nozione di derivata, la formula dell'elasticità diventa:
ε
D
=
∂q p
⋅
∂p q
∂q
= lim
∆p→
∂p
dove
0
∆q
∆p
che esprime il rapporto tra la funzione marginale e la funzione media. Gli economisti considerano
l'elasticità in valore assoluto:
se ε D > 1
se ε D < 1
se ε D = 1
si ha domanda elastica;
si ha domanda inelastica;
si ha domanda unitaria.
Gli elementi fondamentali che determinano l'elasticità della domanda di un prodotto rispetto al
prezzo sono: l'esistenza di sostituti, la natura del bisogno che il prodotto soddisfa, il periodo di
tempo, il numero di usi cui il prodotto può essere destinato e infine la quota di reddito che viene
spesa per quel particolare prodotto.
2
Due osservazioni sono a questo punto opportune:
1) La difficoltà che sorge ogniqualvolta vengono mutate le unità di misura è qui assente, dal
momento che nella formula dell'elasticità entrano solo variazioni relative e perciò numeri puri (è
puro un numero privo di dimensione logica). L'elasticità, essendo il rapporto tra due numeri puri, è
anch'essa un numero puro.
2) L'elasticità della domanda rispetto al prezzo è un indice della reattività della quantità domandata
ad una variazione di prezzo. Quindi, i valori assunti dal coefficiente di elasticità vengono ordinati in
base ai valori assoluti e non ai valori algebrici.
Poiché la curva di domanda è decrescente, è evidente che se ∆p è maggiore di zero (il prezzo
aumenta) ∆q dovrà necessariamente essere negativo (la quantità domandata diminuisce). Quindi
l'elasticità della domanda rispetto al prezzo è sempre un numero negativo.
In generale, l'elasticità è diversa nei vari punti della curva di domanda ed è importante non
confondere il concetto di elasticità in un punto della curva con quello di pendenza nello stesso
punto.
5. ELASTICITÀ INCROCIATA DELLA DOMANDA
Come abbiamo già detto, la quantità domandata di una merce dipende anche dal prezzo di altre
merci. Per valutare quantitativamente l'influenza di variazioni del prezzo di un bene B sulla quantità
domandata di un altro bene A definiamo l'elasticità incrociata della domanda:
ε
A ,B
=
∆q A ∆pB
:
pB
qA
ovvero
ε A ,B =
∂q A pB
⋅
∂pB q A
Il valore assoluto ed il segno dell'elasticità incrociata rispecchiano la relazione che intercorre tra le
due merci. In generale avremo:
ε A,B > 0 se e solo se A e B sono beni succedanei
ε A,B = 0 se e solo se A e B sono beni indipendenti
ε A,B < 0 se e solo se A e B sono beni complementari
e quanto è maggiore il valore assoluto di ε A,B tanto più è intenso il legame, dell'un tipo o dell'altro,
esistente tra i due beni.
6. FUNZIONE DEL COSTO MARGINALE
Sia C=C(q) una funzione di costo totale. Per ogni q>0 sia possibile definire la derivata prima della
funzione C(q):
C ′( q ) =
∂ C( q )
∂q
Dal punto di vista economico, tale derivata esprime la variazione del costo totale che risulta da una
variazione infinitesima della quantità prodotta. La funzione derivata prima del costo totale è una
funzione C'(q):Ro+ →R che si chiama funzione del costo marginale. Il costo totale viene definito
come somma dei costi fissi e dei costi variabili:
3
C(q)= Cf + Cv(q)
segue che C'(q) = C'v(q) , cioè, il costo marginale totale è uguale al costo marginale variabile.
ESEMPIO: Sia la funzione del costo totale: C(q)=5q3-7q2+2q+17 dove Cf=17 e Cv(q)=5q37q2+2q.
La funzione del costo marginale è C'(q)=15q2-14q+2 mentre il costo medio Cm(q) è il rapporto tra
il costo totale e la quantità prodotta:
Cm(q)= C(q)/q = Cf /q + Cv(q)/q
In economia riveste particolare importanza la relazione tra la curva che rappresenta la funzione del
costo medio e quella che rappresenta la funzione del costo marginale.
Per q>0, si ha:
C'm(q)<0 quando C'(q)<Cm(q)
C'm(q)=0 quando C'(q)=Cm(q)
C'm(q)>0 quando C'(q)>Cm(q)
L'inclinazione della curva del costo medio sarà negativa, nulla o positiva, se la curva del costo
marginale sta, rispettivamente, sotto, incontri o sopra la curva del costo medio. Quindi, le curve del
costo marginale e del costo medio si intersecano nel punto minimo della curva del costo medio,
dove risulta C'(q)=0.
ESEMPIO: Se la funzione costo è data da C(q)=2q3-8q2+6q+36 si ha Cm(q)=2q2-8q+6+36/q e
C'(q)=6q2-16q+6.
Ora C'm(q)=4q-8-36/q2 e si osservi che C'(q)-Cm(q)= 6q2-16q+6-2q2+8q-6-36/q = 4q2-8q-36/q
a conferma numerica di quanto visto sopra.
7. RICAVO MARGINALE E RICAVO MEDIO
Per definire la funzione di ricavo totale si deve distinguere il caso di concorrenza perfetta (CP) in
cui si ha R(q)=pq dal caso in cui l'impresa abbia potere di mercato (concorrenza imperfetta,
monopolio: CI) in cui si ha R(q)=p(q)q. Se consideriamo il ricavo che l'impresa ha dalla vendita di
una unità di prodotto, si ottiene la funzione del ricavo medio, che è quindi dato, rispettivamente,
da:
R(q)/q = p
R(q)/q = p(q)
(in regime di concorrenza perfetta)
(in regime di concorrenza imperfetta o di monopolio)
Come si vede, il ricavo medio è uguale al prezzo di una unità di prodotto. In concorrenza perfetta,
quando il potere delle imprese di influire sul prezzo è nullo, il prezzo è un dato per l'impresa e la
funzione di ricavo medio è una costante. Quando invece l'impresa ha un certo potere di mercato,
essa sa che, normalmente, potrà vendere una maggiore quantità se applicherà un prezzo più basso.
Supponiamo che la funzione di ricavo totale sia derivabile e consideriamone la derivata prima, nel
caso di CP si ha R'(q)=p.
Tale derivata esprime la variazione del ricavo totale quando vi sia una variazione infinitesima della
quantità prodotta e venduta; è funzione della quantità prodotta e venduta e si chiama funzione del
ricavo marginale. Nel caso di CP, la funzione del ricavo marginale è una costante e coincide con
quella del ricavo medio. Nel caso di CI, si ha che R'(q)=p'(q)q+p dove naturalmente p'(q)<0 e
quindi R'(q)<p , cioè il ricavo marginale è minore del ricavo medio.
8. MASSIMIZZAZIONE DEL PROFITTO
4
Ogni impresa cerca di massimizzare il proprio profitto P determinato dalla differenza tra ricavi e
costi:
P(q)=R(q)-C(q) con p prezzo fisso. Da quanto abbiamo appreso dall'analisi matematica possiamo
dire che: condizione necessaria e sufficiente affinchè la funzione di profitto P(q) presenti un punto
di massimo è che:
1) La derivata prima della funzione profitto deve annullarsi nel punto di massimo;
2) La derivata seconda della funzione profitto calcolata nel punto di massimo deve essere minore di
zero.
Sviluppando in simboli la condizione 1) si ha che P'(q)=R'(q)-C'(q)=0 e quindi nel punto di
massimo il ricavo marginale deve essere uguale al costo marginale. Perchè sia verificata la
condizione 2) occorre che
R"(q)-C"(q)<0. In CP si ha R"(q)=0 e quindi la condizione 2) si
semplifica in C"(q)>0.
Anche il monopolista massimizza, nel breve periodo, i suoi profitti se R'=C' e R"<C" , dove
R(q)=p(q)q, cioè il prezzo non è costante ma dipende da q.
ESERCIZI DI RIEPILOGO
1) Data la funzione di domanda di una impresa: p=45-0.5q e la sua funzione del costo
medio Cm=q2-39.5q+120+125/q trovare il valore di q che massimizza il ricavo totale, che
minimizza i costi marginali, che massimizza il profitto. [45 ; 79/6 ; 25]
2) La funzione di domanda dell'acciaio è stata valutata in USA nel 1980, da p=250-50q (q in
migliaia di tonnellate e p in migliaia di dollari). Il costo medio dell'acciaio è pari a Cm=182/q + 50
(con Cm in migliaia di dollari). Determinare: le funzioni del costo totale, del costo marginale, del
ricavo totale, del ricavo marginale, del profitto. Quanto acciaio deve produrre l'impresa per avere il
profitto massimo e a quale prezzo?
[... ; q=2000 tonnellate con p=150 dollari per tonnellata]
5