Document

Fondamenti di Elettronica - Ingegneria Automatica - AA 2003/2004
2a prova in itinere- 5 febbraio 2004
Indicare chiaramente la domanda a cui si sta rispondendo. Ad esempio 1a) …
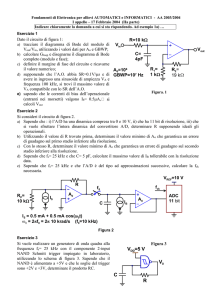
Esercizio 1
Vout(t)
Vin(t)
R2
Vin(t)
3V
-2µs
R1
R1=200kΩ
R2=800kΩ
C2=30pF
2 µs
6 µs
10µs
t
C2
a) Determinare il guadagno ideale dell’amplificatore mostrato in figura e disegnarne il diagramma di
Bode quotato del modulo e della fase.
b) Calcolare la resistenza di uscita in continua dell’amplificatore (dati operazionale: Ao=100 dB e
r0=1kΩ).
c) Si assuma per l’operazionale una risposta in frequenza ad anello aperto A(s)=Ao/(1+sτο) con Ao=100 dB,
τo=10 ms. Determinare il margine di fase dell’amplificatore.
d) Disegnare approssimativamente la risposta nel tempo al segnale di ingresso ad onda quadra Vin(t) mostrato
in figura quotandone il grafico sapendo che Vout(0)=0 V.
Esercizio 2
Si consideri il convertitore D/A a tre bit in figura. Quando un bit
vale 0 l’interruttore corrispondente è connesso alla massa.
a) Qual è l’interruttore corrispondente al bit più
significativo (MSB) e perché ? Quanto vale l’uscita Vo
quando viene connesso a – 2 V solo l’interruttore 4R
2R
corrispondente al bit meno significativo (LSB) ?
Bb
b) Che tensione di uscita corrisponde all’ingresso Bc=1 Ba
Bb=1 Ba=0 ?
c) Sapendo che l’operazionale ha Vos=50mV disegnare la
caratteristica statica di ingresso-uscita (si scelga a piacere il
segno dell’offset e si disegni la caratteristica corrispondente).
d) L’operazionale guadagna in continua A0= 105, e ha un solo R = 10 kΩ
polo a 10 Hz. All’istante t=0 tutti e tre i bit commutano da 0
a 1. Si scriva l’espressione della tensione di uscita Vo(t) in
funzione del tempo e se ne disegni un grafico quotato
(indicando cioè valori di tensione e costanti di tempo).
Esercizio 3
Si voglia caratterizzare sperimentalmente (NON mediante un simulatore!) la
risposta in frequenza di questo amplificatore invertente:
a) Elencare la strumentazione da utilizzare e disegnare (impiegando i
relativi simboli circuitali) il circuito con tutta la strumentazione connessa.
b) Descrivere in modo schematico i passi fondamentali della procedura
sperimentale impiegata (che cosa misuro? come lo misuro?) e come
vengono calcolati modulo e fase della FdT ad ogni frequenza.
R1=5 kΩ
R
VO
Bc
-2 V
R2
in
R1
Vdd
Vss
out
Fondamenti di Elettronica - Ingegneria Automatica - AA 2003/2004
2a prova in itinere- 5 febbraio 2004
Esercizio 1
a)
Il circuito a operazionale dato è retroazionato negativamente.
Nell'ipotesi che l'operazionale sia ideale, il guadagno |G |
dello stadio vale:
4
I D
-20dB/dec
R2
1
4
GID = −
=−
R1 1 + sR 2C 2
1 + sτ 2
dove:
τ 2 = R 2C 2 = 24µs
f2 =
1
2πτ 2
x
f =6631Hz
2
= 6631Hz
f
∠G
ID
180°
A lato è riportato il grafico di Bode risultante del
guadagno ideale.
90°
x
f =6631Hz
2
f
b)
Per calcolare la resistenza di uscita dell'amplificatore, inserisco la resistenza R0:
R2
R1
r
o u t
R0
Essendo il circuito retroazionato, calcolo la resistenza di uscita nel caso di amplificatore ideale
applicando un generatore di test di corrente.
R2
L'operazionale, che risulta retroazionato negativamente,
adatta la sua uscita per ottenere V+=V-, quindi si ottiene
R1
che V-=V+=0V.
It
Essendo
R0
Vt
R1
V − = Vt
= 0V
R1 + R 2
si ha necessariamente che Vt = 0V e, quindi:
Vt 0V
rout ID =
=
= 0Ω
It
It
La retroazione tenderà a ridurre la resistenza di
R2
uscita. Calcolo quindi la resistenza di uscita ad anello
aperto, che vale:
R1
Rout OPEN = R0 //( R1 + R 2) ≅ R0 = 1kΩ
con
Rout|OPEN
R 0 << ( R1 + R 2)
e il guadagno di anello, che vale:
R1
R1
200kΩ
GLOOP = − A0
≅ − A0
= −105
= −20000
R1 + R 2 + R0
R1 + R 2
1000kΩ
R0
Infine calcolo la resistenza di uscita ad anello chiuso:
Rout OPEN
1kΩ
rout =
=
≅ 50mΩ
1 − GLOOP 20001
c)
Per calcolare il margine di fase, calcolo il guadagno di anello dell'amplificatore:
A0
R1
1
GLOOP = −
dove Z 2 = R 2 //
1 + sτ 0 R1 + Z 2
sC 2
da cui, semplificando:
1 + sτ 2
R1
1
1 + sR 2C 2
= GLOOP (0)
GLOOP = − A0
(1 + sτ 0 )(1 + sτ p )
R1 + R 2 1 + sτ 0 1 + s ( R1 // R 2)C 2
dove
200kΩ
GLOOP (0) = −105
= −20000
1000kΩ
1
τ 0 = 10ms
con
f0 =
= 15.9 Hz
2πτ 0
1
τ 2 = R 2C 2 = 24 µs con
f2 =
= 6631Hz
2πτ 2
R1 // R 2 = 160kΩ
1
con
= 33.2kHz
fp =
τ p = ( R1 // R 2)C 2 = 4.8µs
2πτ p
Tracciando il grafico di bode si ottiene:
|GLOOP|
20000
G1 = GLOOP (0)
G1
fc = f p
x
f0=15.9Hz
o
f2=6631Hz
x
fp=33.2kHz
fc
f
fc
f
f0
= 48
f2
G1
= 1.59MHz
1
∠GLOOP
180°
90°
x
f0=15.9Hz
o
f2=6631Hz
x
fp=33.2kHz
Il margine di fase dell'amplificatore risulta pari a:
M = ∠GLOOP ( f c ) ≅ 90° essendo f c 10 volte maggiore delle singolarità presenti.
NOTA: il valore esatto del margine di fase vale:
f 
f 
f 
M = 180° − arctan c  + arctan 2  − arctan p  ≅ 90.96°
 f0 
 f0 
 f0 
d)
Il segnale applicato all'ingresso è una onda quadra di periodo T=8µs e di frequenza f=125kHz. La
risposta in frequenza di questo amplificatore, calcolata nel punto 1a, presenta un polo ad una frequenza
inferiore, pari a f 2 = 6631Hz < f . Posso, quindi, approssimare la risposta in frequenza ottenendo:
R2
R2 1
1
1
1
GID = −
≈−
=−
=−
R1 1 + sR 2C 2
R1 sR 2C 2
sR1C 2
sτ
che è la risposta in frequenza di un integratore. Perciò il segnale nel tempo in uscita all'amplificatore
sarà:
1
vout (t ) = − ∫ vin (t )dt dove τ = R1C 2 = 6µs
τ
si avrà, quindi:
dove:
da t=0s a t=t1 : vout (t ) = vout (0 ) −
3V
V
V
t = −0.5 t da cui vout (t1 ) = −0.5 2µs = −1V
µs
µs
6 µs
da t=t1 a t=t2 :
3V
V
vout (t ) = vout (t1 ) +
(t − t1 ) = 0.5 (t − t1 ) − 1V da
µs
6µs
V
cui vout (t2 ) = 0.5 4µs − 1V = 1V
µs
da t=t2 a t=t3 :
3V
V
vout (t ) = vout (t 2 ) −
(t − t2 ) = 1V − 0.5 (t − t 2 ) da
µs
6 µs
V
cui vout (t3 ) = 1V − 0.5 4 µs = −1V
µs
poi si ripete da t=t1
V
vin
3V
1V
vout
t
-1V
-3V
2µs
t1
6µs
t2
10µs
t3
R1
Esercizio 2
a)
I
Il DAC a tre bit proposto è sostanzialmente un
sommatore invertente a operazionale. Nell'ipotesi di
4R
2R
R
operazionale ideale, grazie alla condizione V+=VVo
posta dall'operazionale, la tensione in uscita al DAC
Ba
Bb
Bc
vale:
Vo = R 1 I
Vr
Vr
 da cui
 Vr
Vr=-2V
I = −
Ba +
Bb +
Bc 
4
2
R
R
R


R1
Vo = −
Vr 2 2 Bc + 21 Bb + 20 Ba = VLSB 2 2 Bc + 21 Bb + 20 Ba
4R
5kΩ
con VLSB = 2V
= 0.25V
40kΩ
Perciò il bit più significativo (MSB) risulta connesso a Bc, mentre il bit meno significativo risulta
(LSB) connesso a Ba.
La tensione in uscita per un ingresso pari a 1 (Bc=0 Bb=0 Ba=1) è pari a:
Vo(001b ) = VLSB ⋅1 = 0.25V
(
)
(
)
b)
Un ingresso binario pari a Bc=1 Bb=1 e Ba=0 corrisponde al numero 6, perciò la tensione in uscita
vale:
Vo(110b ) = VLSB ⋅ (4 + 2 + 0) = 0.25V ⋅ 6 = 1.5V
c)
Inserisco nel circuito i generatore equivalente della
tensione di offset Vos.
Per calcolare il suo effetto sulla tensione di uscita
bisogna analizzare tutti i possibili stati degli
interruttori. Tuttavia, in questo caso, gli interruttori
utilizzati sono dei deviatori che non scollegano mai
le resistenze R, 2R e 4R ma le commutano verso
massa o verso Vr.
R1
I
4R
2R
R
Vos
Ba
Bb
Vo
Bc
Vr=-2V
Applico la sovrapposizione degli effetti per calcolare il contributo di Vos sull'uscita:
R1
I
4R
2R
R
Vos
Ba
Bb
Vo|Vos
Bc
si ottiene un circuito che non dipende dalla posizione degli interruttori, quindi:

R1 
Vo Vos = Vos1 +
= 1.875Vos = 0.094V = 0.375LSB
 R 
EQ 

−1
REQ
4
 1 1
= R // 2 R // 4 R = 1 + +  R = R = 5.71kΩ
7
 2 4
La tensione complessiva in uscita vale: Vo
1.84V
Vo = 0.25V ⋅ n + 0.094V
1.59V
1.34V
1.09V
0.84V
0.59V
0.34V
0.09V
Vo|Vos
Caratteristica ideale
Vo=VLSB n
0 1 2 3 4 5 6 7
n
d)
Commutare tutti gli interruttori da 0 a 1 vuol dire far commutare l'uscita dal valore
Vo(000b ) = 0V
al valore
Vo(111b ) = 1.5V
In pratica, commutare è equivalente a considerare il DAC un amplificatore invertente (mostrato in
figura)
R1
I
4R
2R
R
Vo
Vin
0V
-2V
al cui ingresso viene applicato un gradino di ampiezza Vr.La sua risposta a tale gradino sarà la risposta
del DAC alla commutazione degli interruttori. Calcolo, quindi, la banda di questo amplificatore:
-) guadagno ideale:
R1
5kΩ
GID = −
=−
= −0.875
REQ
5.71kΩ
-) guadagno d'anello
1
τ0 =
= 15.9ms
REQ
A0
2πf 0
GLOOP = −
dove
1 + sτ 0 REQ + R1
f 0 = 10 Hz
-) guadagno di andata
|G|
GANDATA
A0
R1
46667
41667
G ANDATA = GIDGLOOP =
=
1 + sτ 0 REQ + R1 1 + sτ 0
A0 = 105
Il circuito presenta, quindi, un solo polo ad anello
chiuso alla frequenza di:
41667
f H = f0
= 533kHz
0.875
1
τH =
= 298ns
2πf H
Perciò la risposta del DAC alla commutazione degli
ingressi sarà del tipo esponenziale di funzione:
t
t
−


−


τH 

= 1.75V 1 − e 298 ns 
Vo(t ) = Vr ⋅ GID 1 − e






Esercizio 3:
a)
Elenco della strumentazione necessaria:
• 2 Alimentatori DC per la polarizzazione
dell'operazionale (+Vcc e -Vcc)
• un generatore di forme d'onda sinusoidale
• un oscilloscopio a due canali
da collegare secondo il seguente schema
GID
0.875
GREALE
x
f0=10Hz
f
fH
Vo
1.75V
0V
t
298ns
R2
+Vcc
R1
Generatore
sinusoidale
-Vcc
+
+
Oscilloscopio
Oscilloscopio
b)
- canale 2
- canale 1
Per misurare la risposta in frequenza
dell'amplificatore in esame occorre alimentare il
circuito e applicare in ingresso un segnale sinusoidale tramite un generatore sinusoidale a frequenza e
ampiezza variabile.
∆Vout
∆Vin
Con l'oscilloscopio misurare sia il segnale in ingresso al circuito (canale 2) sia il segnale in uscita al
circuito (canale 1).
La misura avverrà per punti misurando il valore del guadagno e della fase per diversi valori di
frequenza.
Per ciascun valore di frequenza è necessario:
-) regolare l'ampiezza del segnale in ingresso per consentire una corretta misura del guadagno e della
fase senza incorrere in non-linearità dell'amplificatore (es. slew-rate, saturazione dell'uscita).
-) sull'oscilloscopio misuro l'ampiezza picco-picco del
V
vin
segnale di ingresso (∆Vin) e del segnale in uscita
(∆Vout), come mostrato in figura.
vout
il guadagno dell'amplificatore risulta pari a:
G=∆Vout/∆Vin
t
-) sempre sull'oscilloscopio misuro il periodo della
sinusoide applicata T, e il ritardo rispetto ad essa della
sinusoide misurata in uscita al circuito (dT). Lo
dT
sfasamento introdotto dall'amplificatore risulta pari a:
ϕ=360°⋅dT/T
T
Se non indicata dal generatore sinusoidale, ottengo la
frequenza della sinusoide applicata con:
f=1/T
Eseguo la misura di guadagno e fase a diverse frequenze per coprire la banda di interesse
dell'amplificatore, compilando la seguente tabella che sintetizza i risultati della misura
frequenza | ∆Vin | ∆Vout | T | dT | G | ϕ