Esercizi di Analisi 1 - Alberto Valli - AA 2015/2016 - Foglio 5
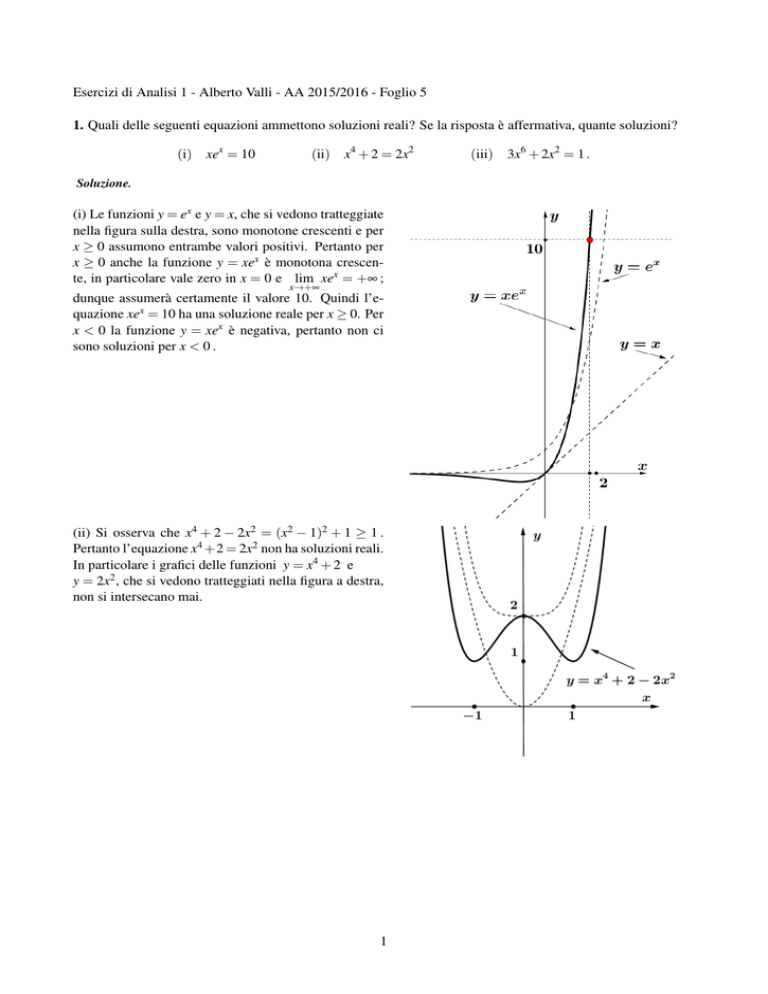
1. Quali delle seguenti equazioni ammettono soluzioni reali? Se la risposta è affermativa, quante soluzioni?
(i) xex = 10
(ii) x4 + 2 = 2x2
Soluzione.
(i) Le funzioni y = ex e y = x, che si vedono tratteggiate
nella figura sulla destra, sono monotone crescenti e per
x ≥ 0 assumono entrambe valori positivi. Pertanto per
x ≥ 0 anche la funzione y = xex è monotona crescente, in particolare vale zero in x = 0 e lim xex = +∞ ;
x→+∞
dunque assumerà certamente il valore 10. Quindi l’equazione xex = 10 ha una soluzione reale per x ≥ 0. Per
x < 0 la funzione y = xex è negativa, pertanto non ci
sono soluzioni per x < 0 .
(ii) Si osserva che x4 + 2 − 2x2 = (x2 − 1)2 + 1 ≥ 1 .
Pertanto l’equazione x4 +2 = 2x2 non ha soluzioni reali.
In particolare i grafici delle funzioni y = x4 + 2 e
y = 2x2 , che si vedono tratteggiati nella figura a destra,
non si intersecano mai.
1
(iii) 3x6 + 2x2 = 1 .
(iii) Le funzioni y = 3x6 e y = 2x2 , che si vedono tratteggiate nella figura sulla destra, sono monotone crescenti
per x ≥ 0 dunque anche la loro somma, cioè la funzione y = 3x6 + 2x2 , è monotona crescente per x ≥ 0 .
Inoltre, in modo analogo a quanto osservato nel caso
(i), la funzione y = 3x6 + 2x2 vale zero per x = 0 e
lim 3x6 + 2x2 = +∞ ; dunque assumerà certamente il
x→+∞
valore 1. Quindi l’equazione 3x6 + 2x2 = 1 ha una soluzione reale per x ≥ 0. Dal momento che y = 3x6 + 2x2
è simmetrica rispetto all’asse y, si conclude che l’equazione 3x6 + 2x2 = 1 ha una soluzione reale anche per
x ≤ 0. Le soluzioni sono distinte e sono evidenziate nel
disegno sulla destra.
2
2. Sia f : R → R una funzione continua tale che
x2
≤ f (x) ≤ 2x2
2
∀ x ∈ [0, 1].
Quali delle seguenti affermazioni sono vere per qualsiasi funzione f che soddisfi quanto sopra indicato?
(i) esiste x0 ∈ [0, 1] tale che f (x0 ) =
7
4
3
2
f (x0 ) = 12
(ii) esiste x0 ∈ [0, 1] tale che f (x0 ) =
(iii) esiste x0 ∈ [0, 1] tale che f (x0 ) = 1
(iv) esiste x0 ∈ [0, 1] tale che
.
2
Soluzione. Nella figura sotto sono rappresentati i grafici delle funzioni y = x2 e y = 2x2 .
Si osserva che la funzione f deve assumere agli estremi dell’intervallo [0, 1] i seguenti valori
f (0) = 0
1
≤ f (1) ≤ 2
2
e
Inoltre, per la continuità di f , possiamo applicare il teorema degli zeri nell’intervallo [0, 1] e concludere che
necessariamente la funzione f assumerà il valore 12 per qualche x0 ∈ [0, 1] . Pertanto la risposta corretta è
l’opzione (iv) .
x2
Un’altra modalità di risoluzione poteva esser quella di notare che la funzione f (x) =
soddisfa le richieste
2
del quesito e l’opzione (iv) è l’unica affermazione corretta.
3
3. Quali delle seguenti funzioni non sono derivabili nel punto x = 0?
(i) |x| sin x
(ii) |x sin x|
(iii) x | cos x|
(iv) |x| cos x .
Soluzione. È noto dalla teoria che una funzione f : R → R è derivabile in un punto x0 ∈ R se esiste ed è finito
il limite
lim
x→x0
f (x) − f (x0 )
x − x0
|x| sin x 1
= 0 , dunque la funzione y = |x| sin x è derivabile in x = 0 .
x→0
x
|x sin x|
(ii) lim
= 0 , dunque la funzione y = |x sin x| è derivabile in x = 0 .
x→0
x
x| cos x|
(iii) lim
= 1 , dunque la funzione y = x| cos x| è derivabile in x = 0 .
x→0
x
|x| cos x
|x|
(iv) lim
= lim
che non esiste. Pertanto la funzione y = |x| cos x non è derivabile in x = 0 .
x→0
x→0 x
x
Nella figura sotto riportiamo i grafici delle funzioni prese in esame.
(i) lim
1
Si ricordi il limite notevole lim
x→0
sin x
=1
x
4
5. Considerate la funzione k(x) = (x − 1)(x2 + 2x − 3).
(i) Tracciatene a grandi linee il grafico.
(ii) Provate che l’equazione e3x + e2x − 5ex + 3 = 0 ammette una sola soluzione, e determinatela .
Soluzione.
(i)
(ii) Si noti che k(x) = (x − 1)(x2 + 2x − 3) = (x − 1)(x − 1)(x + 3) = (x − 1)2 (x + 3) , inoltre
k(ex ) = e3x + e2x − 5ex + 3 , pertanto
e3x + e2x − 5ex + 3 = 0
⇐⇒
k(ex ) = 0
5
⇐⇒
ex = 1
⇐⇒
x=0
6. Dite quali delle seguenti funzioni g sono invertibili, ed, in caso affermativo, determinate la funzione inversa.
(i) g(x) = log(x +
p
x2 + 1) , x ∈ R
(ii) g(x) =
ex + e−x
, x ≥ 0.
2
Soluzione.
(i) Per prima cosa verifichiamo che la funzione g è definita per ogni x ∈ R. Infatti si ha
p
√
x2 + 1 > x2 = |x| ≥ −x ∀ x ∈ R ,
√
dunque x + x2 + 1 > 0 per ogni x ∈ R. Veniamo al calcolo della derivata: si ha
1
x
1
√
g0 (x) =
1+ √
=√
> 0 ∀ x ∈ R,
x + x2 + 1
x2 + 1
x2 + 1
dunque g è strettamente crescente in R e quindi invertibile.
Determiniamo la funzione inversa di g.
√
p
2
y = log(x + x2 + 1) ⇐⇒ ey = elog(x+ x +1)
⇐⇒
ey = x +
p
x2 + 1
⇐⇒
e2y − 2xey − 1 = 0
ey − e−y
=x
2
ex − e−x
Pertanto la funzione inversa di g sarà definita da g−1 (x) =
.
2
Nella figura sotto si vedono rappresentati il grafico di g (tratteggiato) e il grafico di g−1 .
e2y − 1
= 2x
ey
⇐⇒
(ii) Si osserva che g(x) =
x ≥ 0.
⇐⇒
ex + e−x
= cosh(x) ed è strettamente crescente per x ≥ 0, quindi g è invertibile per
2
Determiniamo la funzione inversa g−1 .
p
4y2 − 4
⇐⇒ 2y = e (e + 1) ⇐⇒ e − 2ye + 1 = 0 ⇐⇒ e =
2
p
p
p
⇐⇒ ex = y + y2 − 1 ⇐⇒ log(ex ) = log(y + y2 − 1) ⇐⇒ x = log(y + y2 − 1)
√
Dunque la funzione inversa g−1 (x) = log(x + x2 − 1) .
ex + e−x
y=
2
−x
2x
2x
x
x
Nella figura sotto sono riportati il grafico della funzione g (tratteggiato) e il grafico di g−1 .
6
2y +
8. Sia f una funzione derivabile in [0, 1]. Quali delle seguenti situazioni sono possibili?
(i) f 0 (x) < 2 ∀ x ∈ [0, 1] , f (0) = −1 , f (1) = 1
(ii) f 0 (x) >
1
1
1
∀ x ∈ [0, 1] , f (0) = − , f (1) = .
2
2
2
Soluzione.
(i) Essendo la funzione derivabile, per il teorema del valor medio di Lagrange, deve esistere t ∈ ]0, 1[ tale che
f (1) − f (0)
f 0 (t) =
= 2 . Pertanto non vi è nessuna funzione derivabile in [0, 1] con f (0) = −1 e f (1) = 1 tale
1−0
che la condizione f 0 (t) < 2 ∀ x ∈ [0, 1] sia verificata.
1
(ii) Si vede subito che la funzione f (x) = x − , il cui
2
grafico è rappresentato in figura, verifica le condizioni
richieste; pertanto la situazione in (ii) è possibile.
7