NOME:……………………………………… COGNOME:…………………………………………
CLASSE:…………………………………………
DATA:………………………..
VERIFICA DI TRIGONOMETRIA
Esercizi dall’esame
1. L’espressione cos 2 5 sin 2 5 è equivalente a
⃝1
⃝2
⃝ cos 2 sin 2 5
⃝ cos 2 10
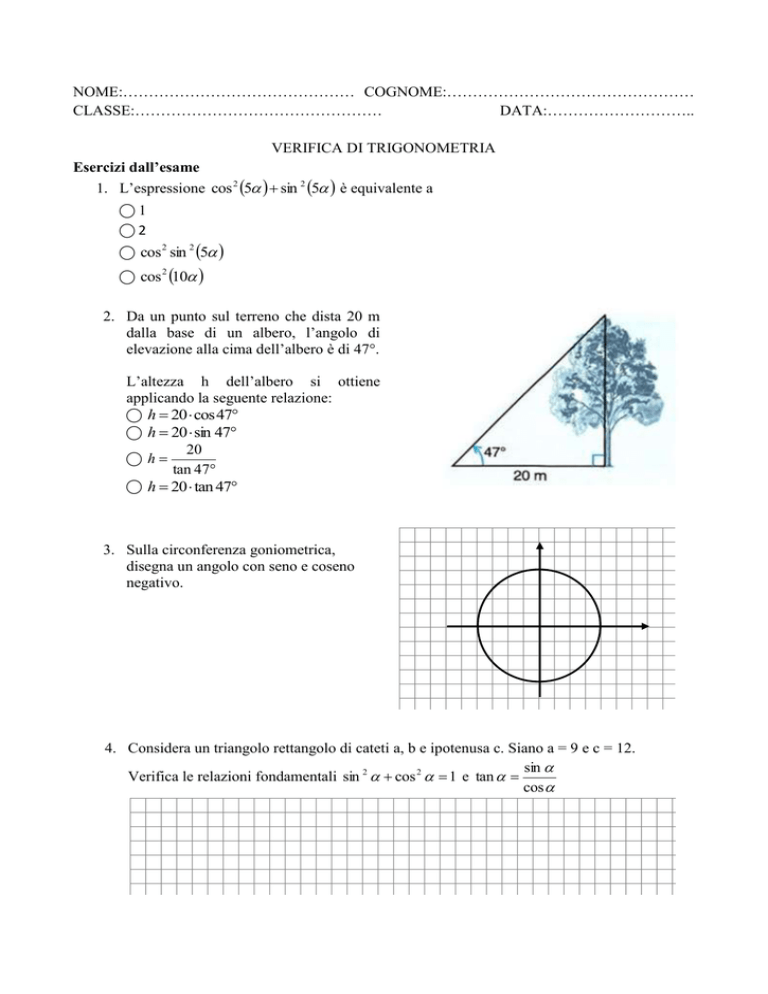
2. Da un punto sul terreno che dista 20 m
dalla base di un albero, l’angolo di
elevazione alla cima dell’albero è di 47°.
L’altezza h dell’albero si ottiene
applicando la seguente relazione:
⃝ h 20 cos 47
⃝ h 20 sin 47
20
⃝ h
tan 47
⃝ h 20 tan 47
3. Sulla circonferenza goniometrica,
disegna un angolo con seno e coseno
negativo.
4. Considera un triangolo rettangolo di cateti a, b e ipotenusa c. Siano a = 9 e c = 12.
sin
Verifica le relazioni fondamentali sin 2 cos 2 1 e tan
cos
Problemi
5. Un palazzo proietta un’ombra di 64 metri in un momento in cui i raggi solari formano con il
suolo un angolo di 50°. Quanto è alto il palazzo?
6. Una scala a pioli è appoggiata alla facciata di un palazzo. Forma con il suolo un angolo di
74° e il punto d’appoggio dista 1,4 m dalla parete della casa. Quanto è lunga la scala?
7. Un asse lungo 25 cm è appoggiato a una parete e forma con il pavimento un angolo di 61°.
Determina l’altezza a cui arriva l’asse sulla parete.
8. La base della Piramide di Cheope misura 230 m ed è alta 147,2 m. Qual è l’angolo di
pendenza di una delle sue facciate laterali? (Attenzione: la sezione di una piramide è un
triangolo isoscele).
9. Un aereo sta sorvolando su Milano all’altezza di 1520 metri. Deve atterrare a Roma, che
dista da Milano 400 km (fai l’equivalenza). Quale sarà l’angolo di depressione che dovrà
tenere l’aereo per atterrare a Roma? Quanti chilometri dovrà percorrere in aria?
10. Sulla parete di un grattacielo c’è una vetrata davvero molto alta. Un geometra in pensione,
incuriosito, si posiziona di fronte all’edificio, a una distanza di 50 metri dalla facciata, e
constata che la base della vetrata e la sua sommità vengono viste, da lì, secondo angoli di
elevazione di 23° e di 52° rispettivamente. Quanto misura la vetrata?












