PROBLEMI GENERALI
Applicazione n° 1
DI RELATIVITA’ (DINAMICA (URTI) ED ONDE)
(Conservazione energia e Momento)
Una particella di massa 2.00 MeV/c2ed energia cinetica 3 MeV collide con una particella stazionaria di
massa 4 MeV/c2. Dopo la collisione le 2 particelle rimangono attaccate. Trovare:
1)
Il modulo del momento iniziale. 2) la velocità finale del sistema a 2 particelle. 3) la massa del
sistema a 2 particelle.
Soluzione
1) Il momento iniziale del sistema è il momento iniziale della particella in moto incidente. Il
momento di una particella è legato alla sua energia ed alla sua massa : E12 =p12+ m12c4. Quindi
p1c = √E12- m12c4. Quindi il momento iniziale è dato da: p1∙c= √52- 22 = √21 = 4,58 MeV/c.
2) Data uf la velocità finale del sistema a2 particelle, abbiamo: (uf/c) = pi∙c/E. Per la conservazione
dell’ energia totale l’ energia finale vè uguale a quella iniziale. Quindi E1TOT = E1M + E1CIN =
2+3 =5 MeV. Quindi l’ energia totale finale del sistema è : Ef = E1 + E2 = (5+4) = 9 MeV. Per la
conservazione del momento, il momento finale del sistema è uguale al momento iniziale :
pf = pi = 4,58 MeV/c. Calcoliamo la velocità del sistema a due particelle a partire dalla sua
energia totale e del momento usando: E∙ui = pc2. Quindi (pc/E) = (ui/c) Quindi ui/c = 4,58/9 =
0,509c.
3) Si trova la massa finale con l’ equazione di Einstein relativa al sistema a due particelle.
Abbiamo: E2 = (pc)2+ (m0c2)2. Tenendo conto dei valori: abbiamo: 92 = (4,58)2+ (Mf)2 . Quindi
abbiamo: Mf = 7,75 MeV/c2.
Applicazione n° 2 (Energia cinetica nell’ urto)
Si osservi che la massa del sistema aumenta da 6,00 MeV/c2 a 7,75 MeV/c2. Questo aumento di massa,
moltiplicato per c2, è uguale alla perdita di energia cinetica del sistema. Dobbiamo fare:
1) Trovare l’ energia cinetica finale del sistema a 2 particelle.
2) Trovare la perdita di energia cinetica ECINP nella collisione.
3) Mostrare che Ecinp = (ΔM/c2) dove ΔM è la variazione di massa del sistema.
Soluzione
1) L’ energia totale del sistema è 9 MeV. L’ Energia di Massa del sistema a 2 particelle è 7,75 MeV.
Quindi l’ energia cinetica del sistema: ECINS = ETOT – EMASSA = 9 – 7,75 = 1,25 MeV.
2) L’ energia cinetica iniziale Ecini della particella 1 in moto è 3 MeV. L’ energia cinetica finale del
sistema a 2 particelle è 1,25 MeV. Quindi ΔECIN = ECINF- ECININ = 1,25 – 3 = - 1,75 MeV.
3) L’ energia di massa iniziale è : EM1+ EM2 è : 2+4 = 6 MeV/c2. La energia di massa finale è: 7,75
MeV/c2. Quindi la variazione di Energia di massa è : ΔEMTOT = 7,75- 6 = 1,75 MeV.
Applicazione n°3 (Conservazione della quantità di moto relativistica)
Un satellite inizialmente in quiete nello spazio profondo esplode in due pezzi. Uno ha massa di 150 Kge e
si muove dal punto in cui è avvenuta l’ esplosione con una velocità di 0,76c. L’ altro pezzo si muove in
direzione opposta con una velocità di 0,88 c. Trovare la massa del secondo pezzo di satellite.
Soluzione
L’ idea di base nello studio di questo sistema è che , poiché sul satellite non agiscono forze esterne , la
quantità di moto del sistema si conserva. La quantità di moto iniziale è zero, quindi la quantità di moto
finale è anch’ essa zero. Quindi abbiamo pTOTIN = pTOTFIN = 0. Abbiamo : p1FIN + p2FIN =0. Quindi: p2FIN = p1FIN.
Calcoliamo il modulo della prima quantità di moto p1 con la formula della dinamica: p = m1ϒv ; quindi: p1 =
(m1∙v1 )/√(1-v12/c2 = (150∙0,76∙(3∙108) /√(1-(0,76c)2/c2 = (3,42∙1010/0,65 = 5,3∙ 1010 Kgm/s. Uguagliamo la 2°
quantità di moto alla 1° quantità di moto: p2 = (m2∙v2/(√(1-v22/c2) = p1. Ricaviamo la massa m2 dalla formula
inversa : m2 = (p1/v2)/√(1-v22/c2). Eseguendo il calcolo si ottiene m2 = 95 Kg.
Oss. : Un modo conveniente di pensare alla quantità di moto data dall’ equazione p = (m∙v)/(√(1-v2/c2) è
considerare una massa che aumenta con la velocità. L’ espressione classica della quantità di moto p viene
ottenuta da quella relativistica nell’ approssimazione v << c : p = mv (1+(1/2v2/c2+…) = mv.
Applicazione n° 4 (Quantità di moto in urto anelastico)
Un giocatore di football americano, che pesa 88 Kg e ha una velocità di 2 m/s , urta frotalmente con
giocatore della squadra avversaria che pesa 120 Kg. Dopo la collisione i giocatori rimangono attaccati l’
uno all’ altro fermandosi. Trova la velocità del giocatore della squadra avversaria, assumendo che la
velocità della luce sia 3 m/s.
Soluzione
La velocità del 2° giocatore è data dalla legge della conservazione della quantità di moto. Quindi
abbiamo: pR1I + pR2I = pF1+2 = 0. Calcoliamo la quantità di moto della 1° particella : pR1I =
(m1∙ v1)/√(1-v12/c2). Quindi pR1I = (88∙2)/(√(1-4/9) = (176∙3)/√5 = 236,13 Kg m/s. Abbiamo che pR2I = pR1I. La
formula quindi dà : pR1I = m2∙v2∙/√(1-v22/c2) . Quindi abbiamo v2 ricavato dalla formula inversa v2 = 1,6 m/s.
ENERGIA NELLA DINAMICA RELATIVISTICA
Consideriamo, per esempio, un corpo che ha massa m0 quando è in quiete. Einstein dimostrò che, quando
il corpo è in movimento con velocità v, la sua energia totale,E, è data dalla seguente espressione:
E = m0∙c2/(√(1-v2/c2) = m∙c2 .
Questo è la formula di Einstein della equivalenza energia- massa. Quindi abbiamo la formula nel caso
classico:
E = m0∙c2(1+1/2 v2/c2 +…) = m0c2+ 1/2mv2+….
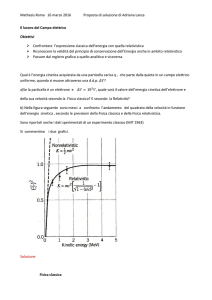
Applicazione n° 5 ( Energia cinetica delle particelle)
Calcolo dell’ energia necessaria per accelerare : a) un elettrone; b) un protone sino ad una velocità pari
alla metà di quella della luce. In entrambi essi, confrontare i valori relativistici, con quelli newtoniani.
Soluzione
Quando v = 0,5 c, abbiamo che ϒ = 1/(1-v2/c2)1/2 . Calcoliamo il valore = 1,1547. Allora ECIN =m0∙∙c2∙(ϒ-1) =
0,1547 m0∙c2.
Per il valore non relativistico : ECIN = 1/2∙m∙v2 = mc2 (1/2∙ v2/c2) = 0,125 mc2. Allora : ECIN(rel)/E(New.)=
1,2376. Per cui ECIN(REL. ) è circa il 24% più elevata dell’ energia cinetica ECIN (New.).
Osserviamo che questo rapporto è indipendente dalla massa della particella. I valori dell’ Energia
cinetica per l’ elettrone ed il protone sono rispettivamente: elettrone ECIN (rel.) = 0,075 MeV e protone ha
energia cinetica ECIN rel.) = 145,155 MeV. Ciò dimostra che l’ energia necessaria per accelerare un
protone ad una certa velocità è circa 2000 volte maggiore di quella necessaria per accelerare un
elettrone.
Applicazione n° 6 ( Energia di una particella)
Supponi che un neutrone viaggi alla velocità di 0,99 c. Calcola :
1) La sua energia totale.
2) La sua energia a riposo.
3) La sua energia cinetica.
Soluzione
1) L’ Energia a riposo del neutrone è 939,60 MeV/c2. Quindi l’ energia a riposo data in Joule è con il
fattore di conversione 1,6∙10-19 , e quindi abbiamo il valore di 0,15 nJ.
2) L’ Energia totale della particella neutrone è data da ETOT = m0∙ϒ∙c2 = 939,600141 = 6660,65 MeV/c2.
Quindi in Joule abbiamo il valore di 1,1 nJ.
3) L’ Energia cinetica è data da : ECIN = (ETOT – EMASSA) = 5721 MeV /c2 = 0,92 nJ.
Applicazione n° 7
(Differenza di massa in una trasformazione macroscopica)
Supponi di comprimere di 38,0 cm una molla avente una costante elastica di 544 N/m . Calcola l’ aumento
della massa della molla
Soluzione
La lunghezza di accorciamento Δx = 38,0 cm =0,38 m con costante K = 544 N/m . L’Energia accumulata è
data dalla formula : EACC = 1/2∙K∙Δx2 = 0,5∙544∙(0,38)2 = 39,28 J. In presenza di tale Energia macroscopica
abbiamo Δm = (E/c2) = (39,28/(3∙108)= 4,3∙ 10-16 Kg. ( aumento di massa piccolissimo).
Applicazione n° 8 (Energia dinamica per creare Energia di massa)
Determinare l’ energia necessaria per creare una coppia elettrone – positrone in interazione fotonica.
Soluzione
Per creare una coppia elettrone- antielettrone di Massa (0,511∙2) = 1,022 MeV/c2 che necessitano di una
energia pari a questa massa cioè 1,022 MeV. Quindi l’ energia sviluppata è, data in Joule, la seguente:
(1,022 ∙ 106∙∙ 1,6∙10-19) = 1,6∙ 10-13J.
Applicazione n° 9 (Energia per creare energia elettromagnetica)
When a proton encounters an antiproton, the two particles annihilate each other, producing two gamma
rays. Assuming the particles were at rest when they annihilated, find the energy of each of the two gamma
rays produced.
Soluzione
Quando I 2 protoni si annichilano in quiete, la loro energia complessiva è data da : 2∙ ENPROT = 2∙ 938,82 =
1877,64 MeV Per esprimere l’ energia in unità S.I. 1877,64 ∙ 1,6 ∙ 10-19 = 3,1 ∙ 10-10 J. Quindi ogni raggio
gamma ha energia (3,1∙ 10-10 /2 = 1,51 nJ.
Applicazione n° 10
(Calcolo velocità da energia cinetica)
Un razzo con massa di 2,7 ∙ 106 Kg ha un’ energia cinetica relativistica di 2,7 ∙ 1023 J. A quale velocità
viaggia il razzo?
Soluzione
L’ energia cinetica è dalla formula: ECIN = (ϒ-1)∙m0∙c2 ; quindi (1/√(1-v2/c2) – 1) ∙m0∙c2 = 2,7∙ 1023 J L’ Energia
di massa è data da EMASSA = 2,7∙ 106∙9∙ 1018 = 2,43∙1025 J. L’ energia totale è data da : 2,43∙1025+ 2,7∙1023 =
2,457∙ 1025 J. Da cui abbiamo l’ equazione: 2,43∙ 1025 = 2,457∙(1-√v2/c2) ; (1-v2/c2) = 0,894. E quindi : (v2/c2)
= 0,894. Quindi v = 0,32 c.
Applicazione n° 11 (Energia – massa per il Sole)
Il Sole irraggia energia ad un ritmo di 3,92 ∙ 1026 W. Calcola la corrispondente diminuzione della
massa del Sole in ogni secondo di irraggiamento.
Soluzione
Se l’ Energia irraggiata dsal Sole in 1,00 s è ΔE , la corrispondente variazione di massa è data da :
m= ΔE/c2. Per trovare E, ricordiamo che la potenza è l’ energia nell’ unità di tempo è P = E/Δt perciò l’
energia irraggiata dal sole in 2 secondi è : E = P∙Δt = 3,92∙ 10 26 W∙ 1 s = 3,92∙ 1026 J. Dividiamo l’ energia
per il quadrato della velocità della luce,c2, . Quindi m =E/c2= (3,92∙ 1026 J/9∙ 1016 = 4,36∙ 109 Kg.
Applicazione n° 12 ( Evoluzione di una stella)
Soluzione
L’ Energia emessa ,sviluppata in una diminuzione di massa è data da: E = (7,36∙ 1022)∙9∙1016 =
6,62∙ 1039J. La Potenza emessa in mezzo milione di anni (0,5∙ 106 anni) . La Potenza emessa in mezzo
milione di anni è P = 0,5 ∙ 106∙86400∙365 = 1,58∙ 1013 secondi.. La Potenza data : E/c = (6,6224∙ 1029/1,58∙
1013) = 4,19∙ 1017 W = 4,19∙ 1017 W = 4,19∙ 10∙108 GW.
Applicazione n° 13 (Perdita di massa del Sole)
La costante solare Cs = 1,4 KW/m2 esprime la quantità di energia che dal Sole arriva sulla terra nell’ unità
di tempo e di superficie. Questa energia è irradiata allo stesso modo in tutte direzioni. Calcolare la
quantità di massa perduta dal Sole in un giorno.
Soluzione
La potenza emessa è 1400 W/m2n . La superficie interessata è S = 4∙π∙R2 = 4∙π∙(1,5∙1011)2
Applicazione n° 6
(Cinematica del moto relativistico)
Nel sistema di riferimento S un raggio di luce si sposta nel verso delle x positive ed un altro si muove nel
verso opposto. Qual è la velocità del primo raggio di luce visto nel sistema di riferimento solidale con il
secondo? Risolvi il problema prima nell’ ambito della meccanica classica e poi in quello della meccanica
relativistica.
Soluzione
Risolviamo ilo problema ponendo u =c ( la velocità del raggio di luce rispetto a S è c) e v = -c ( il sistema di
riferimento S’ solidale con il secondo raggio di luce si muove nel verso negativo delle x con una velocità di
modulo c). Nell’ ambito della meccanica classica otteniamo: u’ = u-v = c-(-c) = 2c. Il primo raggio di luce si
allontana dal secondo con una velocità doppia di quella che esso ha nel sistema S. Secondo la teoria della
relatività, invece, la velocità relativa u’ è; vedremo che queste ultime prevedono una legge di
composizione della velocità diversa, data dalla formula: u’ =( u-v)/(1-uv/c2) e u’ = (c-(-c))/1-c∙(-c)/c2 =(2∙c)/2
= c. Il risultato ottenuto mostra che, anche vista da un altro raggio luminoso, la velocità della luce rimane
uguale a c.
Applicazione n° 7 ( Composizione di velocità relativistica)
Una particella si muove verso destra nel sistema S con velocità u = (2/3)∙ c mentre il sistema S’ si muove,
rispetto a S, verso destra con velocità v = c/3. Qual è la velocità della particella in S’?
Soluzione
La velocità della particella nel sistema di riferoimento S’ è data dalla formula di bcomposizione delle
velocità : u’ = (u-v)/(1-(u∙v)/c2 =( (2/3)∙c – (c/3))/(1-(2/3∙c)(1/3∙c) = (1/3)c/(1-(2/9(c2/c2) = (c/3)∙(9/7) = 3/7c.
Applicazione n° 8 ( Studio cinematico reazione chimica)
Un materiale radioattivo in quiete emette due particelle nella stessa direzione ma in verso opposto. La
velocità di ognuna delle due particelle, misurata in laboratorio, ha un modello pari all’ 80% della velocità
della luce. Calcola:
a) La velocità della prima particella nel sistema di riferimento della seconda nell’ ambito della teoria
relativistica.
b) La velocità della prima particella nel sistema di riferimento della seconda nell’ ambito della
meccanica classica.
Soluzione
a) La composizione delle velocità delle due particelle è data dalla legge di composizione di
Galileo: u’ = u+ v = 0,8∙c+ 0,8∙c = 1,6∙c.
b) Con la legge di composizione delle velocità relativistica: u’ = (u-v)/(1-u∙v/c2) =
(0,8∙c+0,8∙c)(1+0,64∙c2/c2) =(1,6∙c)/1,64 = 0,98c.
Applicazione n° 9 ( Viaggio astronave nella relatività)
Soluzione
La velocità del proiettile rispetto al sisatema in movimento è: u’ = (3/4)∙c- (1/4)∙c = (1/2)∙c. La velocità del
proiettile secondo le leggi della relatività : u’ = (0,5)∙c(1-(3/16)c2/c2 = (0,5∙c)/(13/16) = 8/13 ∙c.