Moto Circolare Uniforme
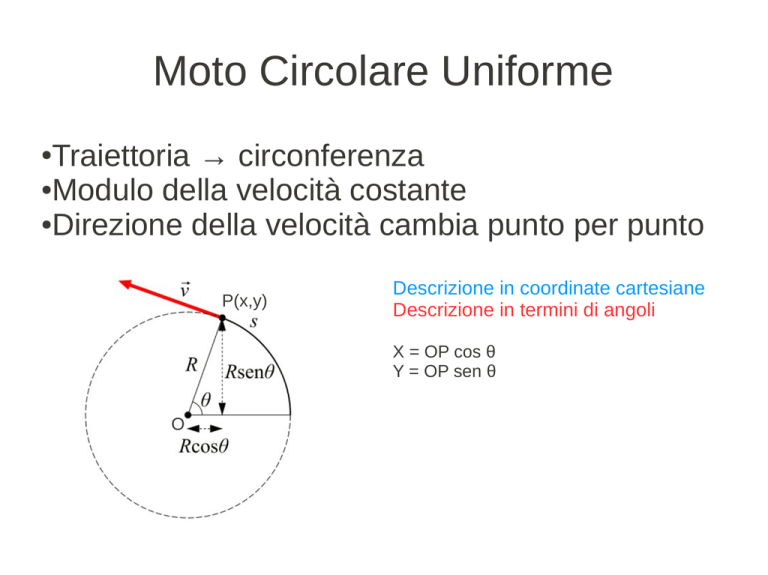
Traiettoria → circonferenza
●Modulo della velocità costante
●Direzione della velocità cambia punto per punto
●
P(x,y)
Descrizione in coordinate cartesiane
Descrizione in termini di angoli
X = OP cos θ
Y = OP sen θ
O
P(x,y)
Velocità tangenziale
2πR= v T
v=2πR/T
velocità angolare
s→θ
v→ω
O
ω= θ /T
θ=2π
ω= 2π/T
v = ωR
Modulo velocità costante ma non direzione....
a=at+ac
Variazione direzione velocità nel tempo
Variazione modulo velocità nel tempo
at=0
v 2 Π R 1 2Π v v
2
ac = =
Π =
= =Π ΠR
T
T
T
T
R
2
Moto parabolico
θ
Moto armonico
●
Qualitativamente moto rettilineo vario
●
Il moto armonico come "proiezione" del moto circolare uniforme su diametr0
ω → pulsazione
velocità aumenta avvicinandosi a centro di oscillazione
legge oraria x = R cos ωt
P(x,y)
O
v=?
a=?
DINAMICA
●
●
●
1a LEGGE: ogni corpo non soggetto a forza
persevera nel suo stato di quiete o di mru
a
2 LEGGE: F=ma
3a LEGGE: a ogni azione corrisponde una
reazione uguale e contraria
sistema inerziale: sistema in cui vale 1a legge; ogni
sistema che si muove con vel cost. rispetto a un sist
inerziale è anch'esso inerziale
inerzia: misura della risposta di un corpo a una forza esterna
Esempio azione-reazione
Forze azione-reazione agiscono su oggetti diversi
- LAVORO : W = F s cos θ
- POTENZA : P = W/ΔT
- ENERGIA CINETICA : K=1/2 mv2
Energia che compete a particella massiva dotata di velocità v
-TEOREMA ENERGIA CINETICA:
W = Kfin-Kin= ½ mv2fin- ½ mv2 in
-ENERGIA POTENZIALE EP= mgh
Wg = Ui-Ufin lavoro compiuto da forza di gravità su oggetto
-FORZA CONSERVATIVA se il lavoro svolto da questa forza
su particella che si muove tra due punti non dipende dalla traiettorie
Wc = Ui-Ufin
CONSERVAZIONE ENERGIA MECCANICA
●
E= K+U
Ki+Ui=Kf+Uf energia meccanica totale si conserva
per sistema isolato di oggetti che interagiscono
mediante forze conservative
●
ATTRITO?
Wnc= ΔU+ΔK
N.B. Energia totale si conserva












