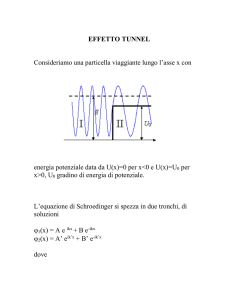
Problemi unidimensionali 1 Potenziale a gradino

Problemi unidimensionali
1
Potenziale a gradino
Studiamo una particella di energia E in presenza del potenziale unidimensionale V (x) discontinuo a
x = 0 con V0 > 0,
V (x) = 0
V (x) = V0
x≤0
x>0
(1)
Consideriamo valori differenti di E
1. 0 < E < V0 . Classicamente la particella non penetra mai nella regione con x > 0 in quanto
in questa regione l’energia totale E = p2 /2m + V0 < V0 implicherebbe un valore negativo
dell’energia cinetica p2 /2m. Per studiare il caso quantistico, scriviamo l’equazione stazionaria
di Schrödinger
p2
h̄2 d2
+ V (x)] ψ(x) = [−
+ V (x)] ψ(x) = E ψ(x)
2m
2m dx2
Per risolvere l’eq.(2) consideriamo l’intervallo x ≤ 0 (regione I) e x > 0 (regione II)
H ψ(x) = [
−
h̄2 d2
ψ(x) = E ψ(x)
2m dx2
x≤0
(2)
(3)
h̄2 d2
ψ(x) + V0 , ψ(x) = E ψ(x)
x>0
(4)
2m dx2
Risolviamo le due equazioni ed imponiamo che la funzione d’onda ψ(x) e la sua derivata prima
(ψ 0 (x)) siano continue nel punto x = 0 (condizioni di continuitá o di raccordo). Definendo
q
√
2m(V0 − E)
2mE
k1 =
k2 =
(5)
h̄
h̄
le soluzioni dell’eq.(3)-(4) si scrivono, indicando con un pedice la regione a cui si riferiscono
−
ψI (x) = A eik1 x + B e−ik1 x
ψII (x) = C ek2 x + D e−k2 x
(6)
(7)
Essendo ψ(x) finito per x → ∞ dobbiamo imporre C = 0. Imponiamo le condizioni di raccordo
ψI (x = 0) = ψII (x = 0) =⇒ A + B = D
0
ψI0 (x = 0) = ψII
(x = 0) =⇒ ik1 (A − B) = −k2 D
(8)
Notiamo che la non penetrazione della particella, come nel caso classico, richiederrebbe D = 0
che é incompatibile con una soluzione non banale. L’eq.(15) é un sistema di due equazioni
in tre incognite, che ammette sempre soluzione in termini, per esempio, della costante A.
Quest’ultima puó essere determinata dalla normalizzazione che richiederebbe lo studio di un
pacchetto d’onda. Risolvendo l’eq.(15) troviamo
B=
ik1 + k2
A
ik1 − k2
D=
Si osservi:
1
i2k1
A
ik1 − k2
(9)
(a) V0 → ∞ −→ k2 → ∞. In questo caso la discontinuitá del potenziale a x = 0 é infinita,
quindi abbiamo una sola condizione di raccordo in quanto dobbiamo imporre la continuitá
di ψ(x) e non della sua derivata
−→
ψI (x = 0) = ψII (x = 0) = 0
A+B =0
−→
A = −B
(10)
(b)
|B|2 = BB ∗ = |A|2
(11)
quindi, interpretando |A|2 e |B|2 come le probabilitá rispettivamente della funzione d’onda
della particella incidente, che avanza da sinistra sul potenziale, e della particella che torna
indietro, dalla loro uguaglianza abbiamo che la particella arriva alla barriera, penetra in
una regione di dimensione ∆x dell’ordine di k2−1 e torna indietro. Infatti nella regione II la
funzione d’onda é data da un esponenziale reale, quindi la funzione si annulla dopo essere
penetrata per un ∆x ≈ k2−1 .Dalla relazione di indeterminazione ∆k∆x ≥ 1/2 essendo ∆x
finito non siamo in grado di determinare il momento p = h̄k della particella con esatezza.
E’ evidente che l’effetto di penetrazione nella regione classicamente proibita é una conseguenza
della continuitá delle condizioni di raccordo, che vanno imposte a causa della natura ondulatoria
della particella quantistica. Mostriamo che questa proprietá non é in contraddizione con la
natura di particella, se prendiamo in conto le relazioni di indeterminazione. Come abbiamo visto
la densitá di probabilitá della particella nella regione in cui il potenziale vale V0 é apprezzabile
in un intrvallo ∆x ≈ k2−1 , ne segue che un esperimento volto a localizzare la particella nella
regione x > 0 necessariamente porta ad una indeterminazione dell’impulso
∆p ≈
q
h̄
≈ h̄k2 = 2m(V0 − E)
∆x
Di conseguenza l’energia della particella ha un’incertezza
∆E ≈
(∆p)2
≈ V0 − E
2m
quindi non é possibile affermare che l’energia della particella é piú grande E.
2. E > V0 . Classicamente la particella, se proviene da x < 0, continua nella regione con x > 0 con
la stessa energia totale,ma con minore energia cinetica in quanto vale E = p2I /2m = p2II /2m +
V0 , e non ritorna mai indietro. Nelle due regioni l’equazione stazionaria di Schrödinger, eq.(3)(4), definendo adesso
q
2m(E − V0 )
q=
(12)
h̄
ammette le soluzioni
ψI (x) = A eik1 x + AR e−ik1 x
ψII (x) = AT eiqx + D e−iqx
(13)
(14)
L’esponenziale immaginario positivo (negativo), quando consideriamo la soluzione dell’equazione
temporale di Schrödinger, descrive (rispettivamente) un’onda piano progressiva (regressiva),
2
cioé che si propaga nella direzione positiva (negativa) dell’asse x, Se supponiamo che inizialmente la particella proviene da −∞ possiamo porre D = 0 in quanto corrisponde ad una
particella proveniente da +∞. Imponiamo le condizioni di raccordo
ψI (x = 0) = ψII (x = 0)
0
ψI0 (x = 0) = ψII
(x = 0)
R=
=⇒
=⇒
k1 − q
k1 + q
1 + R=T
ik1 (1 − R) = iq2 T
T =
2k1
k1 + q
(15)
(16)
Il modulo quadro di R e T sono chiamati, rispettivamente, coefficiente di riflessione e trasmissione in quanto danno la probabitá che la particella giunta al punto di discontinuitá de potenziale venga riflessa o trasmessa. Notiamo che esiste sempre una probabilitá non nulla di riflessione
k1 − q
R=
|E→∞ −→ 0
R V0 →0 −→ 0
(17)
k1 + q
e che
k1 (1 − |R|2 ) = q |T |2
(18)
Per capire il significato fisico dell’eq.(18)studiamo l’equazione di continuitá di Schrödinger. La
corrente nelle due zone é data da
h̄
d
d
h̄k1
(ψI∗
ψI − ( ψI )∗ ψI ) =
(1 − R2 )
2m
dx
dx
m
h̄
d
h̄q 2
∗ d
jII (x) = −i
(ψII
ψII − ( ψII )∗ ψII ) =
T
2m
dx
dx
m
jI (x) = −i
(19)
(20)
Quindi possiamo interpretare l’eq.(18) come la conservazione della corrente di probabilitá
jincidente − jrif lessa = jtrasmessa
(21)
Definendo
ρ = R2 =
k1 − q
k1 + q

!2
=
1−
q
2
1+
q
 <1
1 − V0 /E
1 − V0 /E
(22)
q
4 1 − V0 /E
q 2
4k1 q
q
τ =
T| =
=
2
k1
(k1 + q)
(1 + 1 − V0 /E)2
(23)
Notiamo che ρ e τ sono invarianti per lo scambio k1 ←→ q e che vale
ρ + τ =1
con τ = 0 per V0 /E > 1 e ρ → 0 per V0 /E → 0.
3
(24)
Barriera di potenziale
L’hamiltoniana di Schrödinger per particelle di massa m in una dimensione é
H=
h̄2 d 2
px2
+ V (x) = −
+ V (x)
2m
2m d x2
(25)
Consideriamo il potenziale V (x) dato da (barriera rettangolare di potenziale)
(
V (x) =
|x| > a
|x| > a
0
VO > 0
Studiamo gli autovalori e le autofunzioni dell’hamiltoniana eq.(63) per valori dell’energia V0 > E > 0
H ψ(x) = E ψ(x)
(26)
Sostituendo l’espressione del potenziale nell’eq.(63), l’equazione di Schrödinger nelle diverse regioni
si scrive:
I) x < − a
ψI00 − k12 ψI = 0
00
II) − a < x < a
ψII
+ k22 ψII = 0
00
III) x > a
ψIII
− k12 ψIII = 0
√
2m E
k1 =
h̄
Le soluzioni delle precedenti equazioni sono
(27)
(28)
(29)
q
k2 =
2m (V0 − E)
h̄
I)
ψI = A eik1 x + B e−ik1 x
II) ψII = C e−k2 x + D ek2 x
III) ψIII = F e+ik1 x + G e−ik1 x
(30)
(31)
(32)
(33)
Se inizialmente si ha una particella che provenendo da −∞ si propaga verso destra (x crescenti),
possiamo porre G = 0 perché fisicamente non possiamo avere una particella che nella regione III,
provenendo da +∞ si propaga verso sinistra (x decrescenti). Imponendo le condizioni di continuitá
della ψ e della sua derivata prima nei punti x = ±a si ha:
ψI (x = −a) = ψII (x = −a) ⇒ Ae−ik1 a + B eik1 a = C ek2 a + D e−k2 a
(34)
0
ψI0 (x = −a) = ψII
(x = −a) ⇒ Aik1 e−ik1 a − Bik1 eik1 a = −Ck2 e+k2 a + Dk2 e−k2 a
(35)
ψII (x = a) = ψIII (x = a) ⇒ Ce−k2 a + Dek2 a = F eik1 a
(36)
0
0
ψII
(x = a) = ψIII
(x = a) ⇒ −Ck2 e−k2 a + Dek2 a = F ik1 eik1 a
(37)
4
Abbiamo un sistema di quattro equazioni in 5 incognite (A, B, C, D, F ) che ammmette sempre
una soluzione non nulla in funzione di una di esse (in seguito si sceglierá F ), da determinare successivamente dalla normalizzazione del pacchetto d’onda. Possiamo riscrivere le equazioni eq.(34) e
eq.(35) in forma matriciale
!
e−ik1 a
eik1 a
ik1 e−ik1 a −ik1 eik1 a
A
B
!
ek2 a
e−k2 a
−k2 ek2 a k2 e−k1 a
=
!
C
D
!
(38)
Moltiplicando l’eq(38) per l’inversa della matrice che appare nel lato sinistro otteniamo
A
B
!
C
D
= M (a)
!
(39)
dove M (a) é una matrice 2x2 data da

1
M (a) = 
2
1 + ikk12 eik1 a+k2 a
1 − ikk12 eik1 a−k2 a
1 − ikk12 e−ik1 a+k2 a 1 + ikk12 e−ik1 a−k2 a


Analogamente possiamo riscrivere le equazioni eq.(36) e eq.(37) nella forma
!
F
0
= M (−a)
C
D
!
(40)
Si noti che l’eq.(40) si puó ricavare immediatamente dall’eq.(38) per la simmetria del potenziale per
inversione spaziale (V (x) = V (−x), invarianza del potenziale per azione dell’operatore di paritá P,
definito da
Pψ(x) = ψ(−x)
(41)
Dall’eq.(38) e eq.(40) si ricava
!
A
B
−1
= M (a) M
(−a)
F
0
!
(42)
dove M −1 denota la matrice inversa

1
M −1 (−a) = 
2
1−
1+
ik1
k2 ik1
k2
eik1 a+k2 a 1 +
eik1 a−k2 a 1 −
ik1
k2 ik1
k2
e−ik1 a+k2 a
e−ik1 a−k2 a


Definendo le quantitá
ε=
k 2 − k12
k2 k1
−
= 2
k1 k2
k1 k2
η=
k2 k1
k 2 + k12
+
= 2
k1 k2
k1 k2
(43)
dall’eq(42) si ottiene
A = F cosh 2k2 a +
iε
2
B = F − iη2 sinh 2k2 a
5
sinh 2k2 a e2ik1 a
(44)
(45)
Il coefficiente di trasmissione τ
τ (E) = ||T ||2 = ||F/A||2 =
1
1 + (1 + ε2 /4) sinh2 2k2 a
(46)
esprime la probabilitá che una particella incidente dalla regione I sul potenziale passi attraverso la
barrriera e si propaghi nella regione III. Nel limite di barriera molta alta e/o molta lunga k2 a >> 1
l’eq.(46) si puó riscrivere, essendo
sinh 2k2 a ≈ (1/2) e2k2 a
ε2
τ (E) ≈ 1 +
4
!−1
per k2 a >> 1
16E(V0 − E) −
=
e
V02
4 e−4k2 a
√
4
(47)
2m(V0 −E)
a
h̄
(48)
da cui si ottiene, a parte fattori moltiplicativi
√
− 4
τ (E) ≈ e
2m(V0 −E)
a
h̄
(49)
Nei casi realistici il potenziale V (x) é una funzione continua, positiva e sensibilmente diversa da zero
per a < x < b. Possiamo approssimare V (x) con N barriere rettangolari di potenziale di larghezza
∆x (N ∆x = b − a) di altezza Vi = V (xi ) (i = 1, . . . , N , xi = a + i ∆x). Utilizzando l’eq.(49) si ha
τ (E) ≈
N
Y
√
− 2
e
2m(V (xi )−E)
∆x
h̄
−2
P
N
i=1
=e
√
2m(V (xi )−E) ∆x
h̄
(50)
i=1
Nel limite N → ∞, ∆x → dx si ottiene
τ (E) = e−2
√
Rd
a
2m(V (x)−E)
h̄
dx)
(51)
Si noti che nel limite ∆x → 0 l’approssimazione usata per ricavare l’eq.(49) non é piú valida. Tuttavia
si puó dimostrare con altri metodi la validitá dell’eq.(51). Nel paragrafo successivo discuteremo come
esempio di effetto tunnel il decadimento radioattivo di particelle α usando l’eq.(51).
Decadimento di particelle α
Il potenziale di una particella α (carica 2e > 0) in un nucleo di carica Ze > 0 puó essere
approssimato con un potenziale del tipo V (r) = −VO < 0 , per 0 < r < R, V (r) = 2Ze2 /r > 0
(potenziale coulombiano) per r > R, dove R é il raggio delle forze attrattive nucleari (R ≈ 10−14 m).
Trattando il problema come se fosse in una dimensione (imponendo V (x ≤ 0) → ∞) la barriera di
potenziale é descritta da
2Ze2
V (x) =
per ∞ > x > R
(52)
x
In questo caso l’integrale che appare nell’esponenziale del lato destro dell’eq.(51) diventa
√
q
√
Rb
2m(V (x)−E)
2mE R b
b
2 R
dx
=
2
dx
−1=
R
h̄
h̄
x
√
2
"
2mE
h̄
arccos
q
R
b
−
6
R
b
−
2 1/2
R
b
#
(53)
dove il limite superiore di integrazione é stato fissato imponendo che
V (x = b) = E → 2Ze2 /b = E → b = 2Ze2 /E
(54)
in quanto la trattazione che abbiamo fatto della barriera di potenziale é valida per 0 < E ≤ V (x).
Facciamo l’approssimazione b >> R ≡ E << 2Ze2 /R. Si ha
s
arccos
π
R
(b >> R) ≈ −
b
2
s
R
b
(55)
d
π
−1
π
arccos x|x=0 x = + √
|x=0 x = − x
2
dx
2
2
1−x
(56)
in quanto
arccos x (x → 0) ≈ arccos x|x=0 +
quindi, trascurando nel lato destro dell’eq.(53), il termine in (R/b)2 si ha
√
2

2mE  π
−2
h̄
2
s

R
b
(57)
Il coefficiente di trasmissione diventa quindi, inserendo il valore di b in funzione di E,
{−π
τ (E) = e
√
2m 2e2
h̄
√Z − 4
πe
E
√ ZR 2
}
(58)
Per calcolare la legge di decadimento facciamo l’approssimazione semiclassica che la probabilitá di
decadimento nell’unitá di tempo sia data dal prodotto del coefficiente di trasmissione per il numero di
urti nell’unitá di tempo nella parete della ”buca” di potenziale −V0 , cioé (u/2R) x τ (E), dove u é la
velocitá, non ben definita, della particella nel nucleo. Con questa ipotesi si deduce la legge temporale
di decadimento. In effetti il numero dN delle particelle emesse nell’intervallo di tempo t, t + dt é
dato da
dN = −N (t)xProbabilitá di decadimentoxdt
(59)
da cui si ricava, integrando
N (t) = N (0) e−t/t0
(60)
dove il tempo di vita t0 é dato da
2R
(61)
uτ
La vita media T di una sostanza che decade é definita come il tempo in cui la sostanza si é ridotta
della metá del valore iniziale
t0 =
N (t = T ) = N0 /2 = N (0) e−T /t0
→ T = t0 ln2 = 0.693t0
(62)
Con l’ipotesi fatte abbiamo ricavata una legge di decadimento che ha la corretta forma esponenziale.
L’accordo numerico con i dati sperimentali, introducendo per u un valore stimato dalla velocitá misurata delle particelle α emesse, considerando V0 dell’ordine di qualche decina di MeV, e correggendo
per un fattore numerico dovuto alle 3 dimensioni in cui avviene il proceso reale é abbastanza buono.
7
Buca di potenziale
L’hamiltoniana di Schrödinger per particelle di massa m in una dimensione é
H=
px2
h̄2 d 2
+ V (x) = −
+ V (x)
2m
2m d x2
(63)
Consideriamo il potenziale V (x) dato da (buca di potenziale)
(
V (x) =
|x| > a
|x| > a
0
− VO < 0
Studiamo gli autovalori e le autofunzioni dell’hamiltoniana eq.(63) per valori dell’energia E negativi
e maggiori del valore − V0 (V0 > |E| > 0)
H ψ(x) = E ψ(x)
(64)
Sostituendo l’espressione del potenziale nell’eq.(63), l’equazione di Schrödinger (64) nelle diverse
regioni si scrive, indicando con 1 (resp. 2) apice la derivata prima (resp. seconda) dell’autofunzione
ψ(x) rispetto a x:
I) x < − a
ψI00 − k12 ψI = 0
00
II) − a < x < a
ψII
+ k22 ψII = 0
00
III) x > a
ψIII
− k12 ψIII = 0
q
q
k1 =
2m |E|
(65)
(66)
(67)
k2 =
2m (V0 + E)
(68)
h̄
h̄
Le soluzioni delle precedenti equazioni, che si annullano all’infinito, sono
I)
ψI = A1 ek1 x
II) ψII = A2 cos k2 x + B2 sin k2 x
III) ψIII = B3 e−k1 x
(69)
(70)
(71)
Imponendo le condizioni di continuitá della ψ e della sua derivata prima nei punti x = ±a si ha:
ψI (x = −a) = ψII (x = −a) ⇒ A1 e−k1 a = A2 cos k2 a − B2 sin k2 a
(72)
0
ψI0 (x = −a) = ψII
(x = −a) ⇒ A1 k1 e−k1 a = A2 k2 sin k2 a + B2 k2 cos k2 a
(73)
−k1 a
ψII (x = a) = ψIII (x = a) ⇒ A2 cos k2 a + B2 sin k2 a = B3 e
0
ψII
(x
= a) =
0
ψIII
(x
(74)
−k1 a
= a) ⇒ −A2 k2 sin k2 a + B2 k2 cos k2 a = −B3 k1 e
(75)
Abbiamo un sistema di quattro equazioni in 4 incognite (A1 , A2 , B2 , B3 ) che ammmette soluzione
non nulla solo se il determinante della matrice M dei coefficienti delle incognite é nullo.




M =
e−k1 a
k1 e−k1 a
0
0
− cos k2 a
sin k2 a
0
−k2 sin k2 a −k2 cos k2 a
0
cos k2 a
sin k2 a −e−k1 a
−k2 sin k2 a
k2 cos k2 a k1 e−k1 a
8





Sottraendo dalla I riga la III, aggiungendo alla II la IV ed alla III la I e sottraendo dalla II la IV , si
trova


e−k1 a
−2 cos k2 a
0
e−k1 a

 k e−k1 a −2k sin k a
0
k1 e−k1 a


1
2
2

M =


e−k1 a
0
2 sin k2 a
−e−k1 a
−k1 a
−k1 a
k1 e
0
−2k2 cos k2 a −k1 e
Definendo le nuove incognite Y± = A1 ± B3 la matrice delle incognite (Y+ , A2 , B2 , Y− ) diventa:




M =
e−k1 a
−2 cos k2 a
0
0
−k1 a
k1 e
−2k2 sin k2 a
0
0
0
0
2 sin k2 a
e−k1 a
0
0
−2k2 cos k2 a k1 e−k1 a





Imponendo l’annullarsi del determinante si ha:
det |M | = 0 ⇒ 4e−2k1 a (−k2 sin k2 a + k1 cos k2 a)(k1 sin k2 a + k2 cos k2 a) = 0
(76)
Abbiamo due soluzioni
i)
ii)
k1
k2
k1
k2 cos k2 a + k1 sin k2 a = 0 ⇒ cot k2 a = −
k2
k2 sin k2 a − k1 cos k2 a = 0 ⇒ tan k2 a =
(77)
(78)
I valori discreti dell’energia tali che le eqs.(77)-(78) sono soddisfatte danno lo spettro degli stati legati
con energia < 0. Discuteremo successivamente le condizioni per le quali le equazioni trascendentali
(77) e (78) hanno soluzioni.
Supponiamo che l’eq.(77) abbia soluzione. Dalla forma della matrice diagonale a blocchi 2x2, vediamo che abbiamo ricondotto il problema a 2 sistemi di 2 equazioni a 2 incognite (Y+ , A2 ) e(B2 , Y− ).
La soluzione eq.(77) corrisponde ad una soluzione non nulla del primo sistema e alla soluzione
nulla del secondo, cioé
i) ⇒ B2 = Y− = 0 ⇒ A1 = B3
(79)
inserendo questo risultato nel primo sistema a 2 incognite
Y+ e−k1 a − A2 2 cos k2 a = 0
Y+ k1 e−k1 a − A2 2k2 sin k2 a = 0
(80)
Troviamo
e−k1 a
(81)
cos k2 a
La costante A1 é indeterminata e puó essere fisssata normalizzando la funzione d’onda, che si scriverá
A2 = A 1
I)
ψI = A1 ek1 x
II) ψII = A2 cos k2 x
III) ψIII = A1 e−k1 x
(82)
Si noti che sotto azione della paritá (x → −x) la funzione d’onda eq.(82) é invariante (funzione pari).
9
La soluzione eq.(78) corrisponde ad una soluzione nulla del primo sistema e alla soluzione non
nulla del secondo, cioé
i) ⇒ A2 = Y+ = 0 ⇒ A1 = −B3
(83)
inserendo questo risultato nel secondo sistema a 2 incognite,che scriviamo per chiarezza,
B2 2 sin k2 a + Y− e−k1 a = 0
−B2 2k2 cos k2 a + Y− k1 e−k1 a = 0
(84)
Troviamo
e−k1 a
(85)
sin k2 a
La costante A1 é indeterminata e puó essere fisssata normalizzando la funzione d’onda, che si scriverá
B2 = A1
I)
ψI = A1 ek1 x
II) ψII = B2 sin k2 x
III) ψIII = −A3 e−k1 x
(86)
Si noti che sotto azione della paritá la funzione d’onda eq.(86) cambia segno (funzione dispari). Si
noti che l’eqs.(82)-(86) soddisfano le condizioni di continuitá nei punti v ±a a causa dell’eqs.(81)-(85),
mentre le condizioni di continuitá delle derivate prime é soddisfatta dalle condizioni eqs.(77)-(78).
Discutiamo l’esistenza di soluzioni delle equazioni trascendentali. Definiamo
ξ = k2 a
η = k1 a ⇒ ξ 2 + η 2 =
2mVO a2
= R2
h̄2
(87)
L’eqs.(77)-(78) assumono la forma
ii) η = −ξ cot ξ
i) η = ξ tan ξ
(88)
Osserviamo che per l’eq.(68) e l’eq.(87) si ha che
√
0 < η, ξ < R =
2m V0
h̄
(89)
e le variabili η, ξ descrivono il primo quadrante di una circonferenza di raggio R nel piano (ξ, η). La
funzione η = ξ tan ξ é zero per ξ = 0 e la sua derivata é positiva quindi sicuramente intercetterá la
circonferenza almeno in un punto. Quindi c’é sicuramente almeno uno stato legato pari. La funzione
η = −ξ cot ξ vale - 1 per ξ = 0, la sua derivata prima é nulla per ξ = 0, cresce per 0 < ξ < π/2 ed
intercetta l’asse ξ per ξ = k2 a = π/2. Quindi puó non intercettare mai la circonferenza, sicuramente
non la intercetterá per
π2
2m V0 a2
>
(90)
4
h̄2
Possiamo descrivere gli stati legati nella tabella seguente dove abbiamo riportati lo stato fondamentale o di minima energia e gli stati eccitati in funzione del dominio di variazione del parametro ξ,
specificando anhe per ogni caso il numero di nodi, cioé di punti in cui la funzione d’onda si annulla.
Chiaramente se il valore del parametro ξ supera l’intervallo di variazione eq.(89) il corrispondente
stato legato non esiste.
10
Stato
Stato fond.
1 Stato
2 Stato
3 Stato
n-mo Stato
ξ
Simmetria N.ro nodi
[0, π/2]
Pari
0
[π/2, π]
Disari
1
[π, 3π/2]
Pari
2
[3π/2, 2π]
Dispari
3
[nπ/2, (n + 1)π/2]
(−1)n
n
Per determinare il valore dell’energia per ogni stato legato vanno risolte le equazioni trascendentali
eqs.(77)-(78), o numericamente o graficamente, determinando i valori di E = ξ 2 h̄2 /2ma2 − V0 tali
che
√ 2
R − ξ2
(91)
tan ξ =
ξ
√ 2
R − ξ2
cot ξ = −
(92)
ξ
dove R é definito in eq.(87).
2
Buca di potenziale infinita
Studiamo una particella di energia E > 0 in presenza del potenziale unidimensionale V (x) discontinuo
a x = −L, L
V (x) = 0
V (x) = ∞
|L| > |x|
|x| > |L|
(93)
Nella zona di potenziale infinito la particella non puó penetrare quindi dobbiamo imporre
|x| > |L|
ψ(x) = 0
(94)
L’equazione stazionaria di Schrödinger nella regione |x| < |L| si scrive
−
h̄2 d2
ψ(x) = E ψ(x)
2m dx2
(95)
che ammette come soluzione generale
ψ(x) = A cos kx + B sin kx
(96)
La ψ deve soddisfare le condizioni di continuitá
ψ(x = −L) = 0
ψ(x = L) = 0
(97)
che implica due tipi di soluzioni
ψP (x) = A cos kx
=⇒
k=
11
(n + 21 )π
L
n ∈ Z+
(98)
(n + 1)π
L
Le soluzioni eq.(98) si possono riscrivere nella forma (k > 0)
ψD (x) = B sin kx
ψP (x) = A cos
(kπx
2L
=⇒
k = dispari
k=
n ∈ Z+
ψD (x) = B sin f rac(kπx2L
(99)
k = pari
(100)
Si noti che per azione dell’operatore paritá definito da
P ψ(x) = ψ(−x)
(101)
Le soluzioni (98)-(99) sono autofunzioni di P rispettivamente con autovalore ±1. E’ conveniente
esprimere la condizione di annullamento delle autofunzioni in termini del numero intero
kn =
2nπ
L
n ∈ Z>
(102)
con n dispari (pari) rispettivamente per le autofunzioni pari (dispari) I corrispondenti autovalori sono
dati da
h̄2 kn2
h̄2 π 2 n2
En =
=
(103)
2m
8mL2
L’autofunzione dello stato fondamentale (n = 1) é una autofunzione pari e l’energia corrispondente
é
h̄2 π 2
(104)
E1 =
8mL2
Determiniamo le costanti A e B dalla condizione di normalizzazione
Z
L
−L
2
2
|ψ(x)| dx = |A|
L
1
cos2 kx dx = |A|2 (2L)
2
−L
Z
=⇒
1
A=B= √
L
(105)
Notiamo che:
• classicamente l’energia dello stato piú basso é 0, mentre adesso é positiva, eq.(104. La positivitá
dell’ energia dello stato fondamentale é una conseguenza del principio di indeterminazione.
Infatti essendo la particella confinata nell’intervallo finito 2L la sua indeterminazione non puó
superare questo valore, ∆x ≈ 2L, e quindi l’indeterminazione dell’impulso non puó essere nullo.
Possiamo fare una valutazione approssimata dell’energia minima. Assumendo che ∆p ≈ p, dalla
relazione d’indeterminazione tra pososizione ed impulso si ha
∆x∆p ≈≥ h̄/2
=⇒
∆p ≥
h̄
h̄
≈
2∆x
4L
(106)
quindi
E=
p2
h̄2
≥
2m
32mL2
(107)
• gli autostati non hanno una separazione in energia costante
En+1 − En =
h̄2 π 2
h̄2 π 2
2
2
[(n
+
1)
−
n
]
=
(2n + 1)
8mL2
8mL2
• il numero di nodi per ogni autofunzione 1’e n + 1.
12
(108)
3
Discussione generale
In questo paragrafo discutiamo alcune considerazioni, essenzialmente qualitative, che possono dedursi
dall’analisi dell’equazione stazionaria di Schrödinger che scriviamo nella forma
d2
2m
ψ(x) = 2 (V (x) − E) ψ(x)
2
dx
h̄
(109)
Assumiamo che V (x) sia un potenziale continuo, a corto raggio, nel senso che é non nullo in un
intervallo finito, e che ammetta un minimo Vmin .
Se V (x) − E > 0 , ψ 00 ha lo stesso segno di ψ, ne consegue che ψ é convessa rispetto all’asse x.
Se V (x) − E < 0 , ψ 00 ha il segno opposto di ψ, ne consegue che ψ é concava rispetto all’asse x.
• E < Vmin implica che V (x) − E > 0 ∀x e quindi l’eq.(109) diverge all’infinito. Quindi questo
caso non é fisicamente accettabile.
• Vmin < E < 0, in questo caso esiste uno spettro discreto di stati legati che ammette almeno un
valore. Lo spettro é non degenere e le autofunzioni ψn (n ∈ Z+ ) ammettono n nodi.
• E > 0. Nella zona in cui V (x) = 0 le soluzioni dell’eq.(109) hanno la forma rispettivamente a
sinistra e a destra
ψI (x) = eikx + R e−ikx
ψII (x) = T eikx
(110)
La soluzione nella zona in cui V (x) 6= 0 é complicata e dipende dalla forma del potenziale. La
soluzione genera e la sua derivata prima soddisfano le condizioni di continuitá. Lo spettro é
continuo con energia data da E = h̄2 k 2 /2m. In generale R 6= 0, ma esistono potenziali che cui
il coefficiente di riflessione é nullo per ogni valore dell’energia.
13