25 Il calcolo dei limiti - Il teorema del confronto

8. Il teorema dei due carabinieri
Teorema del confronto (o dei due carabinieri)
Consideriamo due funzioni f (x ) , g(x ) per le quali risulti, in un punto di accumulazione per i loro domini x 0 :
lim f (x )  lim g (x )  
x x 0
x x 0
Se abbiamo una terza funzione h(x ) per la quale risulti, in un intorno del punto x 0 , che:
f (x )  h(x )  g(x )
allora è anche:
lim h(x )  
x x 0
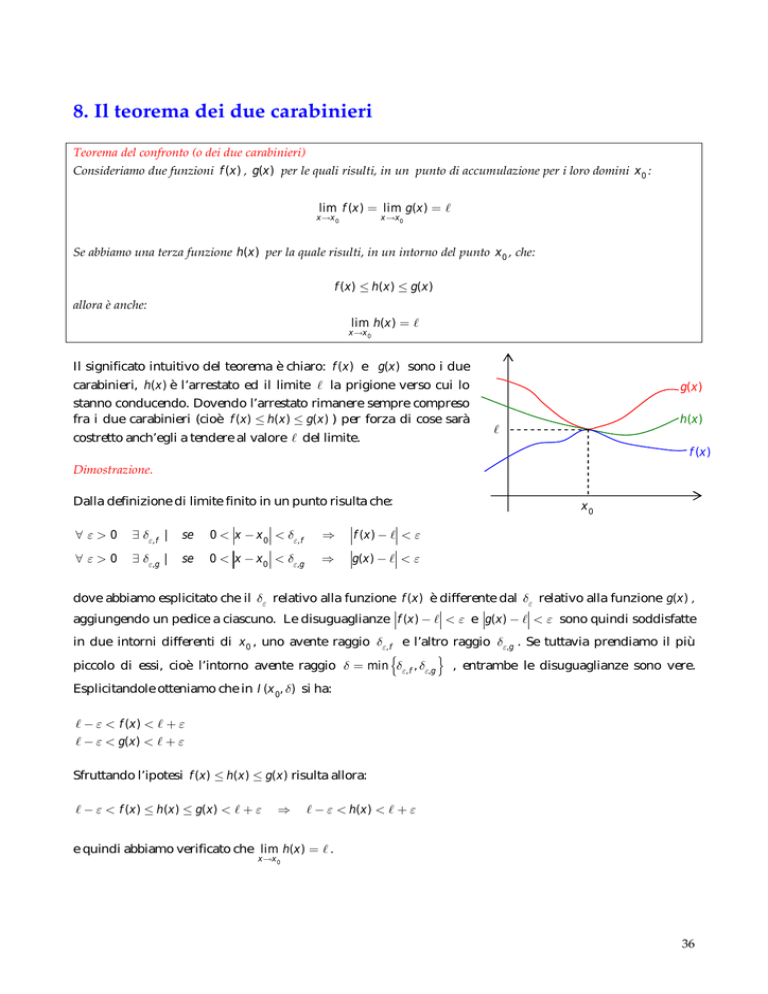
Il significato intuitivo del teorema è chiaro: f (x ) e g(x ) sono i due
carabinieri, h(x ) è l’arrestato ed il limite  la prigione verso cui lo
stanno conducendo. Dovendo l’arrestato rimanere sempre compreso
fra i due carabinieri (cioè f (x )  h(x )  g(x ) ) per forza di cose sarà
costretto anch’egli a tendere al valore  del limite.
g(x )
h (x )

f (x )
Dimostrazione.
Dalla definizione di limite finito in un punto risulta che:
 0
 , f |
se
0  x  x 0  , f

f (x )    
 0
 ,g |
se
0  x  x 0  ,g

g(x )    
x0
dove abbiamo esplicitato che il  relativo alla funzione f (x ) è differente dal  relativo alla funzione g(x ) ,
aggiungendo un pedice a ciascuno. Le disuguaglianze f (x )     e g(x )     sono quindi soddisfatte
in due intorni differenti di x 0 , uno avente raggio ,f e l’altro raggio ,g . Se tuttavia prendiamo il più

piccolo di essi, cioè l’intorno avente raggio   min , f , ,g

, entrambe le disuguaglianze sono vere.
Esplicitandole otteniamo che in I (x 0 ,  ) si ha:
    f (x )    
    g(x )    
Sfruttando l’ipotesi f (x )  h(x )  g(x ) risulta allora:
    f (x )  h (x )  g(x )    

    h(x )    
e quindi abbiamo verificato che lim h(x )   .
x x 0
36
Esempio 1
f (x )  3x 2
g(x )  5x 3
x0  0
f (x ) 0
3x 2
3
3
  lim
 lim

 
3
x 0 g(x )
x 0 5x
0 x 0 5x
0
lim
9. I limiti notevoli trigonometrici
Teorema
Si dimostra che se con x indichiamo la misura in radianti dell’angolo:
sin x
1
x 0 x
lim
Il limite si presenta evidentemente indeterminato:
lim
x 0
sin x
sin 0 0


x
0
0
ma l’indeterminazione si risolve tramite una applicazione del teorema del confronto.
sin x
Osserviamo innanzitutto che la funzione h(x ) 
è pari:
x
h(x ) 
sin(x )  sin x
sin x


 h(x )
x
x
x
il che ci consente di limitare la dimostrazione al solo caso x  0 .
Prendiamo in esame il primo quadrante della circonferenza
goniometrica. Sappiamo che una corda è sempre più corta dell’arco
che la sottende, e che il seno di un angolo e la parte di circonferenza
individuata dall’angolo sono rispettivamente metà della corda e metà
dell’arco che la sottende. Se con x indichiamo la misura in radianti
dell’angolo, vale la disuguaglianza:
tan x
sin x
x
sin x  x  tan x
Essendo nel primo quadrante sin x  0 possiamo dividere per
sin x la disuguaglianza senza che il verso ne risulti alterato:
sin x
sin x

x
1
sin x


sin x
cos
x
sin x
1
x
1

sin x
cos x
37
Passiamo ai reciproci delle quantità coinvolte. Il verso della disuguaglianza si ribalta, proprio come accade
nel seguente esempio numerico:
235

1 1 1
 
2 3 5
Si ottiene quindi:
cos x 
sin x
1
x
Possiamo applicare ora il teorema del confronto con f (x )  cos x , h(x ) 
sin x
e g(x )  1 . Dato che risulta:
x
lim cos x  1 e lim 1  1
x  0
x  0
si conclude che:
lim
x 0
Dalla parità della funzione

sin x
1
x
sin x
sin x
segue poi che è anche lim
 1.
x
x 0 x
Corollario:
E possibile anche dimostrare che se:
lim f (x )  0
x x 0
(x )
allora:
lim
x x 0
(x )
sin f (x )
1
f (x )
e
lim
x x 0
(x )
f (x )
1
sin f (x )
Esempio 1
Calcolare:
lim
x 0
sin 2x
x
Il limite si presenta indeterminato:
sin 2x
sin 0 0


x 0
x
0
0
lim
Possiamo facilmente ricondurlo al caso lim
x 0
lim
x 0
sin f (x )
con f (x )  2x moltiplicando e dividendo per 2 :
f (x )
sin 2x
sin 2x
sin 2x
 lim 2 
 2  lim
 2 1  2
x 0
x 0 2x
x
2x
38
Esempio 2
Calcolare:
lim
x 0
sin 5x
sin 3x
Il limite si presenta indeterminato:
sin 5x
sin 0 0


x 0 sin 3x
sin 0 0
lim
Moltiplichiamo e dividiamo per
lim
x 0
5x
:
3x
sin 5x
5x sin 5x
3x
5
sin 5x
3x
5
5
 lim


 lim

 11 
x 0 3x
sin 3x
5x
sin 3x
3 x 0 5x
sin 3x
3
3
Esempio 3
Calcolare:
tan x
x 0 x
lim
Il limite si presenta indeterminato:
lim
x 0
tan x
tan 0 0


x
0
0
Risolviamo:
lim
x 0
tan x
1
sin x
1
 lim

 1  1
x

0
x
cos x
x
1
Esempio 4
Calcolare:
tan 2x
x 0 sin 4x
lim
Il limite si presenta indeterminato:
tan 2x
tan 0 0


x 0 sin 4x
sin 0
0
lim
2x
:
4x
tan 2x
2x tan 2x
4x
2
1
lim
 lim


  1 1 
x 0 sin 4x
x  0 4x
2x
sin 4x
4
2
Risolviamo moltiplicando e dividendo per
39
Esempio 5
Calcolare:
lim
x 0
x  sin 2x
x  sin 3x
Il limite si presenta indeterminato:
x  sin 2x
0  sin 0
0


x 0 x  sin 3x
0  sin 0 0
lim
Risolviamo riconducendo al limite notevole del seno raccogliendo opportunamente:
 1 sin 2x 
1 sin 2x
1

2 x  

1
 2
2x 
x  sin 2x
2
2 2
2  1  3
1
2
2
x
lim
 lim
 lim
 
        
 1 sin 3x  3 x 0 1 sin 3x
 2   4 
x 0 x  sin 3x
x 0
3
1
3
4


1

3 x  
3
3x
3
3x 
3
Esempio 6
Calcolare:
x
lim e x sin x
x 0
Il limite si presenta indeterminato:
x
x

sin
x
lim e
x 0
0
0

sin
0
e
0
0
e
Risolviamo riconducendo al limite notevole del seno raccogliendo opportunamente:
x
lim e x sin x
x 0
 lim e
x
 sin x 

x 1

x 
x 0
1

 e 11
1

 e0
 e   
sin x
 1 visto che si tratta di una frazione
x
di segno positivo in cui il numeratore è sempre più piccolo del denominatore.
Dove si è fatto uso del fatto che, essendo sin x  x , allora lim
x  0
Esempio 7
Calcolare:
sin2 2x
x  0 x tan x
lim
Il limite si presenta indeterminato:
sin2 2x
sin2 0
0


x  0 x tan x
0  tan 0 0
lim
Risolviamo riconducendo al limite notevole del seno:
40
 sin 2x 2
sin2 2x
sin2 2x (2x )2
x
x
lim
 lim


 lim 
 12  4  1  4
  4x 

x 0 x tan x
x 0 (2x )2
x

0
x
tan x
tan x
 2x 
La forma indeterminata 0  
Anche l’espressione 0   risulta essere indeterminata, infatti se riscritta opportunamente si riconduce al
rapporto fra infiniti:
lim f (x )  0
e
lim g(x )  
x x 0
x x 0
risulta:
lim f (x )  g(x )  0  
x x 0
tuttavia:
f (x )  0

1

f (x )
da cui:
lim f (x )  g(x )  lim
x x 0
x x 0
g(x )


1

f (x )
Esempio 8
Calcolare:
lim x sin
x 
1
x
Il limite si presenta indeterminato:
lim x sin
x 
1
   sin 0    0
x
Riscriviamo:
lim x sin
x 
sin 1
1
x
 lim
x x  1
x
sin f (x )
1
 1 dove f (x )  soddisfa la condizione lim f (x )  0 .
x  f (x )
x 
x
Che può essere ricondotto al caso lim
Il cambio di variabile
E’ possibile a volte semplificare il calcolo di un limite attraverso l’introduzione di una variabile ausiliaria.
Vediamo un esempio.
lim
x

2
cos x


x   

2 
Il limite è indeterminato:
41

2 0
lim





      0
x 
   
x

2

2   2 2 
cos
cos x
se poniamo y  x 


, e quindi x  y  risulta che:
2
2

cos x y 

cos x
lim
 lim

y
  y 0
x 

2
x  2 
x
 

2 

2

y  0.
Sostituiamo:
  sin y 
  1
 lim 
y 0 
 y 
Teorema
Si dimostra che se con x indichiamo la misura in radianti dell’angolo:
lim
x 0
1  cos x
x
2

1
2
lim
e
x 0
1  cos x
0
x
I due limiti si presentano entrambi indeterminati:
lim
1  cos x
x 0
x
2

1  cos 0 0

0
0
1  cos x
1  cos 0 0


x 0
x
0
0
lim
Risolviamo l’indeterminazione nel primo moltiplicando e dividendo per 1  cos x :
lim
1  cos x
x 0
x2
1  cos x 1  cos x
1  cos2 x
1
sin2 x
1
1 1

 lim

 lim

 1 
2
2
2
x 0
x 0
x 0 x
1  cos x
1  cos x
1  cos x
2 2
x
x
 lim
Risolviamo il secondo:
1  cos x
1  cos x 1  cos x
1  cos2 x
1
sin2 x
1
 lim

 lim

 lim


x 0
x 0
x 0
x 0
x
x
1  cos x
x
1  cos x
x
1  cos x
lim
 lim x 
x 0
sin2 x
x
2

1
1
 0 1  0
1  cos x
2
Corollario:
E possibile anche dimostrare che se:
lim f (x )  0
x x 0
(x )
allora:
lim
x x 0
(x )
1  cos f (x )
2
f (x )

1
2
e
lim
x x 0
(x )
1  cos f (x )
0
f (x )
42
Esempio 9
Calcolare:
lim
x 0
1  cos 4x
3x
Il limite si presenta indeterminato:
1  cos 4x
1  cos 0 0


x 0
3x
0
0
lim
Riscriviamo:
lim
x 0
1  cos 4x
4 1  cos 4x
4
 lim 
 0 0
x 0 3
3x
4x
3
Esempio 10
Calcolare:
lim
x 0
1  cos x  sin x
x
Il limite si presenta indeterminato:
1  cos x  sin x
1  cos 0  sin 0 1  1  0 0



x 0
x
0
0
0
lim
Riscriviamo:
 1  cos x sin x 
1  cos x  sin x
  0  1  1
 lim 

x 0
x 0 
x
x
x 

lim
Esempio 11
Calcolare:
lim
x  0
1  cos x
x
Il limite si presenta indeterminato:
lim
x  0
1  cos x
1  cos 0
11
0



x
0
0
0
Riscriviamo considerando che x  0 quando tende a 0 :
lim
x 0

1  cos x
1  cos x
1
 lim


2
x
2
x 0
x
43
Esempio 12
Calcolare:
lim
x 0
Sapendo che lim
1  cos f (x )
2
x x 0
lim
x 0

1  cos x
x
2
f (x )
 lim

x 0

1  cos x

x
2

0
0
1
,con f (x )  x che soddisfa condizione di tendere a zero:
2
1 1  cos x
1 1


  
x
x
0 2
Esempio 13
Calcolare:
lim
1  cos x  x 2
x 0 1  3x 2
 cos x
Il limite si presenta indeterminato:
lim
1  cos x  x 2
x 0 1  3x
2
 cos x

1  cos 0  0 1  1 0


1  0  cos 0 1  1 0
Risolviamo:
1  cos x

x 2 
 1
1 1
2

1  cos x  x
 x

3 2
3
lim
 lim
 2
  

x 0 1  3x 2  cos x
x 0 2 1  cos x
1 3 2 7 7
x 
 3
2
2

 x

2
ReF sui limiti notevoli trigonometrici pp 336-338 da 208 a 238
44