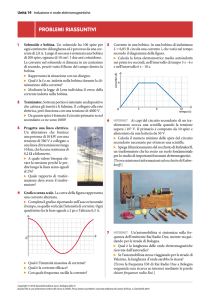
PRINCIPIO DI FUNZIONAMENTO DEL TRASFORMATORE
Il trasformatore è costituito essenzialmente da un nucleo di lamierini ferromagnetici su cui sono avvolti due
avvolgimenti in rame con diverso numero di spire (trasformatore monofase). I due avvolgimenti sono isolati fra loro
e rispetto al nucleo di ferro.
Alimentando uno degli avvolgimenti (denominato primario, con N1 spire) con una sorgente di tensione
alternata sinusoidale di valore efficace U1 si produce, per induzione elettromagnetica, una differenza di potenziale
U2 ai morsetti dell’altro avvolgimento (detto secondario e con N2 spire).
Se ai morsetti del secondario è collegato un qualsiasi utilizzatore (resistenza, motore elettrico, impianto
elettrico) questo assorbe corrente I2 ed è interessato da una certa potenza apparente data dal prodotto U2I2.
Per il principio di conservazione dell’energia (il trasformatore è considerato ancora perfetto, privo di perdite)
assorbirà dalla rete che lo alimenta al primario la stessa potenza che fluisce sul carico. In formule la potenza
apparente assorbita dalla rete è data dal prodotto U1I1 e deve essere identica alla potenza apparente sul carico
(U2I2).
In altre parole il trasformatore ha modificato esclusivamente i parametri della potenza (tensione e corrente),
ma non la potenza stessa: i ‘voltampere’ si trasferiscono dal generatore che alimenta il primario al carico allacciato
sul secondario, mentre i due circuiti, primario e secondario sono separati, isolati, non a contatto
ESEMPIO
Per il trasporto dell’energia dalla centrale il trasformatore trasferisce alla tensione U1 di 22kV la potenza S =
1000 kVA richiesta dal carico al secondario. Ma il secondario del trasformatore ha in uscita la tensione U2 di
220kV . Si calcolano
Si può notare come il trasformatore abbia elevato la tensione di 10 volte, mentre la corrente si sia ridotta di
altrettanto. Questo fatto comporta che la linea ad alta tensione adibita al trasporto dell’energia potrà essere
dimensionata per essere percorsa da una corrente 10 volte inferiore rispetto a quella assorbita dal carico e in essa
ci saranno delle perdite per effetto Joule cento volte inferiori (sono infatti legate al quadrato della corrente I2).
Nello stesso tempo la potenza in ingresso rimane la stessa di quella trasportata in uscita, a parte le perdite
interne alla macchina, qui non considerate. Nella figura è riportato lo schema del funzionamento del trasformatore.
Schema del funzionamento del trasformatore
LA TEORIA
Si alimenti ora l’avvolgimento primario con un generatore avente f.e.m. sinusoidale di pulsazione ω.
La presenza di una tensione variabile si associa al flusso le cui variazioni inducono, per induzione
elettromagnetica, una f.e.m.i. E1 ai capi delle N1 spire (autoinduzione) e parimenti una f.e.m.i. E2 ai capi
dell’avvolgimento di N2 spire (mutua induzione). Se primario e secondario sono avvolti nello stesso senso le due
f.e.m. sono tra di loro in fase, ma in ritardo di 90° rispetto al flusso inducente.
Partendo dall’ipotesi che anche il flusso sia sinusoidale e di valore istantaneo
questo, concatenandosi con le N1 spire primarie vi induce, per la legge generale dell’induzione elettromagnetica, la
f.e.m.i. primaria
in cui il flusso concatenato viene definito
Pertanto sostituendo la (3) e la (1) nella (2) si ottiene
ed essendo – cos ωt = sin(ωt – π/2) si ottiene l’espressione conclusiva
che rappresenta la f.e.m. primaria avente ampiezza
e in ritardo di π/2 rispetto al flusso induttore.
Allo stesso modo si perviene all’espressione della f.e.m. indotta ai capi delle N2 spire del secondario, sempre
in conseguenza dello stesso flusso induttore variabile (relazione (1)):
π
e2 = Eˆ 2 sin(ωt − )
2
in cui il valore massimo è
La maggiore ampiezza tra le f.e.m. primaria e secondaria dipende solo dall’avvolgimento che ha il maggiore
numero di spire (la f.e.m. indotta in ogni spira, primaria o secondaria, è ovviamente la stessa).
Nello schema riportato nella figura sottostante alla f.e.m. indotta primaria si associa il simbolo del
generatore di tensione E1 , per cui nella maglia primaria agiscono le due f.e.m. U1 ed E1 . Il valore efficace della
f.e.m. risulta, dalla (5), trattandosi di grandezza puramente sinusoidale:
In modo analogo si ricava il valore efficace della f.e.m. prodotta al secondario
Eseguendo il rapporto fra la (7) e la (8) si ottiene
in cui “n” è il rapporto spire .
Con la schematizzazione ora esaminata coincidono i moduli di U1 ed E1 e si può scrivere: