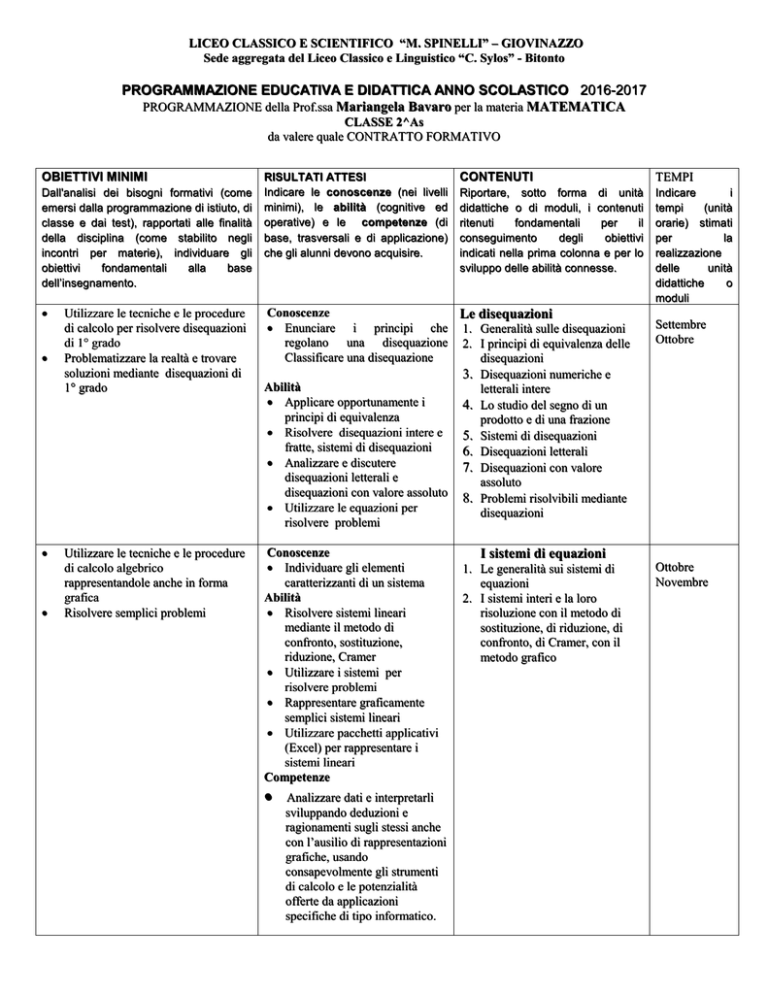
LICEO CLASSICO E SCIENTIFICO “M. SPINELLI” – GIOVINAZZO
Sede aggregata del Liceo Classico e Linguistico “C. Sylos” - Bitonto
PROGRAMMAZIONE EDUCATIVA E DIDATTICA ANNO SCOLASTICO 2016-2017
PROGRAMMAZIONE della Prof.ssa Mariangela Bavaro per la materia MATEMATICA
CLASSE 2^As
da valere quale CONTRATTO FORMATIVO
OBIETTIVI MINIMI
Dall'analisi dei bisogni formativi (come
emersi dalla programmazione di istiuto, di
c l a s s e e d a i t e s t ), ra p p o rt a t i a l l e f i n a l i t à
d e l l a d i s c i p l i n a (c o m e s t a b i l i t o n e g l i
incontri per materie), individuare gli
obiettivi
fo n d a m e n ta l i
alla
bas e
d e l l ’ i n s e g n a m e n to .
RISULTATI ATTESI
Indicare le conoscenze (nei livelli
minimi), le abilità (cognitive ed
operative) e le competenze (di
base, trasversali e di applicazione)
che gli alunni devono acquisire.
CONTENUTI
T E MP I
Riportare, sotto forma di unità
d i d a tti c h e o d i m o d u l i , i c o n te n u ti
ri t e n u t i
fo n d a m e n ta l i
per
il
c o n s e g u i m e n to
d egli
obiettivi
i n d i c a t i n e l l a p ri m a c o l o n n a e p e r l o
sviluppo delle abilità connesse.
I n d i c a re
i
te m p i
(u n i t à
o ra ri e ) s t i m a t i
per
la
realizzazione
delle
u n i tà
d i d a tti c h e
o
m oduli
Utilizzare le tecniche e le procedure
di calcolo per risolvere disequazioni
di 1° grado
Problematizzare la realtà e trovare
soluzioni mediante disequazioni di
1° grado
Conoscenze
Le disequazioni
Enunciare i principi che 1. Generalità sulle disequazioni
regolano una disequazione 2. I principi di equivalenza delle
Classificare una disequazione
disequazioni
3. Disequazioni numeriche e
Abilità
letterali intere
Applicare opportunamente i
4. Lo studio del segno di un
principi di equivalenza
prodotto e di una frazione
Risolvere disequazioni intere e
5. Sistemi di disequazioni
fratte, sistemi di disequazioni
6. Disequazioni letterali
Analizzare e discutere
7. Disequazioni con valore
disequazioni letterali e
assoluto
disequazioni con valore assoluto 8. Problemi risolvibili mediante
Utilizzare le equazioni per
disequazioni
risolvere problemi
Utilizzare le tecniche e le procedure
di calcolo algebrico
rappresentandole anche in forma
grafica
Risolvere semplici problemi
Conoscenze
Individuare gli elementi
caratterizzanti di un sistema
Abilità
Risolvere sistemi lineari
mediante il metodo di
confronto, sostituzione,
riduzione, Cramer
Utilizzare i sistemi per
risolvere problemi
Rappresentare graficamente
semplici sistemi lineari
Utilizzare pacchetti applicativi
(Excel) per rappresentare i
sistemi lineari
Competenze
Analizzare dati e interpretarli
sviluppando deduzioni e
ragionamenti sugli stessi anche
con l’ausilio di rappresentazioni
grafiche, usando
consapevolmente gli strumenti
di calcolo e le potenzialità
offerte da applicazioni
specifiche di tipo informatico.
Settembre
Ottobre
I sistemi di equazioni
1. Le generalità sui sistemi di
equazioni
2. I sistemi interi e la loro
risoluzione con il metodo di
sostituzione, di riduzione, di
confronto, di Cramer, con il
metodo grafico
Ottobre
Novembre
Utilizzare le tecniche e le procedure
di calcolo algebrico
rappresentandole in forma grafica
Risolvere semplici problemi
Conoscenze
In
un
piano
cartesiano
riconoscere punti, distanza tra
punti
Riconoscere la retta come
luogo geometrico
Conoscere
gli
elementi
caratterizzanti le equazioni
delle rette
Abilità
Classificare le rette in relazione
alla loro equazione
Rappresentare graficamente le
rette
Determinare l’equazione di rette
aventi
determinate
caratteristiche
Competenza
Utilizzare le conoscenze sulle
rette per risolvere problemi
Conoscere e utilizzare le tecniche e
le procedure di calcolo dei radicali
Saper ritrovare soluzioni a situazioni
problematiche relative ai radicali
Conoscere e utilizzare il linguaggio
simbolico dei radicali
Conoscenze
Riconosce l’ insieme di numeri
reali
Descrivere le proprietà dei
radicali
Abilità
Classifica i radicali in
aritmetici ed algebrici
Determinare l’insieme di
esistenza di un radicale
algebrico
Eseguire operazioni tra radicali
Ridurre un radicale e
trasportare un fattore fuori o
dentro il segno di radice
Ridurre espressioni irrazionali
Razionalizzare il denominatore
di una frazione
Competenza
Utilizzarein modo efficace le
proprietà dei radicali
Dicembre
Il piano cartesiano e La retta
Equazione di una retta
Fascio di rette
Retta passante per due punti
Posizione reciproca tra due rette
I radicali
1.
Le operazioni e le
espressioni con i radicali
2. Le potenze con esponente
irrazionale
3. L’insieme dei numeri reali
Gennaio
Utilizzare le tecniche e le procedure
di calcolo per risolvere equazioni e
disequazioni di 2° grado
Problematizzare la realtà e trovare
soluzioni mediante equazioni e
disequazioni di 2° grado
Utilizzare le tecniche e le procedure
di calcolo per risolvere equazioni di
grado superiore
Determinare la probabilità di un
evento
Conoscenze
Classificare le equazioni di secondo
grado
Conoscere laformula risolutiva di
una equazione di 2° grado
Abilità
Risolvere equazioni complete e non
intere e fratte
Discutere equazioni letterali
Utilizzare le equazioni per risolvere
semplici problemi
Discutere il segno delle radici
Utilizzando la regola di Cartesio
Discutere equazioni parametriche
Utilizzare pacchetti applicativi per
risolvere equazioni di 2° grado
Determinare l’intervallo di
soluzione di una disequazione intera
e/o fratta
Analizzare disequazioni di 2° grado
con valore assoluto
Competenze
Utilizzare in modo efficace una
equazione di 2° grado per risolvere
problemi anche in diversi ambiti
disciplinari
Conoscenze
Classificare le equazioni di grado
superiore al secondo
Abilità
Risolvere le equazioni binomie,
trinomie, biquadratiche, reciproche
Competenze
Utilizzare le procedure opportune
per risolvere le principali equazioni
di grado superiori al secondo
Conoscenze
Riconoscere se un evento è
certo impossibile o aleatorio
Abilità
Determinare la probabilità di un
evento
Calcolare la probabilità della
somma logica di eventi
Calcolare la probabilità del
prodotto logico di eventi
Calcolare la probabilità
condizionata
Equazioni e disequazioni di
2°grado
Equazioni di 2° grado complete e
non complete
Regola di Cartesio
Equazioni parametriche
Disequazioni di 2° grado
Equazioni e disequazioni con
valore assoluto
Equazioni di grado superiore
al secondo
Febbraio
M ar zo
Aprile
Maggio
Equazioni binomie
Equazioni trinomie
Equazioni biquadratiche
Equazioni reciproche
La probabilità di un evento
Aprile
Analizzare dati statistici,
interpretarli, sviluppare deduzioni e
ragionamenti con l’ausilio di
rappresentazioni grafiche
Conoscenze
Statistica: gli elementi
Conoscere gli elementi statistici fondamentali
Abilità
Raccogliere dati e organizzarli
Determinare la frequenza
assoluta e relativa dell’evento
Determinare gli elementi
statistici caratterizzanti i dati
statistici
Confrontare dati statistici
Rappresentare graficamente
dati statistici
Calcolare gli indici di variabilità
di una serie di dati
Conoscenza
GEOMETRIA
Riconoscere i criteri di parallelismo
1. Il parallelismo e i
Esporre sulle caratteristiche di un
parallelogrammi
parallelogramma
2. I luoghi geometrici e la
Abilità
circonferenza
Applicare i teoremi sulle rette
parallele
Dimostrare e applicare i teoremi
sui parallelogrammi
Confrontare ed analizzare i vari
parallelogrammi
Dimostrare e utilizzare i teoremi
della circonferenza
Utilizzare alcuni pacchetti
applicativi per rappresentare
figure geometriche
Competenze
Risolvere problemi
analitico-duttivo
in
modo
Ottobre
Da Dicembre a
Maggio
METODO
L’approccio alle nuove conoscenze
sarà di tipo induttivo: un problema,
una lettura che stimoli gli allievi a
porsi domande e a ricercare risposte e
soluzioni al problema. Il confronto, il
rapportare le nuove conoscenze a
quelle già acquisite sarà base di un
operare deduttivo, che guiderà
l’allievo verso la formalizzazione,
l’autonomia operativa .
Le lezioni frontali aiuteranno gli
allievi a focalizzare in modo graduale
e in modo rigoroso gli elementi teorici
fondamentali, le lezioni dialogiche a
sollecitare la partecipazione attiva dei
discenti all’attività didattica;
Ogni argomento verrà trattato con
ampia applicazione di esercizi atti a
consolidare ed estendere le nozioni
acquisite,
migliorando
contemporaneamente la padronanza
del calcolo aritmetico e algebrico;
L’uso del mezzo informatico aiuterà i
ragazzi nella formalizzazione (con
Excel) o nell’organizzazione grafica
delle conoscenze
VERIFICHE
VALUTAZIONE
La valutazione terrà conto
della partecipazione al dialogo di
classe ed alle attività di laboratorio
dell’inpegno
delle verifiche orali e scritte
Per l’accertamento di abilità e
conoscenze:
Verifiche orali La valutazione terrà
conto
della partecipazione al dialogo di
classe ed alle attività di laboratorio
dell’inpegno
- delle verifiche orali
- Verifiche scritte strutturate
e/o semistrutturate












