Università degli Studi di Bologna – II Facoltà di Ingegneria con sede a Cesena
MECCANICA APPLICATA ALLE MACCHINE L
Corso di Laurea in INGEGNERIA MECCANICA
Corso di Laurea in INGEGNERIA AEROSPAZIALE
Anno Accademico 2007-2008
II PROVA IN ITINERE (30.11.2007)
TESTO e TRACCIA di SOLUZIONE
u = penultima cifra del numero di Matricola
QUESITO No. 1
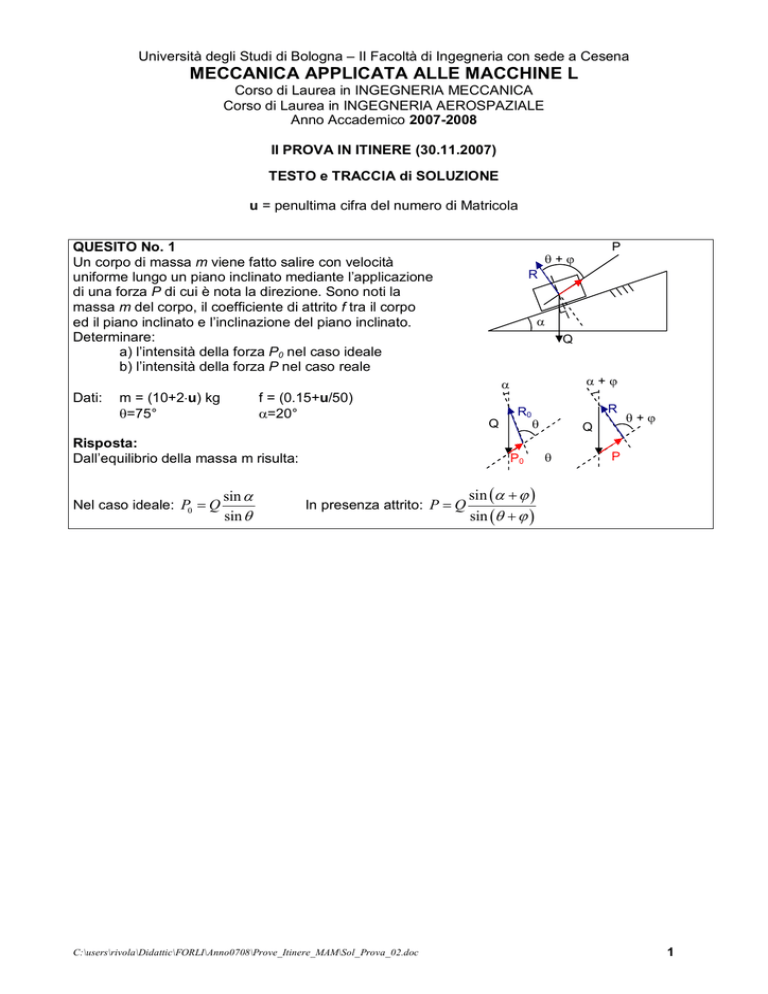
Un corpo di massa m viene fatto salire con velocità
uniforme lungo un piano inclinato mediante l’applicazione
di una forza P di cui è nota la direzione. Sono noti la
massa m del corpo, il coefficiente di attrito f tra il corpo
ed il piano inclinato e l’inclinazione del piano inclinato.
Determinare:
a) l’intensità della forza P0 nel caso ideale
b) l’intensità della forza P nel caso reale
Dati:
m = (10+2×u) kg
q=75°
f = (0.15+u/50)
a=20°
Risposta:
Dall’equilibrio della massa m risulta:
Nel caso ideale: P0 = Q
sin a
sin q
R
a
Q
a+j
a
Q
R0
R
q
P0
In presenza attrito: P = Q
C:\users\rivola\Didattic\FORLI\Anno0708\Prove_Itinere_MAM\Sol_Prova_02.doc
P
q+j
Q
q
q+j
P
sin (a + j )
sin (q + j )
1
QUESITO No. 2
Determinare l’intensità della forza P da applicare nel punto A
alla carriola di figura per farla avanzare con moto uniforme.
Il peso Q, comprendente la carriola ed il suo carico, è
concentrato nel baricentro G.
Si può trascurare l’attrito nella coppia rotoidale della ruota,
mentre si tenga conto dell’attrito volvente tra ruota e terreno
attraverso il parametro d.
Dati:
R = 200 mm
b = 400 mm
d = 10 mm
h = 800 mm
a = 600 mm
Q = 100+50×u N
K
a
b
S
Risposta:
Alla carriola sono applicate tre forze:
Q
1. La forza peso Q.
2. La reazione S del terreno sulla ruota: di cui è nota la
P
direzione (deve passare per l’asse della ruota, poiché
a
si trascura l’attrito nella coppia rotoidale, ed è spostata A
in avanti rispetto al punto teorico di contatto tra ruota e
suolo della quantità d).
G
h
3. La forza P applicata in A necessaria per equilibrare la
carriola.
Q
Per l’equilibrio alla rotazione le direzioni delle tre forze devono
passare per uno stesso punto K che si determina intersecando
a
b
le direzioni delle prime due forze. Il modulo e il verso di P si
trovano annullando la risultante delle tre forze. Costruendo il
triangolo di equilibrio e proiettando Q e P sulla normale alla
direzione di S si ottiene:
sin b
d
a
b +d
dove b = arctan e a = arctan
con d =
P sin (a + b ) = Q sin b Þ P = Q
R
d -h
tan b
sin (a + b )
d
O
R
B
d
b
QUESITO No. 3
Determinare la velocità angolare della ruota 4 del
rotismo epicicloidale a lato in cui è nota la velocità
del membro P.
Dati:
z1 = 60+u
z4 = 28
z2 = 48
z3 = 32
nP = (1000+150×u) rpm
Risposta:
Applicando la formula di Willis al rotismo ordinario equivalente si ottiene:
t0 =
zz
n4 - nP
=- 1 3
n1 - nP
z2 z4
æ
da cui, essendo n1=0, si ottiene: n4 = nP ç1 +
è
z1 z3 ö
÷
z2 z4 ø
QUESITO No. 4
In un ingranaggio conico gli assi delle due ruote formano tra di loro l’angolo g. Noto l’angolo di
semiapertura del cono primitivo della ruota 1 e la sua velocità angolare determinare la velocità
angolare della ruota 2.
Dati: g = 70°
a1 = (20+u)° n1 = (400 + 20×u) rpm
Risposta:
n
sin a1
Il rapporto di trasmissione di un ingranaggio conico vale: t = 2 =
dove a2 = g - a1.
n1 sin a 2
sin a1
È quindi immediato ricavare la velocità angolare della ruota 2: n2 = n1
sin a 2
C:\users\rivola\Didattic\FORLI\Anno0708\Prove_Itinere_MAM\Sol_Prova_02.doc
2
QUESITO No. 5
La massa m viene issata con velocità uniforme attraverso la puleggia ad
asse mobile di figura.
Indicato con d il parametro dovuto alla rigidezza della fune (di natura non
elastica) e con r il raggio del circolo di attrito della coppia rotoidale,
determinare il valore del tiro T da applicare all’estremo libero della fune.
Dati:
d = 1 mm
R = 200 mm
r = 2 mm
m = (15+2×u) kg
Risposta:
Data la natura non elastica della rigidezza alla flessione della fune i suoi
due rami tendono a disporsi come mostrato in figura.
Dall’equilibrio alla traslazione della puleggia si ottiene: T + T0 = Q
Considerando che la rotazione della puleggia è oraria il peso Q sarà
tangente a sinistra del circolo di attrito.
Dall’equilibrio alla rotazione della puleggia si ottiene:
T = kT0 con k =
1+
d
+
r
R @ 1 + 2d + 2 r
d r
R
R
1- R R
R
T =Q
k
(1 + k )
QUESITO No. 6
In una coppia rotoidale di spinta il perno è caricato da una
forza Q ed è mantenuto in rotazione uniforme attraverso
l’applicazione di un momento Mm. Conoscendo il coefficiente di
attrito f tra i due membri della coppia determinare:
a) il valore del carico Q che la coppia può sopportare;
b) il valore massimo della pressione di contatto.
Dati:
R1 = 50 mm
f = 0.3
R2 = 150 mm
Mm = 20+5×u Nm
Risposta:
Applicando al sistema l’ipotesi del Reye si ottiene: pr = C
Dall’equilibrio alla traslazione verticale: Q =
R2
ò p2p rdr =2p pr ( R
2
R1
- R1 ) Þ p =
Q
2p r ( R2 - R1 )
Il valore di Q si ottiene sostituendo l’espressione di p nell’equazione di equilibrio alla rotazione:
Mm = Q f
R1 + R2
2
da cui: Q =
2M m
f ( R1 + R2 )
Il valore massimo della pressione di contatto si ha in corrispondenza del raggio R1:
pmax =
Q
2p R1 ( R2 - R1 )
C:\users\rivola\Didattic\FORLI\Anno0708\Prove_Itinere_MAM\Sol_Prova_02.doc
3
QUESITO No. 7
In una trasmissione a cinghia piatta sono note le velocità dei due rami v1 e v2, il modulo elastico
della cinghia, l’area della sua sezione trasversale, il raggio della puleggia motrice R1 ed il tiro T1
del ramo più teso. Determinare l’intensità del momento motore M1.
Dati:
v1 = 20 m/s
S = 300 mm2
v2 = 19.5 m/s
T1 = 200×(10+u) N
E = 2×108 Pa
R1 = (150 + 10×u) mm
Risposta:
Per una trasmissione a cinghie vale la seguente relazione tra le velocità dei due rami:
v1 1 + T1 / ES
=
dalla quale è possibile ricavare il valore T2 del tiro nel ramo meno teso.
v2 1 + T2 / ES
Dall’equilibrio alla rotazione della puleggia motrice è possibile calcolare il momento motore:
M 1 = (T1 - T2 ) R1
QUESITO No. 8
Nel parallelogramma articolato di figura la manovella O1A
ruota con velocità angolare costante n.
Determinare l’intensità della forza che si scarica sul telaio
conoscendo la massa mm delle due manovelle e la massa
mb della biella.
Dati:
n = 200×(10 + u) rpm
mm = 30 g
mb = 100 g
O1A = O2B =200 mm
O1G1 = O2G2 = 10×(10 + u/2) mm
Risposta:
Dato che si tratta di un parallelogramma articolato tutti i punti della biella hanno la stessa
uuur
r
r
r
accelerazione, cioè il moto della biella è di pura traslazione. In particolare: a A = aB = aGb = -W 2 O1 A
r
uuur
r
Sulla biella agisce la forza di inerzia: Fb = - mb aGb = mb W 2 O1 A ,
mentre la coppia di inerzia è nulla (la biella trasla).
uuuur
r
r
r
La forza di inerzia che agisce su ciascuna manovella è: Fm = - mm aG1 = - mm aG 2 = mm W 2 O1G1 ,
mentre la coppia di inerzia è nulla (la velocità angolare è costante).
La forza di inerzia che si scarica a telaio è data dalla somma vettoriale delle tre forze di inerzia.
Essendo le forze parallele ed equiverse si può semplicemente sommare il loro modulo:
Ftelaio = mbW 2 (O1 A) + 2mm W 2 (O1G1 )
con W =
2p n
rad / s
60
C:\users\rivola\Didattic\FORLI\Anno0708\Prove_Itinere_MAM\Sol_Prova_02.doc
4
Università degli Studi di Bologna – II Facoltà di Ingegneria con sede a Cesena
MECCANICA APPLICATA ALLE MACCHINE L
Corso di Laurea in INGEGNERIA MECCANICA
Corso di Laurea in INGEGNERIA AEROSPAZIALE
Anno Accademico 2007-2008
II PROVA IN ITINERE (30.11.2007)
RISULTATI
penultima
cifra
matricola
0
1
2
3
4
5
6
7
8
9
penultima
cifra
matricola
0
1
2
3
4
5
6
7
8
9
Quesito 1a
[N]
Quesito 1b
[N]
Quesito 2
[N]
Quesito 3
[rpm]
Quesito 4
[rpm]
35
42
49
56
63
69
76
83
90
97
47
58
70
83
96
110
124
139
154
170
38
57
77
96
115
134
153
172
191
210
2429
2820
3219
3625
4038
4458
4886
5320
5762
6211
179
199
222
246
271
299
328
359
393
429
Quesito 5
[N]
Quesito 6a
[N]
Quesito 6b
[N/m2]
Quesito 7
[Nm]
Quesito 8
[N]
75
85
95
105
114
124
134
144
154
164
667
833
1000
1167
1333
1500
1667
1833
2000
2167
21221
26526
31831
37136
42441
47746
53052
58357
63662
68967
232
249
265
282
298
315
332
349
366
383
1140
1396
1680
1994
2339
2714
3122
3562
4036
4545
C:\users\rivola\Didattic\FORLI\Anno0708\Prove_Itinere_MAM\Sol_Prova_02.doc
5












