Esperienza diffrazione File

Università di Firenze, CdS in Fisica ed Astrofisica
Laboratorio di Ottica a.a. 2015-2016
Esperienza sulla diffrazione
Lo scopo generale dell’esperienza è la verifica delle leggi per la distribuzione angolare
dell’intensità della radiazione in uscita da una singola fenditura e da un reticolo (a grandi distanze):
singola fenditura di larghezza D (eq.1):
sin2 ⁡(𝑘𝐷
sin 𝜃)
𝐼 = 𝐼0 𝑘𝐷 2
( 2 sin 𝜃)2
reticolo con N fenditure di larghezza D e separazione a (eq.2):
sin2 ⁡(𝑘𝐷
sin 𝜃) sin2 ⁡(𝑘𝑁𝑎
sin 𝜃)
2
2
𝐼 = 𝐼0 𝑘𝐷
⁡
𝑘𝑎
( 2 sin 𝜃)2 𝑁 2 sin2 ( 2 sin 𝜃)
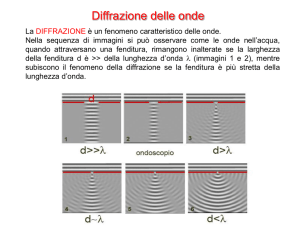
Diffrazione da singola fenditura
Si hanno a disposizione: una fenditura di larghezza D nota; una sorgente laser nel rosso (670nm);
un rivelatore CCD, con pixels quadrati di lato l6m e risoluzione sull’intensità pari ad 8 bit (281=255 livelli); un sistema di acquisizione ed un programma di analisi delle immagini. Lo scopo è di
verificare quantitativamente l’eq. 1, misurando tutti i parametri del problema.
attenuatore variabile
laser
telecamera
y
fenditura

x
Si scelga la distanza x della telecamera dalla fenditura in modo tale da rivelare sulla telecamera un
massimo secondario di intensità su entrambi i lati del massimo centrale. Nel programma di
acquisizione delle immagini, si regolino il tempo e la frequenza di acquisizione per ottimizzare la
sensibilità ed evitare saturazioni, e si controlli che il gamma factor (un esponente facoltativo per
l’intensità acquisita) sia strettamente uno. Si acquisisca quindi il profilo di intensità e si integri su
più righe della telecamera per ottenere un profilo unidimensionale I(y). Si confrontino quindi i dati
acquisiti con una funzione analoga a quella in eq.1:
sin2 (𝐵(𝑦 − 𝑦0 ))
𝐼(𝑦) = 𝐴
+𝑂
(𝐵(𝑦 − 𝑦0 ))2
sia con il “fit manuale” che con la procedura automatica di fit. Per un confronto quantitativo con
l’eq.1 vanno misurate sia x che l con relativa incertezza. Per la misurare la seconda grandezza, si
sfrutti il fatto che la riflessione del sensore della telecamera è analoga alla trasmissione di un
reticolo bidimensionale con fenditure con separazione a=l (eq.2). Per la misura si utilizzi il laser
verde fornito (532nm), e lo schema seguente.
laser
m=2
m=1
telecamera
schermo forato
Reticolo di diffrazione
Lo scopo dell’esperienza è di verificare che la posizione angolare dei massimi principali di
diffrazione segua la regola data data dall’ eq.2:
𝜆
sin 𝜃 = 𝑚 ⁡,
𝑚∈ℤ
𝑎
Per questo si studia quantitativamente la deviazione delle righe di emissione da una lampada a
Mercurio (Hg). La lampada emette principalmente a 7 diverse lunghezze d’onda nel visibile:
404.656 nm, 407.781 nm (viola), 435.835 nm (blu), 491.604 nm (verde), 546.074 nm (verde
chiaro), 576.959 nm, 579.065 nm (giallo). (attenzione: evitare di guardare a lungo l’emissione
diretta della lampada, perché contiene anche radiazione UV)
Si hanno a disposizione: un reticolo in trasmissione, con 600 linee/mm nominali (attenzione: non
toccarne la superficie perchè si danneggerebbe irremediabilmente); uno spettrogoniometro, che
permette di misurare con precisione l’angolo di deviazione della radiazione emessa da una fenditura
posta davanti alla lampada, traguardandola con un crocifilo posto sull’oculare.
spettrogoniometro
oculare
Hg

reticolo
Si ponga particolare cura nella preparazione del sistema:
a) si regoli la messa a fuoco dell’oculare guardando un oggetto all’infinito (ade esmpio fuori dalla
finestra);
b) si regoli la messa a fuoco del crocifilo sull’oculare;
c) si regoli la messa a fuoco della fenditura, e se ne aggiusti la dimensione per avere il miglior
compromesso risoluzione/visibilità;
d) si ponga il reticolo perpendicolarmente alla direzione di propagazione della luce, e si aggiusti la
base dello spettrometro in modo che la diffrazione sia orizzontale.
A questo punto, si misuri l’angolo di diffrazione come semidifferenza tra gli angoli con m=1 per
ogni riga di emissione. Se possibile, si registrino anche gli angoli di diffrazione per m=2. Per
verificare la legge del reticolo, si calcoli la spaziatura a tra le fenditure per ogni lunghezza d’onda, e
si verifichi che si ottiene in effetti un solo valore per a. Si calcoli allora la migliore stima di a
attraverso una media, e se ne verifichi la consistenza con il valore nominale.
Il setup sperimentale permette di misurare anche la dimensione della singola fenditura sul reticolo?
Eventualmente, proporre un metodo per la misura in laboratorio di questo parametro.