Matematica
Esame 19/12/16
a.a. 2016-2017
dott.ssa Rosanna Campagna
Cognome e Nome:
___________________________
Matricola:
___________________________
Istruzioni per il corretto svolgimento dell’esame:
Non è consentito l’utilizzo di appunti, fogli riassuntivi, schemi, cellulari (anche se con app
calcolatrici), … . E’ consentito l’utilizzo della calcolatrice solo se personale.
Lo studente dovrà svolgere gli esercizi scrivendo negli spazi disponibili. Non verranno corretti gli
esercizi che non riportano tale risultato. Buon lavoro.
ESERCIZI OBBLIGATORI (necessari ma non sufficienti) per il superamento dell’esame
OB_1 Descrivere l’insieme di definizione della seguente funzione:
( ) = ln(
− 2) +
−
−
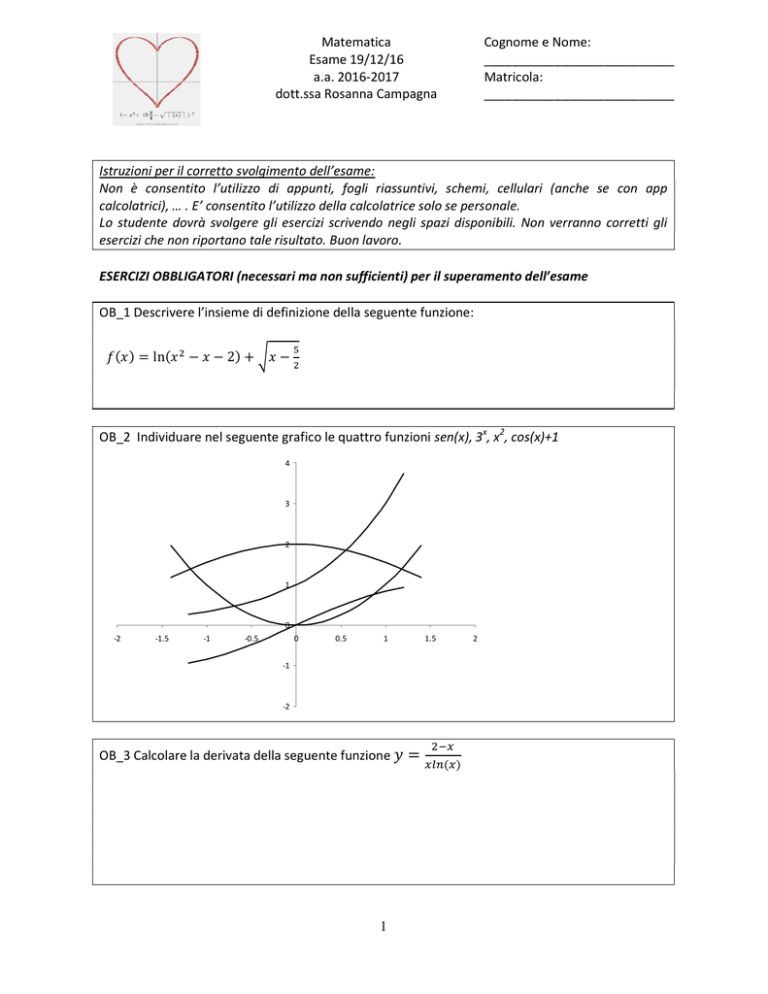
OB_2 Individuare nel seguente grafico le quattro funzioni sen(x), 3x, x2, cos(x)+1
4
3
2
1
0
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
-1
-2
OB_3 Calcolare la derivata della seguente funzione
1
=
( )
OB_4 Calcolare quanto vale il seguente limite:
lim
√
→
(
OB_5 Calcolare l’insieme delle primitive della funzione: f(x)=
OB_6 Scrivere in notazione esponenziale normalizzata
N=6022.2345
(
)
( ))
+
( )
( )
−
( )
(con 4 cifre):
R:__________________________
Scrivere in notazione esponenziale scientifica (con 4 cifre):
G=667384 x 10-16
R:__________________________
ALTRI ESERCIZI:
1. Data la funzione:
( )=
(1) specificare: dominio, intersezioni con gli assi, intervalli di positività, se è pari o dispari.
(2) Tracciare il grafico utilizzando le informazioni dedotte ed assegnando almeno 4 coppie di
punti, in un sistema di assi cartesiani.
2
2. Studiare la concavità ed individuare gli eventuali punti di flesso della funzione:
( )=6 −
2
− 5 ln ( )
3. Assegnata la funzione y= log ( +1):
a)
Descrivere il comportamento agli estremi del dominio:
b)
Quali sono gli asintoti della funzione?
c)
Esistono punti stazionari?
d)
Quali sono gli estremi assoluti?
f)
utilizzando le informazioni dedotte tracciare il grafico della funzione
4. Calcolare l’area del rettangoloide relativo alla seguente funzione nell’intervallo indicato:
( )=
/
√
in [1,4]
5. Tracciare il grafico possibile di una funzione y=f(x) date le seguenti informazioni:
Dominio [-5, 10]
3
Codominio [-3, 7]
sup f(x) 7
inf f(x) -3
Massimi relativi di f(x): 7 e 6
Punto di massimo relativo: (5/2, 6)
min rel. f(x) 5 e -3
Punto di minimo relativo: (1, 5)
Max f(x) 7
min f(x) -3
f(x) cresce in [-5, -7/2[ U ]1, 5/2[
f(x) decresce in ]-7/2,1[ U ]5/2,10[
zeri di f(x) x=6
f(x)>0 [-5, 6[
f(x)<0 ]6,10]
6. Dal grafico della funzione in
figura, determinare:
Dominio
Codominio
gli eventuali asintoti di f
estremo superiore ed estremo
inferiore
eventuali massimi e minimi relativi
gli eventuali massimi e minimi assoluti
gli intervalli in cui f cresce
gli intervalli in cui f decresce
gli intervalli in cui f >0 ed f<0
4
zeri di f
f è pari? (Si/no)
________________
f è dispari? (Si/no) ________________
7. Determina per quale valore dei parametri m e q la retta di equazione y=mx+q è tangente al
grafico della funzione = ( ) − nel punto di coordinate
,1 − .
8. Dimostrare che la funzione y=|x-x2| non è derivabile in x= 1.
9. Data la funzione ( , ) = sin (√
+ ) calcolare
F F
e
t x
10. La genetica studia la trasmissione dei caratteri ereditari, dovuta alla presenza dei cromosomi
contenuti nel nucleo di ogni cellula. Il daltonismo è una anomalia ereditaria che non consente la
distinzione di alcuni colori.
Mario è daltonico e vuole calcolare la probabilità che il bambino o bambina, che sta per avere lo
sia, sapendo che la futura mamma del nascituro non è daltonica.
Indicato con X* il cromosoma portatore dell'anomalia, geneticamente si possono presentare i
seguenti casi:
5
XY → maschio sano
X*Y → maschio daltonico
XX → femmina sana
X*X → femmina non daltonica ma portatrice sana
X*X* → femmina daltonica
Quesito 1:
Disegnare il grafo ad albero ed il quadrato di Punnet, dei casi possibili, per i figli di una coppia
formata da madre non daltonica (X*X) e padre daltonico (X*Y).
Quesito 2:
Aiuta Mario a calcolare la probabilità che nasca
•
un figlio maschio sano
•
un figlio maschio daltonico
•
una figlia femmina sana
•
una figlia femmina daltonica o non daltonica ma portatrice sana
11. Ad un paziente viene somministrato un farmaco. La funzione
8
+4
rappresenta la concentrazione del farmaco nel sangue in funzione del tempo t (tempo misurato in
ore). Calcolare dopo quanto tempo si ha la massima concentrazione del farmaco nel sangue ed a
quanto corrisponde tale concentrazione.
( )=
6












