ESEMPIO DI AMPLIFICATORE A BJT
A COLLETTORE COMUNE (EMITTER FOLLOWER)
(Dati uguali all’Esempio di par.8.3.2, Fig.8.55
del testo R.R.Spencer & M.M.Ghausi: Introduction to Electronic Circuit Design)
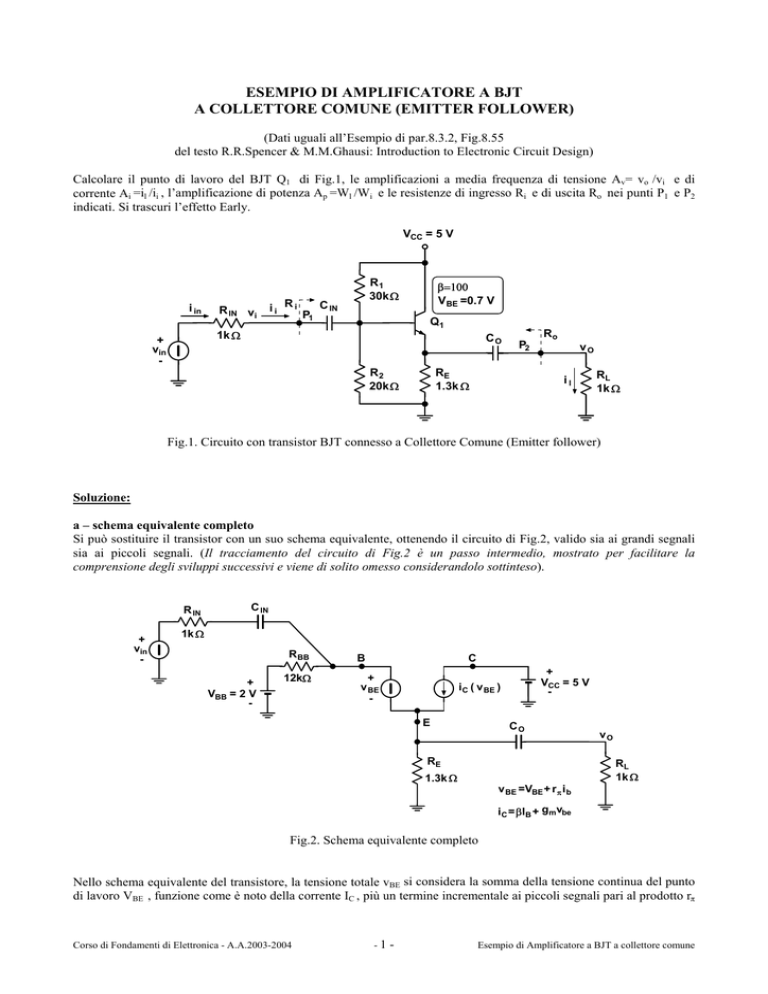
Calcolare il punto di lavoro del BJT Q1 di Fig.1, le amplificazioni a media frequenza di tensione Av= vo /vi e di
corrente Ai =il /ii , l’amplificazione di potenza Ap =Wl /Wi e le resistenze di ingresso Ri e di uscita Ro nei punti P1 e P2
indicati. Si trascuri l’effetto Early.
VCC = 5 V
i in
R IN vi
ii Ri
P1
R1
30k Ω
C IN
Q1
1k Ω
+
vin
-
β=100
VBE =0.7 V
CO
R2
20k Ω
P2
RE
1.3k Ω
Ro
vO
il
RL
1k Ω
Fig.1. Circuito con transistor BJT connesso a Collettore Comune (Emitter follower)
Soluzione:
a – schema equivalente completo
Si può sostituire il transistor con un suo schema equivalente, ottenendo il circuito di Fig.2, valido sia ai grandi segnali
sia ai piccoli segnali. (Il tracciamento del circuito di Fig.2 è un passo intermedio, mostrato per facilitare la
comprensione degli sviluppi successivi e viene di solito omesso considerandolo sottinteso).
R IN
+
vin
-
C IN
1k Ω
R BB
+
VBB = 2 V
-
12kΩ
B
C
+
v BE
-
+
VCC = 5 V
-
i C ( v BE )
E
CO
RE
vO
RL
1k Ω
1.3k Ω
v BE =VBE + r π i b
i C =βIB + gmvbe
Fig.2. Schema equivalente completo
Nello schema equivalente del transistore, la tensione totale vBE si considera la somma della tensione continua del punto
di lavoro VBE , funzione come è noto della corrente IC , più un termine incrementale ai piccoli segnali pari al prodotto rπ
Corso di Fondamenti di Elettronica - A.A.2003-2004
-1
-
Esempio di Amplificatore a BJT a collettore comune
ib . Analogamente, la corrente totale di collettore iC si considera la somma di un termine continuo, relativo al punto di
lavoro, βIB , più un termine ai piccoli segnali gm vbe .
Il partitore, formato da R1 e R2 ed alimentato da VCC , è stato sostituito dal generatore equivalente VBB e dalla
resistenza equivalente RBB . I valori di tali elementi sono dati da
VBB = VCC
R2
20 ⋅ 103
= 5⋅
=2 V
R1 + R 2
30 ⋅ 103 + 20 ⋅ 103
R BB = R 1 // R 2 =
(1)
R1 ⋅ R 2
30 ⋅ 103 ⋅ 20 ⋅ 10 3
=
= 12 kΩ
R 1 + R 2 30 ⋅ 103 + 20 ⋅ 10 3
(2)
In base al principio della sovrapposizione degli effetti, lo schema equivalente completo si può scindere in uno schema
equivalente ai grandi segnali, che consente di determinare il punto di lavoro del sistema ed in particolare del BJT, ed in
uno schema equivalente ai piccoli segnali, su cui si calcolano le amplificazioni e le impedenze richieste, che sono
appunto relative al comportamento ai piccoli segnali.
Spesso, e in particolare in questo caso, interessa il comportamento ai piccoli segnali in centro banda, cioè a frequenze
diverse dalla continua ma non troppo alte. In questo caso, di solito, i condensatori impiegati nello schema hanno valori
tali per cui le loro impedenze risultano molto alte in c. continua e abbastanza basse a frequenza di centro banda. Perciò,
se non specificato diversamente, i condensatori si considerano circuiti aperti nel ricavare lo schema ai grandi segnali e
corti circuiti nel ricavare lo schema ai piccoli segnali.
b – studio ai grandi segnali
In base a quanto detto, si osserva che, ai fini della determinazione dello schema ai grandi segnali, la parte di circuito a
monte di CIN , che comprende il generatore di corrente iin e la resistenza RIN , si può ritenere scollegata dal resto del
circuito e senza effetti. Essa viene quindi omessa. Lo schema che si ricava è mostrato in Fig.3.
R BB
+
VBB =2 V
-
VB B
12kΩ
IB
IC
+
VBE
-
C VC
+
VCC = 5 V
-
βIB
IE
E
RE
1.3k Ω
VBE = 0.7 V
Fig.3. Schema equivalente ai grandi segnali
per la determinazione del punto di lavoro
Si suppone che il BJT sia in condizioni di zona attiva e che la tensione base-emettitore sia di fatto VBE =0.7 V.
Considerando la maglia che va dalla base del BJT all’emettitore e comprende il generatore VBB , la resistenza RBB , la
caduta base-emettitore VBE e la resistenza RE , si può scrivere
VBB − R BB IB − VBE − R E IE = 0
e tenendo conto che
(3)
IC = βIB
(4)
IE = I C + IB = (β + 1) )IB
(5)
VBE = 0.7 V
(6)
si ha da (3)
Corso di Fondamenti di Elettronica - A.A.2003-2004
-2
-
Esempio di Amplificatore a BJT a collettore comune
VBB − VBE − [R BB + (β + 1)R E ] IB = 0
(7)
da cui
IB =
2 − 0.7
VBB − VBE
=
= 9.07 µA
3
R BB + (β + 1) R E 12 ⋅ 10 + (100 + 1)1.3 ⋅ 103
(8)
e quindi
I C = β IB = 100 ⋅ 9.07 ⋅ 10 −6 = 0.907 mA
(9)
IE = (β + 1) IB = (100 + 1) ⋅ 9.07 ⋅ 10 −6 = 0.916 mA
(10)
Note IC e IE , si può ricavare la tensione VCE . A tal fine si può scrivere
VC = VCC = 5 V
(11)
VE = R E IE = 1.3 ⋅ 103 ⋅ 0.916 ⋅ 10 −3 = 1.191 V
(12)
e perciò
VCE = VC − VE = 5 − 1.191 = 3.8 V
Essendo VCE >0.2 V, si conferma che il transistor è in zona attiva.
(13)
c – studio ai piccoli segnali
Dallo schema equivalente completo, azzerando i generatori in continua e quindi sostituendo i generatori di
alimentazione positiva e negativa con connessioni a massa, sostituendo il condensatore CIN con un corto circuito e
inserendo tra Base, Emettitore e Collettore lo schema equivalente del BJT ai piccoli segnali, si ottiene lo schema
equivalente ai piccoli segnali di Fig.4.
i in
R IN
1k Ω
+
vin
-
vi
ii
Ri
P1
RBB
12kΩ
vb B
ib
ic
+
vbe
-
rπ
ie
ve
ire
C vc
gmvbe
E
P2
RE
1.3k Ω
Ro
vO
il
RL
1k Ω
Fig.4. Schema equivalente ai piccoli segnali
Poiché è noto il punto di lavoro del BJT, ed in particolare è nota la corrente di collettore IC , si può determinare la
transconduttanza gm (che è un parametro ai piccoli segnali). Come è noto si ha
IC
0.907 ⋅ 10 −3
(14)
=
= 34.88 ⋅ 10 − 3 Siemens
VT
26 ⋅ 10 − 3
dove VT è la tensione termica (thermal voltage) data da VT =kT/q, con k costante di Boltzmann, T temperatura assoluta
in gradi Kelvin, q carica dell’elettrone. Essendo k=1.38066 10-23 J/ºK, q=1.60218 10-19 Coulomb, e assumendo una
temperatura di 27°C e quindi di 300°K, si ottiene VT =25.85 mV ≈ 26 mV.
gm =
Il valore della resistenza differenziale di base rπ si ricava dalla nota formula
Corso di Fondamenti di Elettronica - A.A.2003-2004
-3
-
Esempio di Amplificatore a BJT a collettore comune
rπ =
β
100
=
= 2.867 kΩ
gm 34.88 ⋅ 10 − 3
(15)
E’ conveniente trasformare lo schema equivalente ai piccoli segnali, sostituendo il circuito connesso in base con un
generatore equivalente di Thévenin, e riunendo in un’unica resistenza equivalente R’E =R’L le due resistenze in
parallelo RE e RL , come mostrato in Fig.5.
Dallo schema di Fig.4 la tensione “a vuoto” v’in, che si ottiene sconnettendo il circuito che comprende RIN , RBB ed il
generatore di tensione vin , vale
v ′in = v in ⋅
R BB
12 ⋅ 103
== v in ⋅
= v in ⋅ 0.923
R IN + R BB
1 ⋅ 103 + 12 ⋅ 103
(16)
La resistenza equivalente R’IN si ottiene nello stesso circuito annullando, cioè chiudendo in corto circuito, il generatore
di tensione vin . La R’IN è quindi data dal parallelo di RIN e di RBB
R IN R BB
1 ⋅ 103 ⋅ 12 ⋅ 10 3
=
= 923 Ω
R IN + R BB 1 ⋅ 10 3 + 12 ⋅ 103
Come detto, la resistenza equivalente R’L è data da
R ′IN = (R IN // R BB ) =
R ′E = R ′L = (R E // R L ) =
(17)
1.3 ⋅ 103 ⋅ 1 ⋅ 103
RE RL
=
= 565 Ω
R E + R L 1.3 ⋅ 103 + 1 ⋅ 103
i'in
R'IN
vb B
923 Ω
+
v'in
-
ib
(18)
ic
rπ
+
vbe
ie
ve
i'l =i e
C vc
gmvbe
E
vO
R'E =R'L
565 Ω
Fig.5. Schema equivalente ai piccoli segnali ridotto
Nello schema ridotto di Fig.5, ricordando che
ic = gm v be
ib =
(19)
ic
g
= m v be
β
β
(20)
ie = ic + ib
(21)
e quindi
ie =
β +1
β +1
ic =
gm v be
β
β
Corso di Fondamenti di Elettronica - A.A.2003-2004
(22)
-4
-
Esempio di Amplificatore a BJT a collettore comune
Considerando la maglia che comprende v’in , R’IN , base, emettitore e R’E =R’L , si può scrivere
v ′in − R ′IN ib − v be − R ′Eie = 0
(23)
Tenendo conto delle (20) e (22) si ricava
1
β +1
v ′in − gmR ′IN + 1 +
gmR ′E v be = 0
β
β
(24)
1
β +1
1
gmR ′E
1 + gmR ′IN +
β
β
e sostituendo nella (20) e nella (19)
v be = v ′in
(25)
ib = v ′in
gm
1
= v ′in
β + gm [R ′IN + (β + 1)R ′E ]
R ′IN + rπ + (β + 1)R ′E
(26)
ic = v ′in
gmβ
β
= v ′in
β + gm [R ′IN + (β + 1)R ′E ]
R ′IN + rπ + (β + 1)R ′E
(27)
ie = v ′in
gm (β + 1)
β +1
= v ′in
β + gm [R ′IN + (β + 1)R ′E ]
R ′IN + rπ + (β + 1)R ′E
(28)
Inoltre, dallo schema si ha
(β + 1)R ′E
gm (β + 1)R ′E
= v ′in
(29)
β + gm [R ′IN + (β + 1)R ′E ]
R ′IN + rπ + (β + 1)R ′E
Si può definire un’amplificazione di tensione A’v =vo /v’in , relativa allo schema ridotto, che risulta dalla (28)
v o = v e = R ′E ie = v ′in
vo
(β + 1)R ′E
gm (β + 1)R ′E
=
=
≈1
(30)
v ′in β + gm [R ′IN + (β + 1)R ′E ] rπ + R ′IN + (β + 1)R ′E
dove la semplificazione è valida soprattutto se β+1>>(rπ +R’IN )/R’E . E’ da notare che, per la connessione a collettore
comune, l’amplificazione di tensione A’v è positiva e minore ma prossima a 1.
Con i dati del caso in esame, dalla (17) si ricava
A ′v =
A ′v =
gm (β + 1)R ′E
34.88 ⋅ 10 −3 ⋅ (100 + 1) ⋅ 565
=
= 0.938
β + gm [R ′IN + (β + 1)R ′E ] 100 + 34.88 ⋅ 10 − 3 ⋅ [923 + (100 + 1) 565]
(31)
Dall’esame del circuito e dalle (25) e (29) si vede che la tensione di base vb può essere espressa da
(β + 1) R ′E
β +1
(32)
v b = v be + v e = v be 1 +
gmR ′E = v be 1 +
rπ
β
e dalle (32), (26) e (25) si ricava il rapporto rb = vb /ib , che può essere considerato come la resistenza di ingresso in base
del BJT a collettore comune. Tenendo conto anche della (15) si ottiene
[
]
vb β
=
+ (β + 1)R ′E = [rπ + (β + 1)R ′E ] = 2.867 ⋅ 10 3 + (100 + 1) ⋅ 565 = 59.932 kΩ (33)
ib
gm
Si può definire inoltre il rapporto A’i =i’l /i’in = ie /i’in come l’amplificazione di corrente relativa allo schema ridotto di
Fig.5. Dallo schema si vede che i’l =ie e che i’in =ib . Dalle (26) e (28) si ricava quindi
rb =
i
i′l
= e = (β + 1) = 101
i′in ib
L’amplificazione A’i è dunque positiva e grande.
A ′i =
(34)
E’ interessante rimarcare che lo schema ridotto di Fig.5 è lo schema tipico della connessione a emettitore comune con
resistenza di emettitore di un BJT, e che le formule (29), (34), (33) che danno le amplificazioni di corrente e di tensione
e la resistenza di ingresso, sono formule classiche riportate in tutte le tabelle.
Corso di Fondamenti di Elettronica - A.A.2003-2004
-5
-
Esempio di Amplificatore a BJT a collettore comune
E’ necessario ora tornare allo schema ai piccoli segnali completo di Fig.4 per calcolare i parametri richiesti, relativi allo
schema completo.
A questo fine è opportuno esprimere le variabili dello schema in funzione del segnale di ingresso vin anziche di v’in .
Sostituendo nelle (26), (27), (25), (29) l’espressione di v’in data dalla (16) si ottiene
ib = v in ⋅
R BB
gm
=
⋅
′
R IN + R BB β + gm [R IN + (β + 1)R ′E ]
(35)
ic = v in ⋅
R BB
gmβ
⋅
′
R IN + R BB β + gm [R IN + (β + 1)R ′E ]
(36)
v be = v in ⋅
R BB
β
⋅
′
R IN + R BB β + gm [R IN + (β + 1)R ′E ]
(37)
R BB
gm (β + 1)R ′E
R BB
⋅
= v in ⋅
⋅ A ′v
′
′
R IN + R BB β + gm [R IN + (β + 1)R E ]
R IN + R BB
inoltre, dalla (32) e dalla (37) si ricava
v o = v in ⋅
v b = v in ⋅
β + (β + 1) gmR ′E
R BB
⋅
R IN + R BB β + gm [R ′IN + (β + 1)R ′E ]
(38)
(39)
In base allo schema di Fig.4 risulta che vi =vb . Dalle (38) e (39) si ricava quindi l’amplificazione di tensione relativa
allo schema completo
vo vo
(β + 1)R ′E
gm (β + 1)R ′E
=
=
=
vi
v b β + (β + 1) gmR ′E rπ + (β + 1)R ′E
e introducendo i valori numerici
Av =
(40)
vo
gm (β + 1)R ′E
34.88 ⋅ 10 −3 ⋅ (100 + 1) ⋅ 565
(41)
= 0.952
=
=
β + (β + 1) gmR ′E 100 + (100 + 1)34.88 ⋅ 10 − 3 ⋅ 565
vi
Se si fosse voluta calcolare l’amplificazione complessiva Avt =vo /vin tra il segnale di ingresso e quello di uscita,
includendo l’attenuazione dovuta a RIN , dalla (38) e dalla (31) si può ricavare
Av =
A vt =
vo
R BB
12 ⋅ 10 3
=
⋅ A ′v =
⋅ 0.938 = 0.866
v in R IN + R BB
1 ⋅ 103 + 12 ⋅ 103
(42)
Per calcolare l’amplificazione di corrente Ai =il /ii si devono ricavare le espressioni di ii e di il in funzione delle
grandezze già determinate.
Dallo schema di Fig.4 si vede che la corrente ii =iin è data dalla somma di ib e della corrente irbb che fluisce in RBB .
Questa corrente, a sua volta, dipende dalla tensione vi =vb . Si può dunque scrivere, ricordando la definizione di rb data
dalla (33)
ii = irbb + ib =
r
vb
+ ib = ib b + 1
R BB
R BB
(43)
Ancora da Fig.4 si vede che la corrente ie =i’l si ripartisce tra le resistenze RE e RL . Come è noto, le relative correnti ire
e il stanno in proporzione inversa alle resistenze (infatti, ire =vo /RE , il =vo /RL e ie= (ire +il )). Si può dunque scrivere
RE
(44)
RE + RL
Dalle (43) e (44), tenendo conto della (34), l’amplificazione di corrente relativa allo schema completo risulta
il = ie
Ai =
il
i i i
RE
R BB
= l ⋅ b ⋅ e =
⋅
⋅ A ′i
ii ie ii ib R E + R L R BB + rb
Corso di Fondamenti di Elettronica - A.A.2003-2004
-6
-
(45)
Esempio di Amplificatore a BJT a collettore comune
e introducendo i valori numerici
Ai =
RE
R BB
1.3 ⋅ 103
12 ⋅ 10 3
⋅
⋅ A ′i =
⋅
⋅ (101) = 9.523
R E + R L R BB + rb
1.3 ⋅ 10 3 + 1 ⋅ 103 12 ⋅ 10 3 + 59.932 ⋅ 103
(46)
L’amplificazione di potenza risulta perciò
Ap =
Wl v o ⋅ il v o il
=
=
⋅ = A v ⋅ A i = (0.952 ) ⋅ (9.523) = 9.066
Wi
v i ⋅ ii
v i ii
(47)
Per calcolare la resistenza di ingresso nel punto P1 (Fig.4) si suppone di sconnettere tutta la parte esterna, cioè il
generatore di tensione vin e la resistenza RIN , di annullare nel circuito rimanente tutti i generatori indipendenti (non ve
ne sono) e di collegare in P1 un generatore di prova vx . Si ottiene la configurazione di Fig.6.
Ri
ix
+
vx
-
P1
vb B
RBB
12kΩ
ib
rπ
ic
+
vbe
ie
C vc
gmvbe
Ro
E
ve
RE
1.3k Ω
ire
vO
il
RL
1k Ω
Fig.6. Schema per il calcolo dell’impedenza di ingresso Ri .
Dallo schema, la corrente ix iniettata da vx nel punto P1 risulta
1
1
v
vx
v
1
1
+ ib = x + b = v x
+ = v x
+
R BB
R BB
rb
R BB rb
R BB rπ + (β + 1)R ′E
Poiché la resistenza Ri è per definizione Ri =vx /ix si ottiene
ix =
[
]
R [r + (β + 1)R ′E ] 12 ⋅ 103 ⋅ 2.867 ⋅ 103 + (100 + 1) 565
vx
= BB π
=
= 9.998 k Ω
ix
R BB + rπ + (β + 1)R ′E 12 ⋅ 103 + 2.867 ⋅ 103 + (100 + 1) 565
che è pari al parallelo di RBB e rb .
Ri =
(48)
(49)
In modo simile, per calcolare la resistenza di uscita nel punto P2 (Fig.4) si suppone di sconnettere tutta la parte esterna,
che in questo caso si riduce alla resistenza di carico RL , di annullare nel circuito rimanente tutti i generatori
indipendenti, cortocircuitando il generatore di segnale vin , e di collegare in P2 un generatore di prova vx . Si ottiene la
configurazione di Fig.7.
E’ evidente, dallo schema, che ix =ire −ie e che ve =vo =vx . Perciò ire =vx /RE .
Per calcolare la corrente ie causata dalla vx nell’emettitore, si osserva che a tale corrente, in base alle (19), (20), (21),
corrisponde una corrente di base ib =ie /(β+1). D’altra parte, come si vede dallo schema, una corrente ib provoca nel
parallelo di RIN e di RBB una tensione vb che vale
v b = −ib ⋅ (R IN // R BB ) = −ib
Corso di Fondamenti di Elettronica - A.A.2003-2004
1
R IN R BB
= −ie
R ′IN
β +1
R IN + R BB
-7
-
(50)
Esempio di Amplificatore a BJT a collettore comune
R IN
vi
ii
1k Ω
vb B
RBB
ib
ic
+
vbe
-
rπ
12kΩ
ie
ve
ire
C vc
gmvbe
E
P2
Ro
ix
RE
1.3k Ω
+
vx
-
Fig.7. Schema per il calcolo dell’impedenza di uscita R’o
La stessa ib provoca nella resistenza rπ una caduta
rπ
β +1
La tensione ve provocata da ie risulta quindi dalle (50) e (51)
v be = rπ ⋅ ib = ie
(51)
R′
r
R′ + r
v e = v b − v be = −ie IN + π = −ie IN π
(52)
β +1
β + 1 β + 1
Il rapporto re = −ve /ie =(R’IN +rπ )/(β+1) può essere considerato come resistenza differenziale di emettitore dello schema
di Fig.5. Come si può constatare, dall’emettitore le resistenze connesse in base vengono “viste” come se fossero ridotte
del fattore 1/(β+1).
Dalle relazioni precedenti si ha
1
vx
β +1
β +1
+ ve
= v x
+
RE
R ′IN + rπ
R E R ′IN + rπ
La resistenza di uscita Ro per definizione è quindi
i x = ire − ie =
Ro =
R E (R ′IN + rπ )
vx
1
=
=
′
ix
R
1
β +1
IN + rπ + (β + 1)R E
+
R E R ′IN + rπ
(53)
(54)
che è il parallelo di RE con re .
Sostituendo i valori dei parametri si ha
(
)
R E (R ′IN + rπ )
1.3 ⋅ 103 923 + 2.867 ⋅ 103
(55)
=
= 36.472 Ω
R ′IN + rπ + (β + 1)R E 923 + 2.867 ⋅ 103 + (100 + 1)1.3 ⋅ 10 3
Il risultato ottenuto conferma che la connessione a collettore comune è caratterizzata da una bassa resistenza di uscita.
Si può osservare che, nel caso si fosse dovuto tener conto dell’effetto Early, si sarebbe dovuta definire una
corrispondente resistenza ro in parallelo al generatore di corrente comandato gm vbe nello schema equivalente ai piccoli
segnali del BJT. L’effetto di tale resistenza è normalmente trascurabile nel calcolo dei parametri considerati in questo
esercizio. Per la connessione a collettore comune, ciò vale anche nella determinazione della resistenza di uscita Ro.
Ro =
Corso di Fondamenti di Elettronica - A.A.2003-2004
-8
-
Esempio di Amplificatore a BJT a collettore comune